min25筛详解+如何推式子+杜教筛

Part.1 min25筛

前情提要：应用特别广泛，代码难度一般，但理解难度较大

若f(i)为积性函数

求 $\sum_{i=1}^nf(i)$

主要思路就是将积性函数分为三个部分来求和，当 i 是质数，当 i 是合数，还有i等于1

它的思想类似DP

首先需要了解一下埃氏筛法（圈一个质数，划去它的倍数）

我们先不考虑1

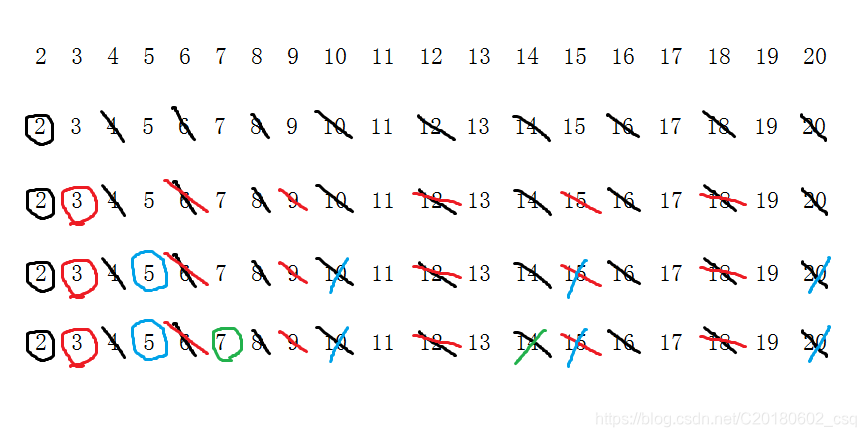
先来考虑如何表示一个埃氏筛的状态

我们可以从筛子的范围与所圈质数的个数来表示一个筛子

设g[n][k]表示筛子的范围为2~n，用前k个质数来筛，最后没有被叉掉的数的 f 值之和

怎么转移？

考虑埃氏筛的过程，选定一个质数后，直接从它的平方开始筛

所以当Pk*Pk>n时，g[n][k]=g[n][k-1] （Pk是第k个质数）

否则我们就一定会再叉掉一些数，减掉一部分f值

$g[n][k]=g[n][k-1]-f(P_k)*(g[\left \lfloor \frac{n}{P_k} \right \rfloor][k-1]-g[P_k-1][k-1])$

这里利用了f是积性函数的条件

$f(P_k)*g[\left \lfloor \frac{n}{P_k} \right \rfloor][k-1]$

理解：用前k-1个质数来筛，把没筛掉的数，作为Pk的倍数（这个倍数一定会前k-1个质数互质）（当然，这个倍数*Pk应该小于n）来确定Pk需要筛哪些点。由于前k-1个质数也是剩下的数，所以还要加上（就是 $f(P_K)*\sum_{i=1}^{k-1}f(P_i)$ ，即Pk与前k-1个质数的组合）

注意：由于我们是要求i为质数是f值之和，所以我们一开始应该把所有数都当成质数

（具体实现后面再讲）

我们已经完成了第一步

第二步就是求出合数部分的答案

其实我们已经可以直接求所有数（除1以外）的答案了

设s[n][k]表示筛的范围为2~n，用了前k-1个质数来筛，剩下的数的 f 值之和（除去前k-1个质数的f值）

（感觉跟g的定义一模一样？其实不是，s求的是真正的答案，而g是把所有的数当成质数来算的答案）

（而且g是去掉了Pk筛掉的合数，s包含了Pk筛掉的合数，但又要去掉前k-1个质数的答案）

同理Pk*Pk>n时，s[n][k]=s[n][k-1]-f(P_{k-1})

我们明显知道当 $P_{k+1}*P_{k+1}>n$ 且时（筛的临界点），再让 $P_{k+1}$ 来筛已经没有意义了，即剩下的都是质数了

所以此时的s[n][k]就是g[n][k]-f(P1)-f(P2)-...-f(P_{k-1})

为了方便，我们把这个临界点的k值即为 |P|

于是我们有转移：

$s[n][k]=g[n][|P|]-\sum_{i=1}^{k-1}f(P_i)+\sum_{i=k}^{P_i^2<=n}\sum_{j=1}^{P_i^{j+1}<=n} (f(P_i^j)*s[\left \lfloor \frac{n}{P_i^j} \right \rfloor][i+1]+f(P_i^{j+1}))$

我们现在相当于在执行筛质数的逆过程，即用质数组合出合数的过程

我们可以写出一个等价的状态定义：s[n][k]表示用第k~|P|的质数，组合出的数（包括质数本身）的 f 值之和

注意：这里新组合的数指的是将最小质因子大于等于Pk的数

理解：

$g[n][|P|]-\sum_{i=1}^{k-1}f(P_i)$ 在单独计算质数的答案

$f(P_i^j)*s[\left \lfloor \frac{n}{P_i^j} \right \rfloor][i+1]$

枚举当前质数Pi，以及它的幂次j，作为最小质因子，用与前k个质数互质的数来作为他的倍数，

求出曾经被它叉掉的（即以它作为最小质因子，新组合出来的）数的 f 值之和

由于这样只能求它与其他质数组合出的合数的答案

所以我们还要加上 $f(P_i^{j+1})$ ，让他自己和自己也可以组合出合数

最后加上f(1)的答案就好啦

时间复杂度？ $O(n^{1-\epsilon })$ (差不多线性)，但是在n比较小的情况下是 $O(\frac{n^{\frac{3}{4}}}{logn})$

具体实现：

拿一道例题来讲

最小公倍数计数

定义F(n)表示最小公倍数为n的二元组的数量。

即：如果存在两个数（二元组）X，Y(X <= Y)，它们的最小公倍数为N，则F(n)的计数加1。

例如：F(6) = 5，因为(2,3)(1,6)(2,6)(3,6)(6,6)的最小公倍数等于6。

给出一个区间a,b，求最小公倍数在这个区间的不同二元组的数量。

例如：a = 4，b = 6。符合条件的二元组包括：(1,4)(2,4)(4,4)(1,5)(5,5)(2,3)(1,6)(2,6)(3,6)(6,6)，共10组不同的组合。

Input

输入数据包括2个数：a, b，中间用空格分隔（1 <= a <= b <= 10^11)。

Output

输出最小公倍数在这个区间的不同二元组的数量。

Sample Input

4 6

Sample Output

~~很明显，F是一个积性函数~~

差分一下，求F的前缀和

转换一下，我们先来计算有序对的个数

为了方便，我们把p都当成是质数

F(p)=3，因为只可能有(1,p)(p,1)(p,p)三种组合

F(p^c)=2c+1，因为我们必须将其中一个数固定为p^c才可以让lcm取到p^c，剩下一个数有c+1种取值（1,p,p^2,p^3....p^c）

但由于两个数同时取p^c的情况被重复计算了，所以要减1

F(ab)，当a，b互质时，显然有F(ab)=F(a)*F(b)，即分开组合a与b

于是我们就把问题转换为了求积性函数F的前缀和

先放上套路式：

$g[n][k]=g[n][k-1]-f(P_k)*(g[\left \lfloor \frac{n}{P_k} \right \rfloor][k-1]-\sum_{i=1}^{k-1}f(P_i))$

$s[n][k]=g[n][|P|]-\sum_{i=1}^{k-1}f(P_i)+\sum_{i=k}^{P_i^2<=n}\sum_{j=1}^{P_i^{j+1}<=n} f(P_i^j)*s[\left \lfloor \frac{n}{P_i^j} \right \rfloor][i+1]$ $+f(P_i^{j+1})$

首先，我们发现n的取值只有 $\sqrt{n}$ 种（因为每次只调用了 $\left \lfloor \frac{n}{x} \right \rfloor$ 作为下标（ $\left \lfloor \frac{\left \lfloor \frac{n}{x} \right \rfloor}{y} \right \rfloor=\left \lfloor \frac{n}{xy} \right \rfloor$ ））

于是可以把这些位置预处理出来，n*k --> sqrt(n)*k

for(i=1;i<=n;i=j+1){
    	j=n/(n/i);
    	a[++m]=n/i;
    	if(a[m]<=T)id1[a[m]]=m;//小于根号n
        else id2[n/a[m]]=m;
}

由于当前状态只与k-1有关，g[n]可以原地转移，省去k，sqrt(n)*k --> sqrt(n)

然后把g[n]在k=0时的值（相当于把所有数当成质数，求前缀和）预处理出来

for(i=1;i<=n;i=j+1){
        j=n/(n/i);
        a[++m]=n/i;
        if(a[m]<=T)id1[a[m]]=m;
        else id2[n/a[m]]=m;
        g[m]=3ll*(a[m]-1);
}

计算出k=|P|时的g数组

#define id(i) (((i)<=T)?id1[i]:id2[n/(i)])
for(j=1;j<=tot;j++)
	for(i=1;i<=m&&prime[j]*prime[j]<=a[i];i++)
		g[i]-=g[id(a[i]/prime[j])]-3ll*(j-1);

此时a[i]存的是位置 i 的实际取值（a是降序），id(x)求的是实际取值x对应的位置

先要线性筛一下质数，筛到sqrt(n)即可

枚举当前质数prime[j]，再枚举它可以让哪些取值 a[i] 发生转移

由于a[i]越小越不容易转移，所以当第一个a值不满足时，后面的都已经不满足了，也不用转移了

（原地转移：不转移等价于g[n][k]=g[n][k-1]）

3ll*(j-1) 就是在计算 $\sum_{i=1}^{j-1}f(P_i)$

s[n][k]部分的计算就比较好理解了（递归计算）（直接套式子）

$s[n][k]=g[n][|P|]-\sum_{i=1}^{k-1}f(P_i)+\sum_{i=k}^{P_i^2<=n}\sum_{j=1}^{P_i^{j+1}<=n} f(P_i^j)*s[\left \lfloor \frac{n}{P_i^j} \right \rfloor][i+1]$ $+f(P_i^{j+1})$

LL solve(LL a,LL b)//s[a][b]
{
	if(a<prime[b]) return 0;
	LL ans=g[id(a)]-3ll*(b-1);
	for(LL i=b;i<=tot&&1ll*prime[i]*prime[i]<=a;i++)
		for(LL j=1,p=prime[i];p*prime[i]<=a;j++,p*=prime[i])
			ans+=solve(a/p,i+1)*(2*j+1)+(2*(j+1)+1);
	return ans;
}

完整代码：

#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 1000000
#define LL long long
#define id(i) (((i)<=T)?id1[i]:id2[n/(i)])
LL prime[N],id1[N],id2[N],tot;
bool vis[N];
LL g[N],a[N],T,n,m;
void min25()
{
	tot=m=0;T=sqrt(n+0.5);
	LL i,j;
	for(i=2;i<=T;i++){
		if(!vis[i])prime[++tot]=i;
		for(j=1;j<=tot&&1ll*i*prime[j]<=T;j++){
			vis[i*prime[j]]=1;
			if(i%prime[j]==0)break;
		}
	}
	for(i=1;i<=n;i=j+1){
		j=n/(n/i);
		a[++m]=n/i;
		if(a[m]<=T)id1[a[m]]=m;
		else id2[n/a[m]]=m;
		g[m]=3ll*(a[m]-1);
	}
	for(j=1;j<=tot;j++)
		for(i=1;i<=m&&prime[j]*prime[j]<=a[i];i++)
			g[i]-=g[id(a[i]/prime[j])]-3ll*(j-1);
}
LL solve(LL a,LL b)
{
	if(a<prime[b]) return 0;
	LL ans=g[id(a)]-3ll*(b-1);
	for(LL i=b;i<=tot&&1ll*prime[i]*prime[i]<=a;i++)
		for(LL j=1,p=prime[i];p*prime[i]<=a;j++,p*=prime[i])
			ans+=solve(a/p,i+1)*(2*j+1)+2*(j+1)+1;
	return ans;
}
LL sum(LL x)
{
	if(x<=0)return 0;
	if(x==1) return 1;
	n=x;min25();
	return (solve(x,1)+1+n)/2ll;
}
int main()
{
	LL a,b;
	scanf("%lld%lld",&a,&b);
	printf("%lld",sum(b)-sum(a-1));
}

Part.2 推式子的具体方法

前情提要：《具体数学》第2章的个人理解

做数论题的关键就是列出正确的式子，真正的题是不会像这种题一样板的

如何列出正确的式子呢？

额……这个不太好说吧。。。具体问题具体分析，找规律，补集转换，容斥原理（一般都有一些数量上限制）

当我们列出了正确的式子，就可以来推它了。。。

当然，在推导之前，也要看一下式子的含义，分析问题的本质（大力质因数分解）

（Freopen大佬有云：如果你一来就推式子，那么你已经输了）

所以分析很重要

顺便讲一下推式子的技巧

1、求和号

可能一开始入手数论的时候不太懂

当两个求和号没有任何关联时，我们就可以直接交换它们

$\sum_{i=1}^{n}\sum_{j=1}^nf(i)*f(j)=\sum_{j=1}^n\sum_{i=1}^{n}f(i)*f(j)$

如果求和的值(f(i)、f(j))与求和号指标(i、j)无关（如f(i)与j无关,f(j)与i无关）

那么就可以把里面的值提出来（如果有关就不能提出来了）

$\sum_{i=1}^n\sum_{j=1}^nf(i)*f(j)=\sum_{i=1}^n(f(i)*\sum_{j=1}^nf(j))=(\sum_{i=1}^nf(i))*(\sum_{j=1}^nf(j))$

如果求和号的指标之间有关怎么办？

我们在交换求和号的时候就要有一个原则：

让每个指标都可以取到自己原来可以取到的值，并且它们之间的关系不变

如： $\sum_{i=1}^{n}\sum_{j=1}^{i}f(i)*f(j)$

i,j是可以取到n的，i>=j

所以交换求和号之后是：

$\sum_{j=1}^{n}\sum_{i=j}^{n}f(i)*f(j)$

再来一个

$\sum_{i=1}^n\sum_{d|i}f(i)*f(d)$ （ $\sum_{d|i}$ 表示枚举i的约数d）

i,d都是可以取到n的，并且d|i

所以交换后就是：

$\sum_{d=1}^n\sum_{d|i}^nf(i)*f(d)$ （ $\sum_{d|i}^n$ 表示枚举d的倍数i，且i<=n）

如果实在无法理解，你可以自己尝试把求和的值列成一个矩阵，然后把按行求和换成按列求和来体会一下

多个求和号？两个两个地交换就是了，虽然慢了点，但是不容易错

2、换元

我们一般会把枚举倍数的求和形式

$\sum_{d=1}^n\sum_{d|i}^nf(i)*f(d)$

换成

$\sum_{d=1}^n\sum_{i=1}^{\left \lfloor \frac{n}{d} \right \rfloor}f(i*d)*f(d)$

其实就是令 i'=i/d，就可以把后面的所有 i 换成 i'*d，很明显 i' 的取值只有 $\left \lfloor \frac{n}{d} \right \rfloor$ 个

换元的运用远不止这些。。。

3、推式子推到一定程度就可以了，能够直接求和就直接求了，不行就考虑杜教筛，min_25筛，暴力筛……

4、 $[x=1]=\sum_{i|x}\mu(i)$

(莫比乌斯函数的性质，一般都用这个，其实它本质就是狄利克雷卷积式子 $\epsilon =1*\mu$ )

(莫比乌斯反演的狄利克雷卷积形式就是 $f*1=g\Leftrightarrow f=g*\mu$ )

Part.3 杜教筛的使用方法

前置技能：了解狄利克雷卷积

求：

$S(n)=\sum_{i=1}^ni^2*\varphi(i)$

设f(i)=i*i*phi(i)

写成狄利克雷卷积形式：

$id\cdot id\cdot \varphi$

消掉id^2，让他卷一个id^2（设g=id^2）

$(id\cdot id\cdot \varphi)*(id\cdot id)$

写回来（狄利克雷卷积的第 i 项）

$\sum_{d|i}d*d*\varphi(d)*\frac{i}{d}*\frac{i}{d}$

$=i^2\sum_{d|i}\varphi(d)$

因为 $\varphi*1=id$

所以：

求个和

$\sum_{i=1}^n(f*g)(i)=\sum_{i=1}^ni^3$

展开左边

$\sum_{i=1}^n\sum_{d|i}f(\frac{i}{d})*g(d)=\sum_{i=1}^ni^3$

$\sum_{d=1}^n\sum_{d|i}^{n}f(\frac{i}{d})*g(d)=\sum_{i=1}^ni^3$

$\sum_{d=1}^n\sum_{i=1}^{\left \lfloor \frac{n}{d} \right \rfloor}f(i)*g(d)=\sum_{i=1}^ni^3$

$\sum_{d=1}^ng(d)*\sum_{i=1}^{\left \lfloor \frac{n}{d} \right \rfloor}f(i)=\sum_{i=1}^ni^3$

把第一项单独列出来

$g(1)*\sum_{i=1}^nf(i)+\sum_{d=2}^ng(d)*\sum_{i=1}^{\left \lfloor \frac{n}{d} \right \rfloor}f(i)=\sum_{i=1}^ni^3$

把f(1)+f(2)+...+f(n)换成S(n)

$g(1)*S(n)+\sum_{d=2}^ng(d)*S(\left \lfloor \frac{n}{d} \right \rfloor)=\sum_{i=1}^ni^3$

最后：

$g(1)*S(n)=\sum_{i=1}^ni^3-\sum_{d=2}^ng(d)*S(\left \lfloor \frac{n}{d} \right \rfloor)$

$S(n)=\sum_{i=1}^ni^3-\sum_{d=2}^nd^2*S(\left \lfloor \frac{n}{d} \right \rfloor)$

发表于 2020-01-15 09:37 cqbzcsq 阅读(467) 评论(0) 收藏举报

刷新页面返回顶部

min25筛详解+如何推式子+杜教筛

Part.1 min25筛

最小公倍数计数

Part.2 推式子的具体方法

Part.3 杜教筛的使用方法

公告

导航