EM算法原理
转自:https://www.cnblogs.com/Gabby/p/5344658.html
我讲EM算法的大概流程主要三部分:需要的预备知识、EM算法详解和对EM算法的改进。
一、EM算法的预备知识
1、极大似然估计
(1)举例说明:经典问题——学生身高问题
我们需要调查我们学校的男生和女生的身高分布。 假设你在校园里随便找了100个男生和100个女生。他们共200个人。将他们按照性别划分为两组,然后先统计抽样得到的100个男生的身高。假设他们的身高是服从高斯分布的。但是这个分布的均值u和方差∂2我们不知道,这两个参数就是我们要估计的。记作θ=[u, ∂]T。
问题:我们知道样本所服从的概率分布的模型和一些样本,而不知道该模型中的参数。

我们已知的有两个:(1)样本服从的分布模型(2)随机抽取的样本 需要通过极大似然估计求出的包括:模型的参数
总的来说:极大似然估计就是用来估计模型参数的统计学方法。
(2)如何估计
问题数学化: (1)样本集X={x1,x2,…,xN} N=100 (2)概率密度:p(xi|θ)抽到男生i(的身高)的概率 100个样本之间独立同分布,所以我同时抽到这100个男生的概率就是他们各自概率的乘积。就是从分布是p(x|θ)的总体样本中抽取到这100个样本的概率,也就是样本集X中各个样本的联合概率,用下式表示:
这个概率反映了,在概率密度函数的参数是θ时,得到X这组样本的概率。 需要找到一个参数θ,其对应的似然函数L(θ)最大,也就是说抽到这100个男生(的身高)概率最大。这个叫做θ的最大似然估计量,记为
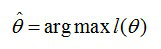
(3)求最大似然函数估计值的一般步骤
首先,写出似然函数:
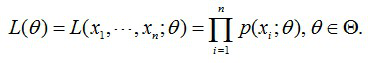
其次,对似然函数取对数,并整理:
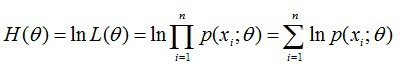
然后,求导数,令导数为0,得到似然方程;
最后,解似然方程,得到的参数即为所求。
(4)总结
多数情况下我们是根据已知条件来推算结果,而极大似然估计是已经知道了结果,然后寻求使该结果出现的可能性最大的条件,以此作为估计值。
2、Jensen不等式
(1)定义
设f是定义域为实数的函数,如果对于所有的实数x。如果对于所有的实数x,f(x)的二次导数大于等于0,那么f是凸函数。 Jensen不等式表述如下: 如果f是凸函数,X是随机变量,那么:E[f(X)]>=f(E[X]) 。当且仅当X是常量时,上式取等号。
(2)举例

图中,实线f是凸函数,X是随机变量,有0.5的概率是a,有0.5的概率是b。X的期望值就是a和b的中值了,图中可以看到E[f(X)]>=f(E[X])成立。 Jensen不等式应用于凹函数时,不等号方向反向。
二、传统EM算法详述
1、问题描述
我们抽取的100个男生和100个女生样本的身高,但是我们不知道抽取的那200个人里面的每一个人到底是从男生的那个身高分布里面抽取的,还是女生的那个身高分布抽取的。 用数学的语言就是,抽取得到的每个样本都不知道是从哪个分布抽取的。 这个时候,对于每一个样本,就有两个东西需要猜测或者估计: (1)这个人是男的还是女的?(2)男生和女生对应的身高的高斯分布的参数是多少?
EM算法要解决的问题是: (1)求出每一个样本属于哪个分布 (2)求出每一个分布对应的参数

2、举例说明
身高问题使用EM算法求解步骤:
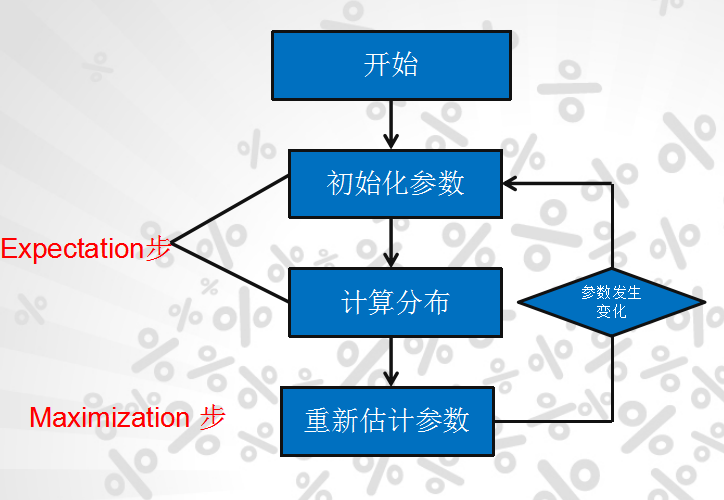
(1)初始化参数:先初始化男生身高的正态分布的参数:如均值=1.7,方差=0.1
(2)计算每一个人更可能属于男生分布或者女生分布;
(3)通过分为男生的n个人来重新估计男生身高分布的参数(最大似然估计),女生分布也按照相同的方式估计出来,更新分布。
(4)这时候两个分布的概率也变了,然后重复步骤(1)至(3),直到参数不发生变化为止。
3、算法推导
已知:样本集X={x(1),…,x(m))},包含m个独立的样本;
未知:每个样本i对应的类别z(i)是未知的(相当于聚类);
输出:我们需要估计概率模型p(x,z)的参数θ;
目标:找到适合的θ和z让L(θ)最大。
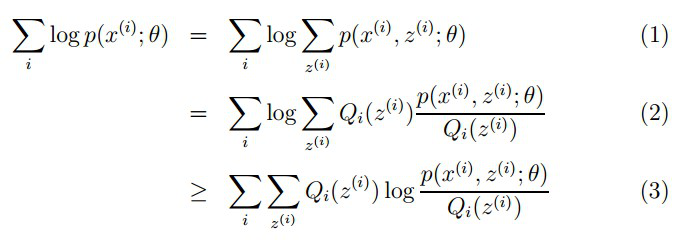
要使L(θ)最大,我们可以不断最大化下界J,来使得L(θ)不断提高,达到最大值。
问题:
什么时候下界J(z,Q)与L(θ)在此点θ处相等?
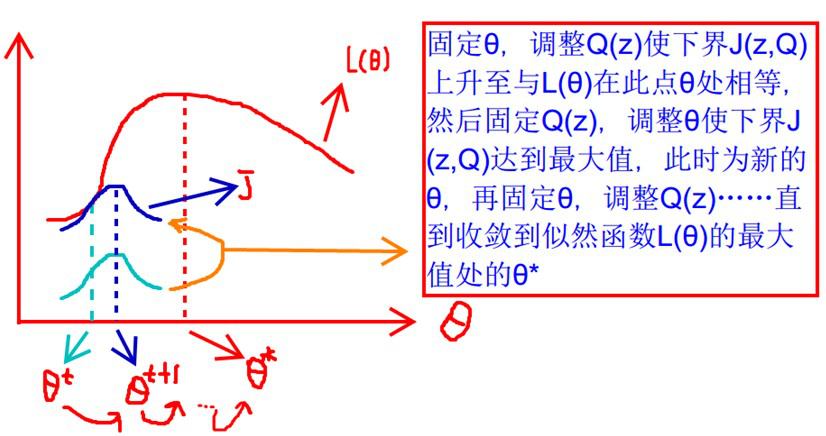
根据Jensen不等式,自变量X是常数,等式成立。即: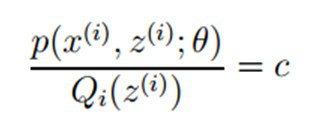
由于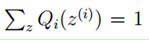 ,则可以得到:分子的和等于c
,则可以得到:分子的和等于c
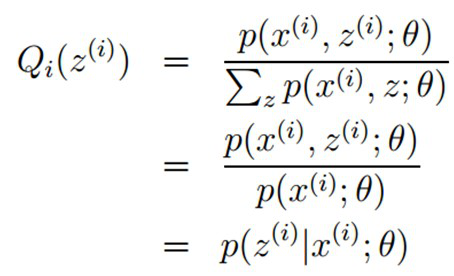
在固定参数θ后,使下界拉升的Q(z)的计算公式,解决了Q(z)如何选择的问题。这一步就是E步,建立L(θ)的下界。接下来的M步,就是在给定Q(z)后,调整θ,去极大化L(θ)的下界J。
4、算法流程
1)初始化分布参数θ; 重复以下步骤直到收敛:
E步骤:根据参数初始值或上一次迭代的模型参数来计算出隐性变量的后验概率,其实就是隐性变量的期望。作为隐藏变量的现估计值:

M步骤:将似然函数最大化以获得新的参数值:
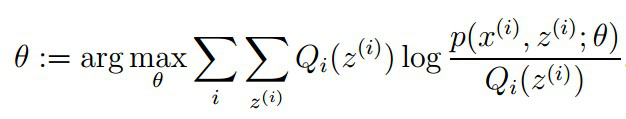
5、总结
期望最大算法(EM算法)是一种从不完全数据或有数据丢失的数据集(存在隐含变量)中求解概率模型参数的最大似然估计方法。
三、EM算法的初始化研究
1、问题描述
EM算法缺陷之一:传统的EM算法对初始值敏感,聚类结果随不同的初始值而波动较大。总的来说,EM算法收敛的优劣很大程度上取决于其初始参数。
我看了一篇论文:地址:https://yunpan.cn/cqmW9vurLFmDT 访问密码 0e74
本篇论文采用的方法:采用一种基于网格的聚类算法来初始化EM算法。
2、基本思想
基于网格的聚类算法将数据空间的每一维平均分割成等长的区间段, 从而将数据空间分成不相交的网格单元。由于同个网格单元中的点属于同一类的可能性比较大, 所以落入同一网格单元中的点可被看作一个对象进行处理, 以后所有的聚类操作都在网格单元上进行。 因此,基于网格的聚类过程只与网格单元的个数有关, 聚类的效率得到了很大的提高。
3、算法步骤
(1)定义:

(2)相似度:数据对象间的相似性是基于对象间的距离来计算的。
(3)输入输出:

(4)算法步骤


4、总结
我觉得这篇论文的主要思想应该是这样的:就拿身高举例。它就是首先做一个预处理,将身高在一个范围内(例如1.71至1.74)的分成一个网格,再看这个网格占全部数据的多少,以此判断出该网格为高密度还是低密度,然后循环算出所有网格的,再使用EM算法计算哪些高密度网格,这样会使整个算法收敛的快一些。还有一些其他的论文也是讲的这个。
转自:http://blog.51cto.com/9269309/1892833
摘要
EM算法主要分为两个步骤:E-step和M-step,主要应用在概率模型中。机器学习中,概率模型在进行参数估计时,我们主要应用的是最大似然估计,所以在对EM算法进行讨论时,是离不开最大似然估计的。EM算法主要是用来解决那些样本中存在隐变量的情况。E-step固定模型参数通过数学模型求解隐变量,M-step根据E-step求得的隐变量在通过最大似然估计最大化似然函数从而求出模型的参数,这样相互的迭代,从而得到模型的局部最优解。EM算法主要应用在聚类算法中,因为一般情况下聚类问题都存在一个隐变量。
什么是隐变量
样本中存在隐变量即我们在对数据进行采样中,可以认为隐变量是那些我们不能通过数据采样所能确定的属性。如果不存在隐变量,那对于一些聚类模型,我们的参数求解就简单很多,比如k-means,k-means只是利用了EM算法的思想。我们有一批数据,想利用k-means算法来进行聚类分析,对于k-means算法,我们要确定的是k和k个质心,假如我们在对这批数据采样时已经知道他们分为4类,而且采样前就已经把数据给分好类了,已经知道了,还用聚类算法干嘛,我们这是暂时的假设用他来举例说明什么是隐变量,那么我们在用k-means算法时就变得很简单了,直接求出这k个质心,而不用我们所熟知的k-means算法的计算步骤。之所以我们使用我们所熟知的k-means算法的步骤,那是因为我们不知道每个样本应该归属于哪个类以及他们存在多少个聚类中心比较合适。那么这个隐变量就是每一个样本应该归属于哪个类。在举一个例子,高斯混合模型,这个是典型用到了EM算法的思想,如果对这个模型不太清楚,可以网上查资料。同样,我们也有这样一批数据,在采样中,我们就已经知道k和每个样本应该属于哪个类,那么我们所要做的工作就是把每一类数据拿出来,直接通过均值和方差就可以求出每一个高斯函数的模型了,而不需要再进行EM算法通过最大似然估计来计算我们的高斯混合模型参数了。而现实的应用中是我们不知道这样的一批数据应该分为几个类以及每一个样本应该属于哪一个类,那么这就是隐变量。这样的问题和先有鸡还是先有蛋的问题差不多,当我们知道数学模型的参数后,我们就知道了样本应该属于哪个类,同时当我们知道隐变量后,我们也就知道样本属于哪个类,从而得到数学模型的参数,但是不幸的是在开始的时候我们只有样本,隐变量和模型参数都不知道。
凸函数和凹函数以及其性质
为什么要讲这个,因为EM算法得以实施的基础就是函数的凹凸性以及凹凸函数的一些性质。所以这里还是说一下吧。
在高等数学和数学分析(数学专业的书)对于凹凸函数的定义可能有些不一样。这个没有关系只是叫法不同,但是他们这些图形和图形的性质是一样的。
凸函数定义:函数的二阶导函数在一定的区间内大于等于零,性质如下
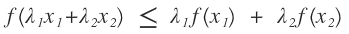
如下图:
凹函数的定义:函数的二阶导函数在一定的区间内小于等于零,性质如下:
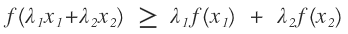
如下图所示:
最大似然估计步骤
因为在概率模型中,进行参数估计一般都采用最大似然估计
1、确定概率模型求出似然函数
2、对似然函数取log,把连乘变为求和
3、对变换后的似然函数求导,并另导数等于0,然后整理得到似然方程组
4、求解似然方程组,得到模型参数
EM算法
假设我们有一批数据样本{x(1),…,x(n)},,样本容量为n,概率模型为p(x,z)来对我们的数据进行拟合。根据概率模型的参数估计算法,我们可以得到似然函数:
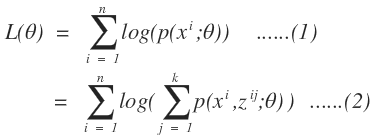
上式中(1)我们是通过最大似然估计的步骤获取的,从(1)到(2)引入了样本属于某一个类的概率函数,从而对某一个样本求得该样本属于某个类的全概率公式,即引入了隐变量z。
当我们采用传统的概率模型求解参数的方法即最大似然估计,对上述式子进行求导数,从而得到似然方程:
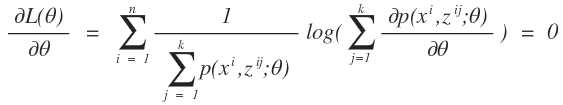
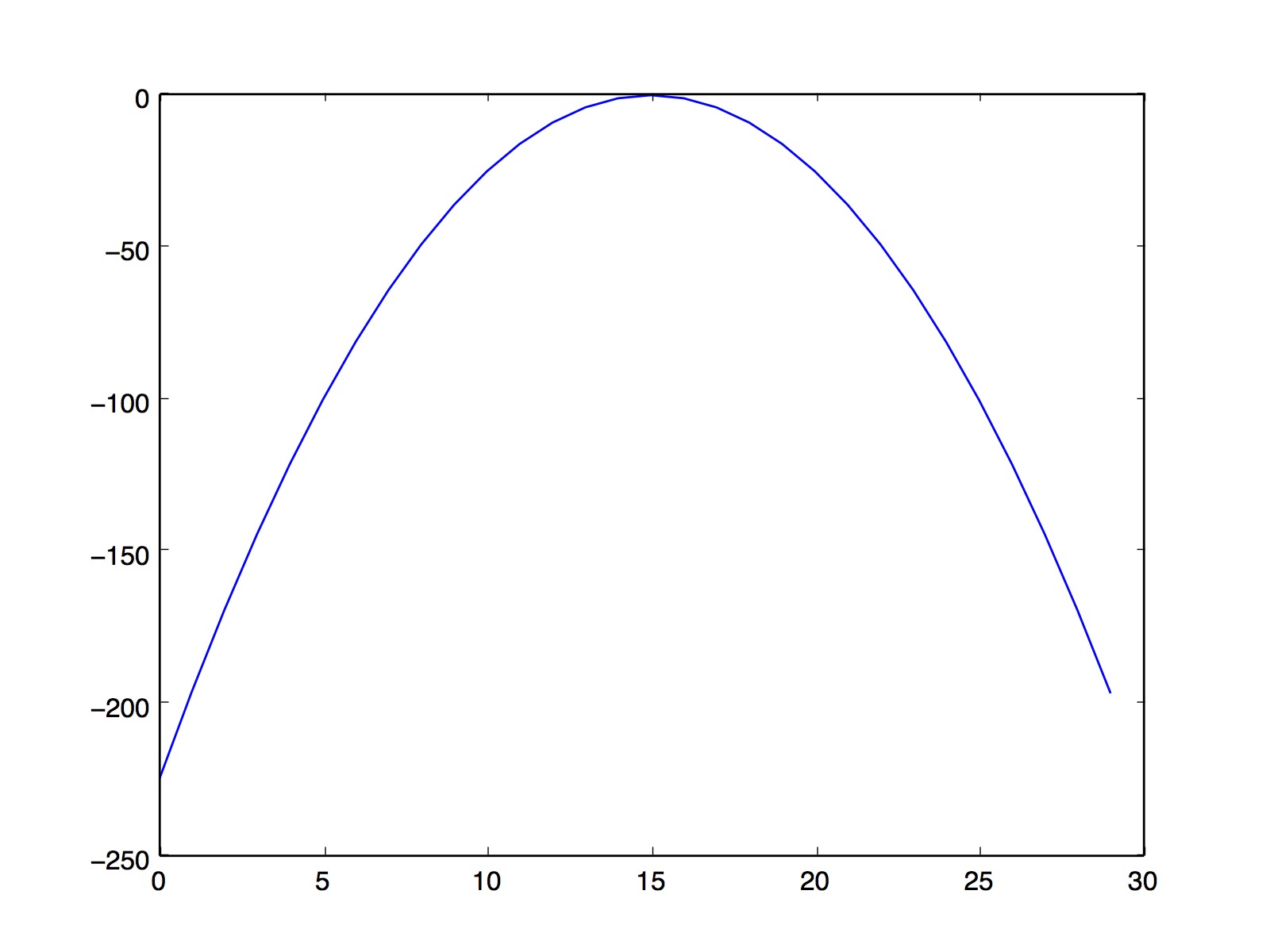
我们会发现上述似然方程中存在对数,并且对数里面是个求和公式,这种求解是很难得到参数的解析解的。遇到胡同了,我们就要想一下拐一下弯,既然这个公式无法求解的难点在于对数里面有求和公式,那么我们能不能采用什么办法把对数后面的求和号给拿到外面。再看看对数函数的性质是什么样子的?对数函数是一个凹函数那么他肯定满足凹函数的基本性质:
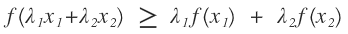
把上式进行变换:
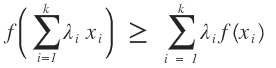
我们的目标函数和凹函数的性质还差那么一点点的差距,那么我们就认为对于每一个实例i,用Qi表示对应于隐含变量即其属于哪个类的概率分布,我们这是对于一个样本而言的,那么样本有n个,就会存在n个这样的Qi的函数分布,一定要把这一点弄明白。这个Qi表示的样本i对应于k个类,其属于这k个类的概率分布。那么Qi应该满足的条件是:
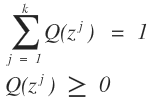
那么我们就可以把我们的似然函数进行改写了:
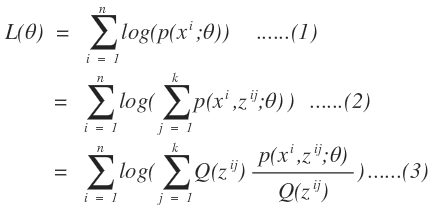
这样一看就和我们的凹函数性质一致了吧。于是我们可以把上述函数通过凹函数的性质进行变换:
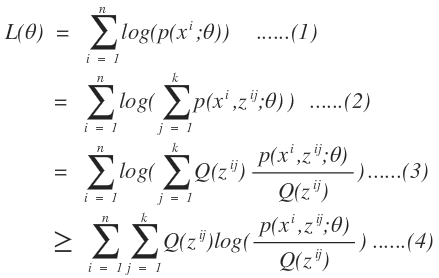
既然原函数无法得到最优解,我们可以通过调整原函数的下界函数,对原函数的下界函数求最大值,从而使原函数逐步逼近最优解或者得到一个局部最优解。即我们不停的求解上式中(4)的最大值,从而是我们原函数逼近最优解。
看到这可能会有一个问题,通过最大似然估计得到的原似然方程无法得到解析解,为什么变成(4)就可以得到了呢?我们在已知隐变量的前提下对模型参数进行求偏导得到的似然方程中,发现log已经不复存,已经变成了我们熟悉的线性方程组或者非线性方程组(这个跟数学模型有关),一般情况下这个就可以利用线性代数的理论进行求解了啊。
因此EM算法的基本思想就是通过引入隐变量,先得到样本属于某一个类的概率,然后再使用最大似然估计最大化似然函数来求解参数,得到参数以后,数学模型就已经确定,那么我就可以得到样本属于哪个类了,从而得到隐变量的值,因此就用迭代的进行求解最终得到问题的解。当我们引入隐变量后,整个似然函数就会存在两类参数类型:隐变量和数学模型的参数。那么EM算法采用的步骤如下:
E-step: 通过固定数学模型的参数,利用现有样本对隐变量进行参数估计,即求出隐变量的期望也就是我们期望样本属于哪一个类
M-step: 通过E-step求得的隐变量,对数学模型参数求导,最大化似然函数。
隐变量的求解
对于EM算法,我们是不断的逼近最优值,那么E-step计算的是什么呢?因为在凹函数的性质中上述不等式取等号的前提条件是xi为常数
则:
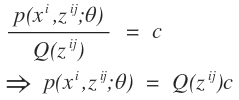
对上式进行求和:
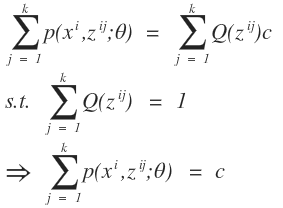
通过上述两个式子我们进行变换得到:
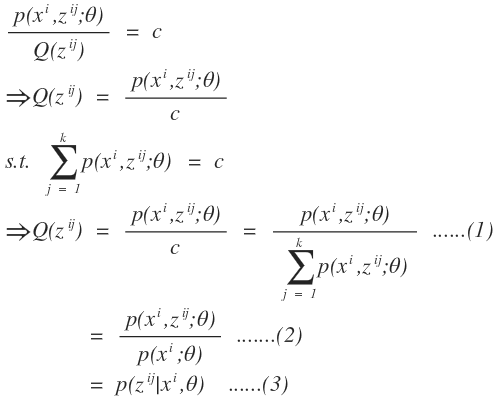
在上式中从(1)到(2)为什么会是这样,我们按照举个例子,用二元一次函数的积分问题来看待这个问题的推导,因为积分的实质也是一种求和对函数下部的面积进行无线的拆分然后再求和。如下式的二元函数:
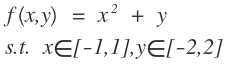
然后我们对上面的二元一次函数对y进行求积分:
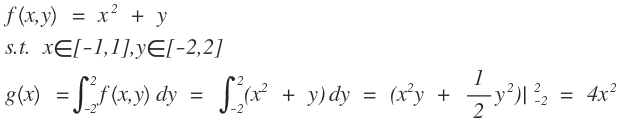
从而消除了变量y,同样的道理,从(1)到(2)的过程中,我们分母对样本i的所有的可能隐变量取值求和,从而把隐变量z给消除,从而得到公式(2)从(2)到(3)是通过条件概率的公式得到的。因此我们可以发现隐变量其实就是在固定数学模型参数和已知数据样本的情况下的后验概率。
以上只是理论部分,下面我们简单说一下EM算法的实际应用。
在实际应用中我们不会按照上面公式来推导我们的算法。我们只知道两个点就可以了:隐变量的求解和已知隐变量的前提下最大化似然函数从而来求解数学模型的参数。
隐变量的求解:我们已经知道其是样本和数学模型参数的后验概率,那么我就可以根据实际的情况来推导计算这个后验概率从而得到我们的隐变量和参数的关系表达式从而用于迭代求解即为E-step
最大化似然函数:这个是我们最大似然估计算法的步骤了即M-step。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号