欧拉降幂公式

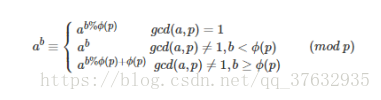
在进行超高次幂取模运算时，通过欧拉降幂公式结合快速幂快速乘可以很好的减少运算

例题

直接套公式即可加上快速幂即可

#include <cstdio>
#include <iostream>
#include <cmath>
#define endl "\n"
using namespace std;
typedef long long ll;
ll euler_phi(ll n){
	ll m = ll(sqrt(n + 0.5));
	ll ans = n;
	for (ll i = 2; i <= m; i++){
		if(n % i == 0){
			ans = ans / i * (i - 1);
			while (n % i == 0) n /= i;
		}
	}
	if(n > 1)ans = ans / n * (n - 1);
	return ans;
}
ll qc(ll x,ll y,ll mod)
{
    return (x*y-(ll)((long double)x/mod*y)*mod+mod)%mod;     
}
ll qpow(ll x, ll y, ll m){
	ll res = 1;
	res %= m;
	while (y){
		if(y & 1){
			res = qc(res, x, m);
		}
		y >>= 1;
		x = qc(x, x, m);
	}
	return res % m;
}
int main()
{
#ifdef endl
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);
#endif
	ll a, b, c, mod, k;
	string B; 
	while (cin >> a >> B >> c){
		int len = B.length();
		b = 0;
		k = 1;
		mod = euler_phi(c);
		for (int i = len - 1; i >= 0; i--){
			b += (B[i] - '0') * k;
			b %= mod;
			k *= 10;
			k %= mod;
		}
		ll res = qpow(a, b % mod + mod, c);
		cout << res << endl;
	}
	return 0;
}