一、树

1.基本概念

  • 用来模拟具有树状结构性质的数据集合。
  • 连接的节点具有父子关系，和图相比树能表示节点间的层次关系。

2、名词解释

  • 节点的度：一个节点子树的个数
  • 树的度：一个树中，所有节点的度的最大值就成为树的度
  • 根节点：树的第一层的节点，也是没有双亲的节点

  • 高度/深度：从根开始到最多层次，最底下的节点，其长度就成为树的高度，根的高度为1

3、二叉树

  • 其每一个节点的度都<=2。
  • 在二叉树第i层最多有2^(i-1)个节点。
  • 深度为k的二叉树最多有2^k-1个节点。
  • 对于任何一棵二叉树T,叶子节点数为n0,度为2的节点数为n2则n0=n2 + 1。

二叉树的特殊类型有：满二叉树、完全二叉树、二叉查找树、平衡二叉查找树（AVL树）、红黑树

3.1 满二叉树

除了最后一层，其它层的结点都有两个子结点。

  • 在二叉树第i层有2^(i-1)个节点。
  • 深度为k的二叉树有2^k-1个节点。

3.2 完全二叉树

除了最后一层结点，其它层的结点数都达到了最大值；同时最后一层的结点都是按照从左到右依次排布。

  • 具有n个节点的完全二叉树的深度为[log2n] + 1,
  • 如果对一棵有n个节点的完全二叉树(深度为[log2n] + 1)的节点按层序编号，对任一节点i(1<=i<=n)有:
  • 如果i=1,则i是根节点,无双亲;否则其双亲是 i/2.
  • 如果2i>n,则节点i无左孩子(节点i为叶节点);否则左孩子为2i.
  • 如果2i+1>n,则节点i无右孩子(节点i为叶子节点);否则右孩子为2i+1.

3.3 二叉查找树

是一棵空树，或者：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别为二叉排序树。

3.4 平衡二叉查找树（AVL树）

  • 它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
  • 平衡二叉树的产生是为了解决二叉排序树在插入时发生线性排列，退化成链表的现象。
  • 平衡二叉树（AVL）为了追求高度平衡，所付出的代价就是当对树中结点进行插入和删除时，需要经过多次旋转实现复衡。这导致AVL的插入和删除效率并不高。

四种旋转方式：

（1）LR型：左叶子结点插入右子节点

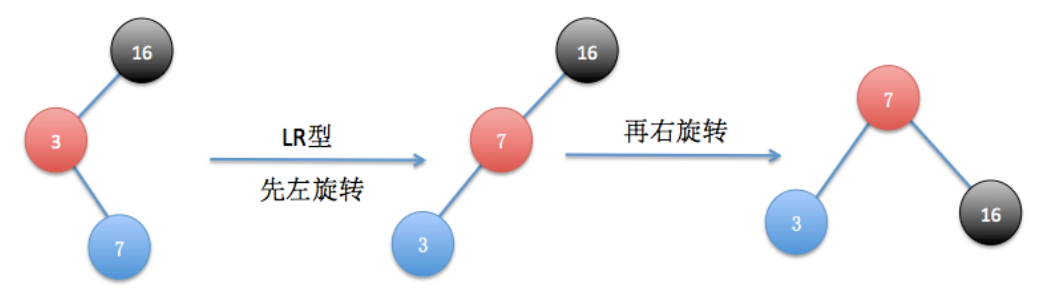
 先通过以3为旋转中心，进行左旋转，结果如图所示，然后再以7为旋转中心进行右旋转，旋转后恢复平衡了。

（2）LL型：左叶子结点插入左子节点

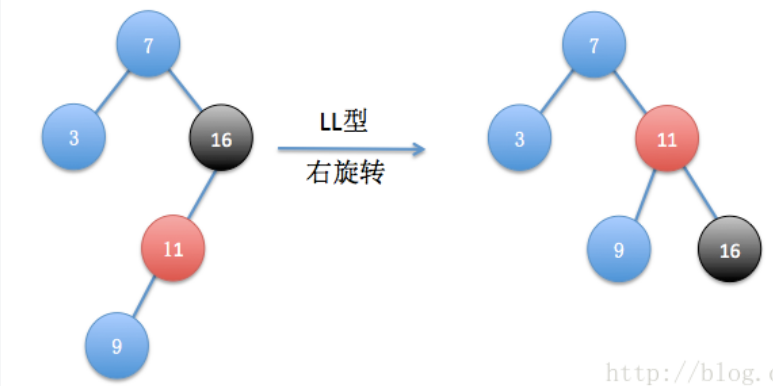
 只用经过一次右旋转

 （3）RR型：右叶子结点插入右子节点

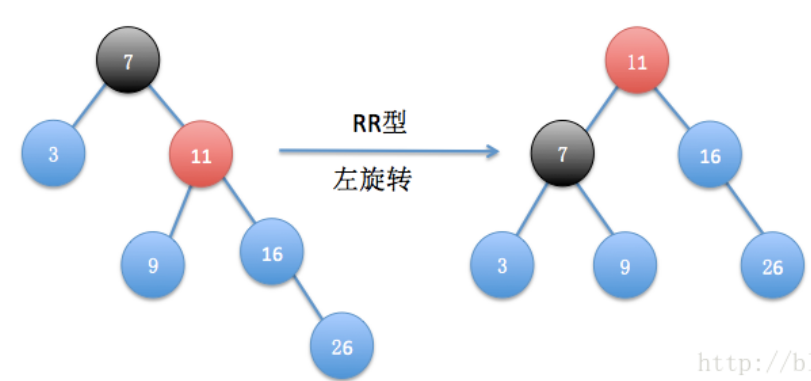
对插入节点的父节点进行左旋转

（4）RL型：

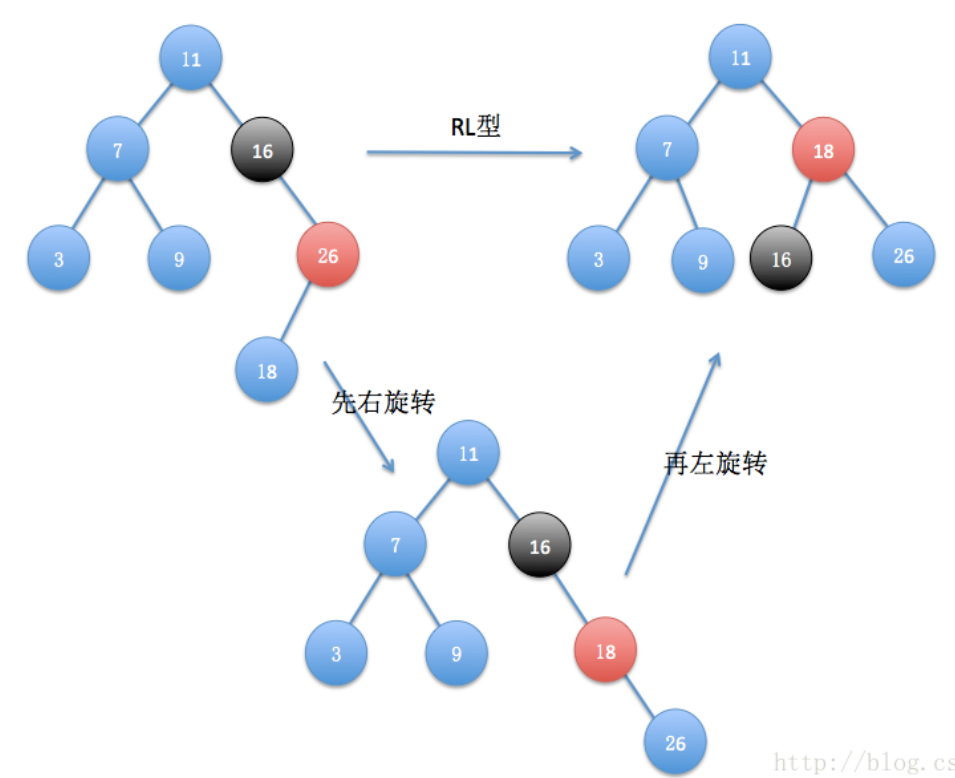
 对插入节点先右旋转再左旋转

3.5 红黑树

红黑树是一种自平衡的二叉搜索树，它保证了每个节点都有一个颜色属性，可以是红色或者黑色，并且满足以下五个性质：

  1. 根节点是黑色的。
  2. 每个叶子节点（NULL节点）是黑色的。
  3. 如果一个节点是红色的，则其子节点必须是黑色的。
  4. 对于每个节点，从该节点到其所有后代叶子节点的简单路径上，均包含相同数目的黑色节点。
  5. 空节点被视为黑色。

这些性质确保了红黑树具有较好的平衡性和搜索效率，在插入、删除等操作时能够保持树的平衡，使得最坏情况下的时间复杂度为 O(log n)。

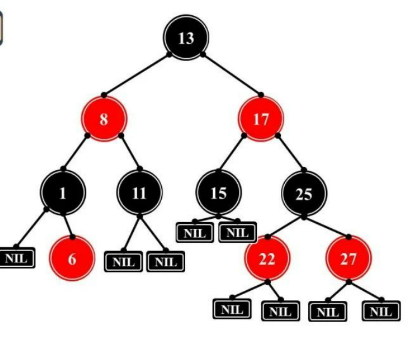
与AVL树的区别：

1、红黑树的插入和删除操作效率比AVL树高，因为红黑树在插入和删除节点时只需进行 O(1) 次数的旋转和变色操作，即可保持基本平衡状态，而不需要像 AVL 树一样进行 O(logn) 次数的旋转操作。

2、红黑树并不追求严格的平衡，而是大致的平衡。正因如此，红黑树的查询效率稍有下降，因为红黑树的平衡性相对较弱，可能会导致树的高度较高，

3、多叉树

B树和B+树都是一种多叉平衡搜索树

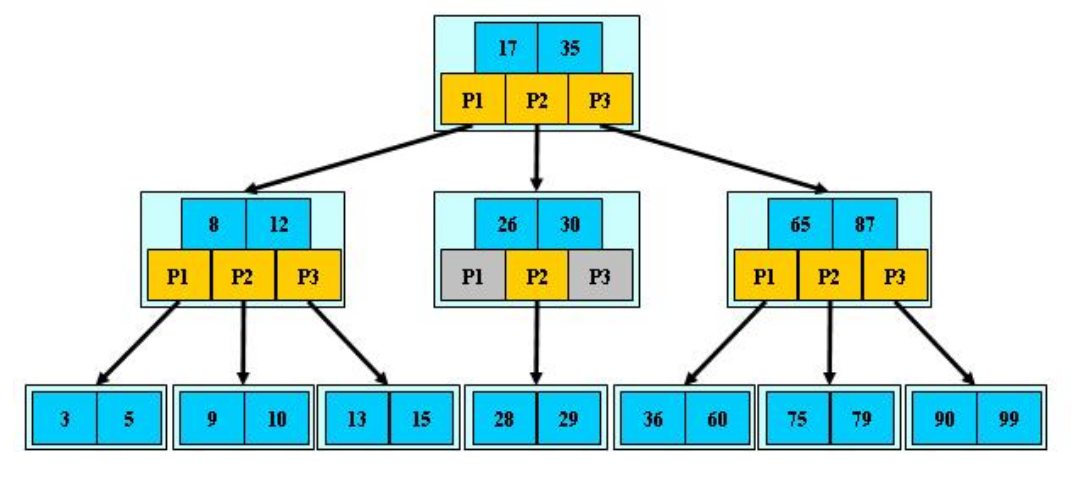
3.1B树

B树的定义如下，假设有M个子节点：

 　　1.定义任意非叶子结点最多只有M个儿子；且M>2；

       2.根结点的儿子数为[2, M]；

       3.除根结点以外的非叶子结点的儿子数为[M/2, M]；

       4.每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）

       5.非叶子结点的关键字个数=指向儿子的指针个数-1；

       6.非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；

       7.非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字大于K[i-1],小于 K[i]的子树；

       8.所有叶子结点位于同一层；

 

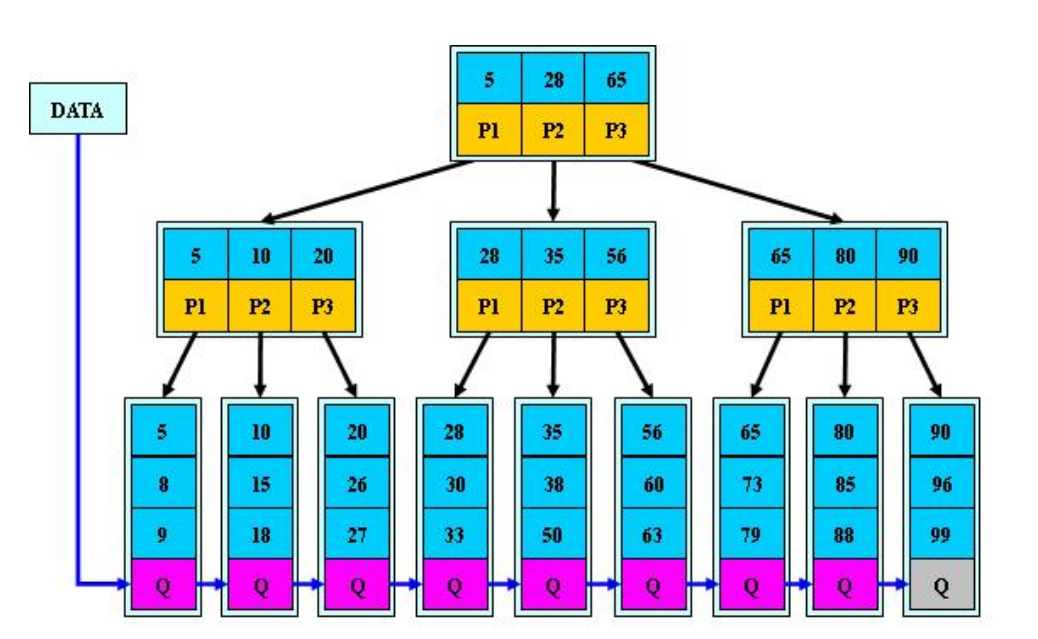
3.2 B+树

其定义基本与B树同，除了：

       1.非叶子结点的子树指针与关键字个数相同；

       2.非叶子结点的子树指针P[i]，指向关键字值大于等于K[i]小于K[i+1] （左闭右开）的子树

       5.为所有叶子结点增加一个链指针；

       6.所有关键字都在叶子结点出现；

 

区别：

  B树 B+树
存储结构 每个节点既存储数据，也存储子节点指针 非叶子节点只存储子节点指针，数据只存储在叶子节点中，

b+树的中间节点不保存数据，所以磁盘页能容纳更多节点元素，更“矮胖”
叶子节点 叶子节点可以包含数据，也可以不包含数据 叶子节点必须包含全部数据，且按照键值大小排序形成一个链表。
遍历方式 为了遍历全部数据，需要对每个节点进行遍历 B+树可以通过遍历叶子节点的链表来获取所有数据
范围查询 范围查询需要对每个节点进行遍历，相对较慢 通过遍历叶子节点的链表来快速定位并返回符合条件的数据
关键字个数 非叶子结点的关键字个数=指向儿子的指针个数-1 非叶子结点的子树指针与关键字个数相同
子节点指针的范围 开区间，P[i]指向关键字大于K[i-1],小于 K[i]的节点 左闭右开，P[i]指向关键字值大于等于K[i]小于K[i+1] （左闭右开）的节点

 

二、堆

  • 堆在物理层面上，表现为一组连续的数组区间；将整个数组看作是堆。

    堆在逻辑结构上，一般被视为是一颗完全二叉树。

  • 对于任意一个父节点的序号n来说（这里n从0算），它的子节点的序号一定是2n+1，2n+2，因此可以直接用数组来表示一个堆。
  • 堆中某个节点的值总是不大于或不小于其父节点的值。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

由于堆的根节点是序列中最大或者最小值，因而可以在建堆以及重建堆的过程中，筛选出数据序列中的极值，从而达到排序或者挑选topK值的目的。

1、创建堆，向下调整：

public class HeapTest {
    /**
     * 小堆的向下调整，要求满足向下调整的前提
     * @param array 堆所在的数组
     * @param size  前 size 个元素视为堆中的元素
     * @param index 要调整位置的下标
     */
    public static void shiftDown(long[] array, int size, int index) {
        // 只要看到 int 类型的，基本就是下标或者个数，不是元素
 
        // 这里直接 while(true)即可
        // while (2 * index + 1 < size) {    如果这么写，下面就不用再进行叶子的判断
        while (true) {
            // 1. 判断 index 所在位置是不是叶子
            // 逻辑上，没有左孩子一定就是叶子了（因为完全二叉树这个前提）
            int left = 2 * index + 1;
            if (left >= size) {
                // 越界 -> 没有左孩子 -> 是叶子 -> 调整结束
                return; // 循环的出口一：走到的叶子的位置
            }
 
            // 2. 找到两个孩子中的最值【最小值 via 小堆】
            // 先判断有没有右孩子
            int right = left + 1;       // right = 2 * index + 2
            int min = left;             // 假设最小值就是左孩子，所以 min 保存的最小值孩子所在的下标
            if (right < size && array[right] < array[left]) {
                // right < size 必须在 array[right] < array[left] 之前，不能交换顺序
                // 因为先得确定有右孩子，才有比较左右孩子的意义
                // 有右孩子为前提的情况下，然后右孩子的值 < 左孩子的值
                min = right;            // min 应该是右孩子所在的下标
            }
 
            // 3. 将最值和当前要调整的位置进行比较，判断是否满足堆的性质
            if (array[index] <= array[min]) {
                // 当前要调整的结点的值 <= 最小的孩子值；说明这里也满足堆的性质了，所以，调整结束
                return; // 循环的出口一：循环期间，已经满足堆的性质了
            }
 
            // 4. 交换两个值，物理上对应的就是数组的元素交换 min 下标的值、index 下标的值
            long t = array[index];
            array[index] = array[min];
            array[min] = t;
 
            // 5. 再对 min 位置重新进行同样的操作（对 min 位置进行向下调整操作）
            index = min;
        }
    }
 
    public static void main(String[] args) {
        long[] array = { 27, 15, 19, 18, 28, 34, 65, 49, 25, 37 };
        shiftDown(array,9,0);
    }
}

2、堆的插入

堆的插入总共需要两个步骤：

1️⃣. 先将元素放入到最后

2️⃣. 将最后新插入的节点向上调整，直到满足堆的性质 ；

 1 // 注意：上图是按照大堆来调整的，注意比较方式
 2 public void shiftUp(int child) {
 3     // 找到child的双亲
 4      int parent = (child - 1) / 2;
 5     
 6     while (child > 0) {
 7         // 如果双亲比孩子大，parent满足堆的性质，调整结束
 8         if (array[parent] > array[child]) {
 9             break;
10        }
11         else{
12             // 将双亲与孩子节点进行交换
13             int t = array[parent];
14             array[parent] = array[child];
15             array[child] = t;
16         
17             // 小的元素向下移动，可能到值子树不满足对的性质，因此需要继续向上调增
18             child = parent;
19             parent = (child - 1) / 1;
20        }
21    }
22 }
View Code

3. 堆的删除(poll)

具体如下：（ 注意：堆的删除一定删除的是堆顶元素。） 

1️⃣. 将堆顶元素对堆中最后一个元素交换；

2️⃣. 将堆中有效数据个数减少一个；

3️⃣. 对堆顶元素进行向下调整；

 1    public long poll() {
 2         // 返回并删除堆顶元素
 3         if (size < 0) {
 4             throw new RuntimeException("队列是空的");
 5         }
 6  
 7         long e = array[0];
 8  
 9         // 用最后一个位置替代堆顶元素，删除最后一个位置
10         array[0] = array[size - 1];
11         array[size - 1] = 0;        // 0 代表这个位置被删除了，不是必须要写的
12         size--;
13  
14         // 针对堆顶位置，做向下调整
15         shiftDown(array, size, 0);
16  
17         return e;
18     }
View Code

 三、散列表

散列表也叫哈希表，是一种通过键值对直接访问数据的数据结构。散列表通过哈希映射，将key映射到对应的地址。

哈希冲突处理方式有很多，常用的包括以下几种：

开放地址法（也叫开放寻址法）：这时对计算出来的地址进行一个探测再哈希，比如往后移动一个地址，如果没人占用，就用这个地址。

再哈希法：在产生冲突之后，使用关键字的其他部分继续计算地址，如果还是有冲突，则继续使用其他部分再计算地址。这种方式的缺点是时间增加了。

链地址法：链地址法其实就是对Key通过哈希之后落在同一个地址上的值，做一个链表。其实在很多高级语言的实现当中，也是使用这种方式处理冲突的。

公共溢出区：这种方式是建立一个公共溢出区，当地址存在冲突时，把新的地址放在公共溢出区里。

目前比较常用的冲突解决方法是链地址法，一般可以通过数组和链表的结合达到冲突数据缓存的目的。

 

四、图

 

图结构一般包括顶点和边。

1、图的分类

根据边的方向性，还可将图分为有向图和无向图。

如果任意两个顶点之间都存在边叫完全图：

完全无向图：若有n个顶点的无向图有n(n-1)/2 条边, 则此图为完全无向图。

完全有向图：有n个顶点的有向图有n(n-1)条边, 则此图为完全有向图。

如果对于图中任意两个顶点都是连通的，则成G是连通图：

极大联通子图：加入任何一个节点，子图将不再联通

最小联通子图：删除任何一条边，子图将不再联通

有向的连通图称为强连通图。

2、图的存储

1、邻接矩阵

邻接矩阵用两个数组保存数据。一个一维数组存储图中顶点信息，一个二维数组存储图中边或弧的信息。

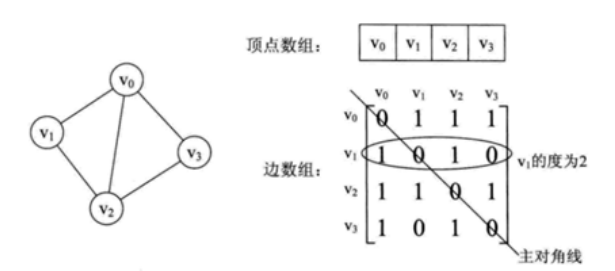
无向图中二维数组是个对称矩阵。

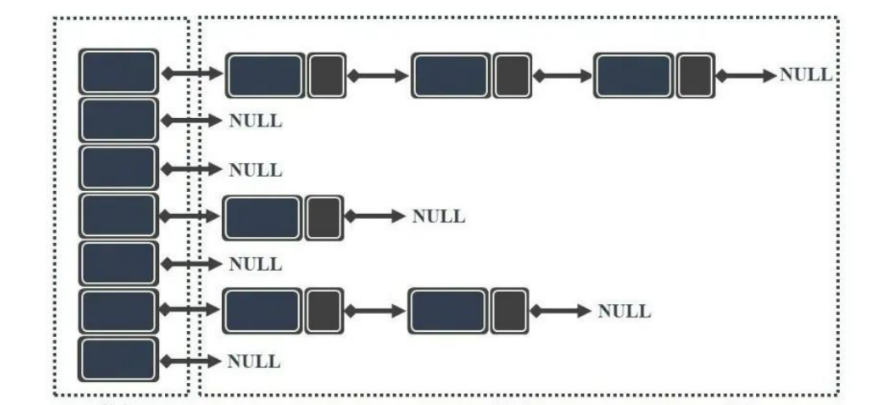
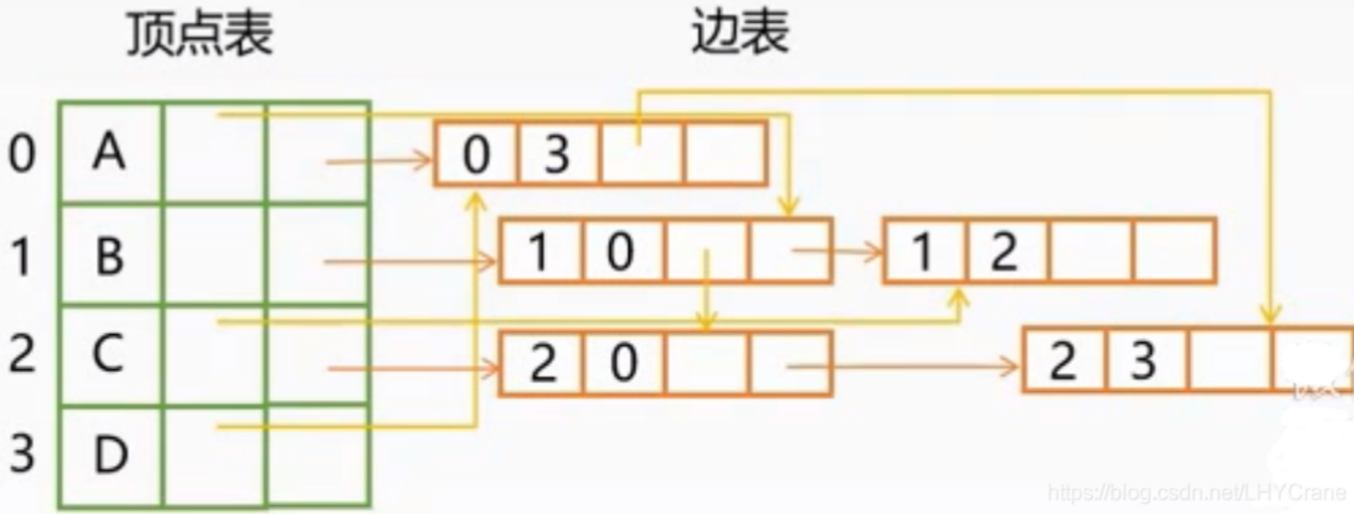
2、邻接表

邻接表：数组和链表相结合的存储方法为邻接表。

  • 图中顶点用一个一维数组存储。

  • 图中每个顶点Vi的所有邻接点构成一个线性表。

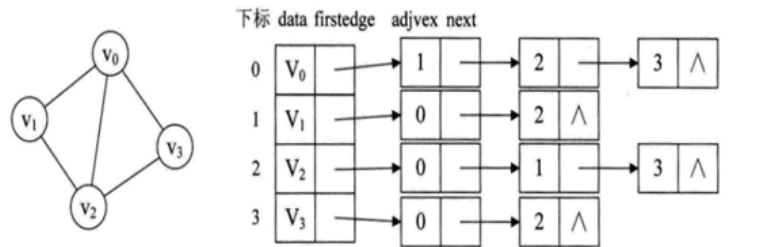
 有向图也可以用邻接表，出度表叫邻接表，入度表尾逆邻接表。

3、十字链表

将有向图的邻接表和逆邻接表结合起来得到的。

1、重新定义表头结构

        只需对表头结构稍加改动，增加firstIn和firstOut两个指针域，分别指向以A为弧尾和以A为弧头的第一个顶点地址。

2、重新定义节点结构

边表每个结点结构如下：

tailvex：弧起点的下标 headvex：弧终点的下标 headlink:入边指针 taillink:出边指针

 

3、图的遍历

DFS:深度优先遍历，一般用堆或栈来辅助实现DFS算法。其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，如果遇到死路就往回溯，回溯过程中如果遇到没探索过的支路，就进入该支路继续深入。

搜索图所有节点的DFS代码如下：

 1 import java.util.*;
 2 
 3 public class Graph {
 4     private int V; // 图中节点数
 5     private LinkedList<Integer> adj[]; // 邻接表表示图
 6 
 7     public Graph(int v) {
 8         V = v;
 9         adj = new LinkedList[v];
10         for (int i = 0; i < v; ++i)
11             adj[i] = new LinkedList();
12     }
13 
14     public void addEdge(int v, int w) {
15         adj[v].add(w);
16     }
17     
18     public void DFS(int s) {
19         boolean visited[] = new boolean[V];
20         Stack<Integer> stack = new Stack<Integer>();
21 
22         visited[s] = true;
23         stack.push(s);
24 
25         while (!stack.isEmpty()) {
26             s = stack.pop();
27             System.out.print(s + " ");
28 
29             Iterator<Integer> i = adj[s].listIterator();
30             while (i.hasNext()) {
31                 int n = i.next();
32                 if (!visited[n]) {
33                     visited[n] = true;
34                     stack.push(n);
35                 }
36             }
37         }
38     }
39 
40     public static void main(String args[]) {
41         Graph g = new Graph(4);
42 
43         g.addEdge(0, 1);
44         g.addEdge(0, 2);
45         g.addEdge(1, 2);
46         g.addEdge(2, 0);
47         g.addEdge(2, 3);
48         g.addEdge(3, 3);
49 
50         System.out.println("Depth First Traversal (starting from vertex 2)");
51         g.DFS(2);
52     }
53 }

 

深度优先搜索应用：先序遍历，中序遍历，后序遍历

BFS:广度优先遍历，BFS是从根节点开始，沿着树(图)的宽度遍历树(图)的节点。如果所有节点均被访问，则算法中止。一般用队列数据结构来辅助实现。

广度优先搜索应用：层序遍历、最短路径、求二叉树的最大高度

 1 import java.util.*;
 2 
 3 public class Graph {
 4     private int V; // 图中节点数
 5     private LinkedList<Integer> adj[]; // 邻接表表示图
 6 
 7     public Graph(int v) {
 8         V = v;
 9         adj = new LinkedList[v];
10         for (int i = 0; i < v; ++i)
11             adj[i] = new LinkedList();
12     }
13 
14     public void addEdge(int v, int w) {
15         adj[v].add(w);
16     }
17     
18     public void BFS(int s) {
19         boolean visited[] = new boolean[V];
20         LinkedList<Integer> queue = new LinkedList<Integer>();
21 
22         visited[s] = true;
23         queue.add(s);
24 
25         while (queue.size() != 0) {
26             s = queue.poll();
27             System.out.print(s + " ");
28 
29             Iterator<Integer> i = adj[s].listIterator();
30             while (i.hasNext()) {
31                 int n = i.next();
32                 if (!visited[n]) {
33                     visited[n] = true;
34                     queue.add(n);
35                 }
36             }
37         }
38     }
39 
40     public static void main(String args[]) {
41         Graph g = new Graph(4);
42 
43         g.addEdge(0, 1);
44         g.addEdge(0, 2);
45         g.addEdge(1, 2);
46         g.addEdge(2, 0);
47         g.addEdge(2, 3);
48         g.addEdge(3, 3);
49 
50         System.out.println("Breadth First Traversal (starting from vertex 2)");
51         g.BFS(2);
52     }
53 }