2025 ICPC Nanchang Invitational and Jiangxi Provincial Collegiate Programming Contest
2025 ICPC Nanchang Invitational and Jiangxi Provincial Collegiate Programming Contest/南昌邀请赛
赛前准备
本来打算是去西安的,因为西安打到牌子就发ic区域赛的名额,但是由于西安偷跑而且当时我是唯一一天补交的,所以没抢到票,然后武汉也没抢到,因为他优先队列,那么只能抢南昌了,还好南昌有保底名额,基本上每个学校都发了一个。
ps:(当时因为没抢到名额绝望的一夜,但好在最后还是抢到了南昌)
然后说下我们的队伍配置,我一个青名(接近蓝名),但应该是有蓝名水平的吧?然后我一个队友是为了让他a报名费来的蓝桥省二,另外一个是留学的来挂名的雅思留学副歌。好吧简单来说就是单挑。
赛前一天
面基了好多好多的群u,甚至拿到了羊神的笔记本和签名,还有sserxhs的签名
这里有个小插曲,我们一堆人在报道的地方蹲羊神,但是羊神躲在小角落里发消息,结果没想到他就躲我们后面的视野盲区里,最后被发现还是被我们团团包围了hhh
(下是小羊肖恩,左是hsn,又是醋酸锌,上是我)

上我,左hsn,右良_穗遇而安,下洛依

1-醋,2-鱼,3-hsn,4-sserxhs,5-良_穗遇而安,6-小羊

这一桌就不一一介绍了

在校园内的随便拍拍






题解
Problem A. Nezha Naohai
题目意思我不知道,但赛时我乱guess了一发a * b * c * d很不值得,不建议和我乱guess
#include<bits/stdc++.h>
using namespace std;
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using i64 = unsigned long long;
using i32 = unsigned;
using i128 = unsigned __int128;
#define all(x) (x).begin(), (x).end()
void solve(){
int a,b,c,d;
cin >> a >> b >> c >> d;
cout << (a + b + c ) * d << nl;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t = 1;
// cin >> t;
while(t--){
solve();
}
return 0;
}
Problem G. Exploration
赛时没做到这题,实际上非常简单
题意是有向图,然后有一个n个点和m条边,q个询问,对于每个询问有两个值u和x,u是出发点,x是初始的耐力。
当经过一条路过后,耐力值就会除以这条边的困难程度d。然后求对于询问的每个出发点和耐力,最少经过多少条边。
那么我们注意到他的数据范围,d最小为2,x最大为1e9,那么就是int32的范围,所以最多经过32条边,然后对每条边进行动态规划,记录最多32次所有路径上困难值之积,当这个积大于耐力值时就是肯定能走到0。
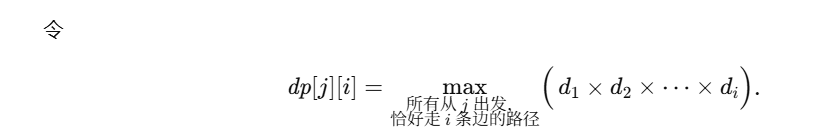
#include<bits/stdc++.h>
using namespace std;
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using i64 = unsigned long long;
using i32 = unsigned;
using i128 = unsigned __int128;
const ll inf = 1e9 + 7;
#define all(x) (x).begin(), (x).end()
void solve(){
int n,m,q;
cin >> n >> m >> q;
vector<vector<int>> adj(n + 1);
vector<vector<ll>> w(n + 1);
for(int i = 0;i < m;i++){
int u,v;
ll d;
cin >> u >> v >> d;
adj[u].push_back(v);
w[u].push_back(d);
}
vector<vector<ll>> dp(n + 1,vector<ll>(32));
for(int i = 1;i <= n;i++){
dp[i][0] = 1;
}
for(int i = 1;i < 32;i++){
for(int j = 1;j <= n;j++){
for(int k = 0;k < adj[j].size();k++){
dp[j][i] = max(dp[j][i],dp[adj[j][k]][i - 1] * w[j][k]);
}
dp[j][i] = min(inf,dp[j][i]);
}
}
while(q--){
int u;
ll x;
cin >> u >> x;
cout << upper_bound(dp[u].begin() + 1,dp[u].end(),x ) - dp[u].begin() << nl;
}
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t = 1;
// cin >> t;
while(t--){
solve();
}
return 0;
}
Problem I. Dating Day
题意大概是给一个字符串值(只包含0和1)和以及一个k,对于每个包含k个1的区间进行重新排序,问有多少种排序后的结果,然后对998244353进行取模
就是对每个区间进行组合。
#include<bits/stdc++.h>
using namespace std;
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using i64 = unsigned long long;
using i32 = unsigned;
using i128 = unsigned __int128;
#define all(x) (x).begin(), (x).end()
template<class T>
constexpr T power(T a, i64 b) {
T res = 1;
for (; b; b /= 2, a *= a) {
if (b % 2) {
res *= a;
}
}
return res;
}
constexpr i64 mul(i64 a, i64 b, i64 p) {
i64 res = a * b - i64(1.L * a * b / p) * p;
res %= p;
if (res < 0) {
res += p;
}
return res;
}
template<i64 P>
struct MLong {
i64 x;
constexpr MLong() : x{} {}
constexpr MLong(i64 x) : x{norm(x % getMod())} {}
static i64 Mod;
constexpr static i64 getMod() {
if (P > 0) {
return P;
} else {
return Mod;
}
}
constexpr static void setMod(i64 Mod_) {
Mod = Mod_;
}
constexpr i64 norm(i64 x) const {
if (x < 0) {
x += getMod();
}
if (x >= getMod()) {
x -= getMod();
}
return x;
}
constexpr i64 val() const {
return x;
}
explicit constexpr operator i64() const {
return x;
}
constexpr MLong operator-() const {
MLong res;
res.x = norm(getMod() - x);
return res;
}
constexpr MLong inv() const {
assert(x != 0);
return power(*this, getMod() - 2);
}
constexpr MLong &operator*=(MLong rhs) & {
x = mul(x, rhs.x, getMod());
return *this;
}
constexpr MLong &operator+=(MLong rhs) & {
x = norm(x + rhs.x);
return *this;
}
constexpr MLong &operator-=(MLong rhs) & {
x = norm(x - rhs.x);
return *this;
}
constexpr MLong &operator/=(MLong rhs) & {
return *this *= rhs.inv();
}
friend constexpr MLong operator*(MLong lhs, MLong rhs) {
MLong res = lhs;
res *= rhs;
return res;
}
friend constexpr MLong operator+(MLong lhs, MLong rhs) {
MLong res = lhs;
res += rhs;
return res;
}
friend constexpr MLong operator-(MLong lhs, MLong rhs) {
MLong res = lhs;
res -= rhs;
return res;
}
friend constexpr MLong operator/(MLong lhs, MLong rhs) {
MLong res = lhs;
res /= rhs;
return res;
}
friend constexpr istream &operator>>(istream &is, MLong &a) {
i64 v;
is >> v;
a = MLong(v);
return is;
}
friend constexpr ostream &operator<<(ostream &os, const MLong &a) {
return os << a.val();
}
friend constexpr bool operator==(MLong lhs, MLong rhs) {
return lhs.val() == rhs.val();
}
friend constexpr bool operator!=(MLong lhs, MLong rhs) {
return lhs.val() != rhs.val();
}
};
template<>
i64 MLong<0LL>::Mod = i64(1E18) + 9;
template<int P>
struct MInt {
int x;
constexpr MInt() : x{} {}
constexpr MInt(i64 x) : x{norm(x % getMod())} {}
static int Mod;
constexpr static int getMod() {
if (P > 0) {
return P;
} else {
return Mod;
}
}
constexpr static void setMod(int Mod_) {
Mod = Mod_;
}
constexpr int norm(int x) const {
if (x < 0) {
x += getMod();
}
if (x >= getMod()) {
x -= getMod();
}
return x;
}
constexpr int val() const {
return x;
}
explicit constexpr operator int() const {
return x;
}
constexpr MInt operator-() const {
MInt res;
res.x = norm(getMod() - x);
return res;
}
constexpr MInt inv() const {
assert(x != 0);
return power(*this, getMod() - 2);
}
constexpr MInt &operator*=(MInt rhs) & {
x = 1LL * x * rhs.x % getMod();
return *this;
}
constexpr MInt &operator+=(MInt rhs) & {
x = norm(x + rhs.x);
return *this;
}
constexpr MInt &operator-=(MInt rhs) & {
x = norm(x - rhs.x);
return *this;
}
constexpr MInt &operator/=(MInt rhs) & {
return *this *= rhs.inv();
}
friend constexpr MInt operator*(MInt lhs, MInt rhs) {
MInt res = lhs;
res *= rhs;
return res;
}
friend constexpr MInt operator+(MInt lhs, MInt rhs) {
MInt res = lhs;
res += rhs;
return res;
}
friend constexpr MInt operator-(MInt lhs, MInt rhs) {
MInt res = lhs;
res -= rhs;
return res;
}
friend constexpr MInt operator/(MInt lhs, MInt rhs) {
MInt res = lhs;
res /= rhs;
return res;
}
friend constexpr istream &operator>>(istream &is, MInt &a) {
i64 v;
is >> v;
a = MInt(v);
return is;
}
friend constexpr ostream &operator<<(ostream &os, const MInt &a) {
return os << a.val();
}
friend constexpr bool operator==(MInt lhs, MInt rhs) {
return lhs.val() == rhs.val();
}
friend constexpr bool operator!=(MInt lhs, MInt rhs) {
return lhs.val() != rhs.val();
}
};
template<>
int MInt<0>::Mod = 998244353;
template<int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();
constexpr int P = 998244353;
using Z = MInt <P>;
struct Comb
{
int n;
vector<Z> _fac;
vector<Z> _invfac;
vector<Z> _inv;
Comb() : n{0}, _fac{1}, _invfac{1}, _inv{0} {}
Comb(int n) : Comb()
{
init(n);
}
void init(int m)
{
if (m <= n)
return;
_fac.resize(m + 1);
_invfac.resize(m + 1);
_inv.resize(m + 1);
for (int i = n + 1; i <= m; i++)
{
_fac[i] = _fac[i - 1] * i;
}
_invfac[m] = _fac[m].inv();
for (int i = m; i > n; i--)
{
_invfac[i - 1] = _invfac[i] * i;
_inv[i] = _invfac[i] * _fac[i - 1];
}
n = m;
}
Z fac(int m)
{
if (m > n)
init(2 * m);
return _fac[m];
}
Z invfac(int m)
{
if (m > n)
init(2 * m);
return _invfac[m];
}
Z inv(int m)
{
if (m > n)
init(2 * m);
return _inv[m];
}
Z A(int a, int b)
{
if (a < b or b < 0)
return 0;
return fac(a) * invfac(a - b);
}
Z C(int n, int m)
{
if (n < m || m < 0)
return 0;
return fac(n) * invfac(m) * invfac(n - m);
}
} comb;
const int inf = 998244353;
void solve(){
int n,k;
cin >> n >> k;
string s;
vector<int> a;
cin >> s;
for(int i = 0;i < n;i++){
if(s[i] == '1') a.push_back(i + 1);
}
if(a.size() < k){
cout << 0 << nl;
return;
}
Z ans = 0;
for(int i = 0 ;i + k - 1 < a.size();i++){
int l = (i == 0 ? 0 : a[i - 1]);
int r = (i + k - 1 == a.size() - 1 ? n + 1 : a[i + k]);
ans += comb.C(r - l - 1,k);
if(r != n + 1){
ans -= comb.C(r - a[i] - 1,k - 1);
}
}
cout << ans << nl;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t = 1;
cin >> t;
while(t--){
solve();
}
return 0;
}
Problem K. Rotation
题意是有一排n个石像,石像最初始的位置为0-3,分别表示上下左右,然后现在有两种操作
第一种是让一个石像不动,让所有石像同时顺时针转动90度,第二种是使所有石像同时转动90度
这题其实就是相邻两个方向合并一共四种发现然后暴力找就行了,但是还是有点恶心人,赛场上读假了一次,想错了一次
#include<bits/stdc++.h>
using namespace std;
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using i64 = unsigned long long;
using i32 = unsigned;
using i128 = unsigned __int128;
#define all(x) (x).begin(), (x).end()
void solve(){
int n;
cin >> n;
vector<int> cnt(4);
for(int i = 0;i < n;i++){
int x;
cin >> x;
cnt[x]++;
}
int ans = INT_MAX;
for(int i = 0;i < 4;i++){
int res = cnt[i] + cnt[(i + 1) % 4] * 2 + cnt[(i + 2) % 4] * 3;
// cout << res << nl;
int m = (res + i + 3) % 4;
// cout << 4 - m << nl;
if(m != 0)
ans = min(ans,res + 4 - m);
else ans = min(ans,res);
}
cout << ans << nl;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t = 1;
// cin >> t;
while(t--){
solve();
}
return 0;
}
Problem M. Divide coins
这题是省二队友犯罪题,题意是有一排n个硬币初始面朝上,然后玩家二随意将其中k个硬币翻转向下
然后你作为玩家一有四种操作:
1.将硬币直接放入第一堆
2.将硬币翻转后放入第一堆
3.将硬币放入第二堆
4.将硬币翻转后放入第二堆
如果经过这些操作两堆硬币中的向上的硬币相等则你赢了
答案其实很简单就是翻转前n - k个硬币
但这题是我a完k后看的,然后蓝桥省二队友对我一通乱吼,说肯定是除了k等于0或者k等于n以外是没有答案的输出-1,然后我一开始还没看懂题目意思了,喜提好多罚时还很晚才a出来,md真的红温了
然后我看懂题目一看,n = 2,k = 1不就是有解的吗,然后顺着往下推就能发现规律,我只能说带菜的队友来捣乱还真不如不带
#include<bits/stdc++.h>
using namespace std;
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using i64 = unsigned long long;
using i32 = unsigned;
using i128 = unsigned __int128;
#define all(x) (x).begin(), (x).end()
void solve(){
int n,m;
cin >> n >> m;
for(int i = 0;i < n - m;i++){
cout << 2;
}
for(int i = 0 ;i < m;i++){
cout << 3;
}
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t = 1;
// cin >> t;
while(t--){
solve();
}
return 0;
}
Problem D. Virtuous Pope
阅读理解题,这题队伍翻译了两小时还没翻译出来,但是题目本身巨简单,把我赛场上急得团团转直跺脚,雅思爷雅思原来这么水的吗!
题目背景是花京院大战dio然后发现dio替身秘密的那一段,但是题目中那个攻击点我看不懂英文感觉真的很神秘啊,队友翻译的什么狗屎啊,队友看不懂这个立体几何毕竟是雅思爷不会练这种题的,然后给我翻译什么输入的x1,y1,z1形成一个平面,然后我和他说这肯定是条线,回去重新翻译又和我说可以无限延长到题目中的abc,就是边界位置,队友的翻译恶心死我了
最后我guess了一下是不是线线垂直,经过验证好像不太是,然后又看了一下我就大概看懂但是攻击点在哪没看懂,然后看到样例解释上都是x轴的又guess了一下,可惜没猜到是任意平行于坐标轴的平面
理解完题目赛后6分钟秒出,气死我了
#include<bits/stdc++.h>
using namespace std;
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using i64 = unsigned long long;
using i32 = unsigned;
using i128 = unsigned __int128;
#define all(x) (x).begin(), (x).end()
void solve(){
int n;
ll a,b,c;
cin >> n >> a >> b >> c;
map<ll,ll> mx,my,mz;
for(int i = 0 ;i < n;i++){
ll x1,y1,z1,x2,y2,z2;
cin >> x1 >> y1 >> z1 >> x2 >> y2 >> z2;
if(x2 < x1) swap(x2,x1);
if(y2 < y1) swap(y2,y1);
if(z2 < z1) swap(z2,z1);
mx[x1]++;
mx[x2 + 1]--;
my[y1]++;
my[y2 + 1]--;
mz[z1]++;
mz[z2 + 1]--;
}
ll mxmi = 0;
ll res = 0;
for(auto [x,y] : mx){
res += y;
mxmi = max(res,mxmi);
}
res = 0;
for(auto [x,y] : my){
res += y;
mxmi = max(res,mxmi);
}
res = 0;
for(auto [x,y] : mz){
res += y;
mxmi = max(res,mxmi);
}
cout << mxmi << nl;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t = 1;
// cin >> t;
while(t--){
solve();
}
return 0;
}
Problem F. Caloric Difference
纯纯看懂题目套公式
在这里我又要拷打我的队友了
拷打狠狠拷打
#include<bits/stdc++.h>
using namespace std;
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using i64 = unsigned long long;
using i32 = unsigned;
using i128 = unsigned __int128;
#define all(x) (x).begin(), (x).end()
void solve(){
int n,k;
cin >> n >> k;
ld r0,c0,l,r;
ld p;
cin >> r0 >> c0 >> p >> l >> r;
map<int,ld> mp;
for(int i = 0;i < k;i++){
int x;
ld y;
cin >> x >> y;
mp[x] = y;
}
ld ans = 0;
ld c = p * c0 + (1 - p ) * r0;
ans += c;
ld t = 0;
if(mp[1]) t = mp[1];
else t = l;
ans -= t;
for(int i = 2;i <= n;i++){
c = p * c + (1 - p) * t;
ans += c;
if(mp[i]) t = mp[i];
else t = l;
ans -= t;
}
cout << fixed << setprecision(10) << ans << nl;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t = 1;
cin >> t;
while(t--){
solve();
}
return 0;
}
总结
今年的题目难度总体来说其实和去年的江西省赛差不多,但各支队伍表现得不是很理想,好像都卡英文上了,听说这个是主办方要求的,于是我队伍翻译不出题目打铁了,md一个混子一个看不懂题目的雅思爷我就算再牛也得打铁啊,玉玉了
但总体体验还是很好的,见到了很多群u和大神,打a真的很快乐,如果有牌子就更快乐了


 浙公网安备 33010602011771号
浙公网安备 33010602011771号