动态规划 --- 理解背包问题

使用动态规划的条件：

1.最优化原理（最优子结构性质） 一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质使我们可以自底向上的方式从子问题的最优解逐步构造出整个问题的最优解。最优化原理是动态规划的基础，任何问题，如果失去了最优化原理的支持，就不可能用动态规划方法计算

若路线I和J是A到C的最优路径，则根据最优化原理，路线J必是从B到C的最优路线。（摘自gdut计院课件）

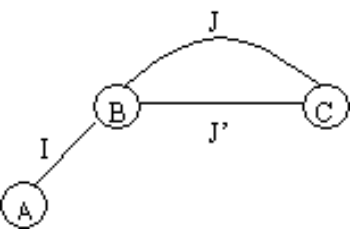
2.无后向性：将各阶段按照一定的次序排列好之后，对于某个给定的阶段状态，它以前各阶段的状态无法直接影响它未来的决策，而只能通过当前的这个状态。换句话说，每个状态都是过去历史的一个完整总结。这就是无后向性，又称为无后效性。

3.子问题的重叠性(非必要条件) 该条件为非必要条件，但是缺少此条件，则动态规划方法与别的方法相比毫无优势。每次产生的子问题并不是新的子问题，有些子问题被重复计算。 在解某一问题中，相同的子问题反复出现，并且不同子问题的个数又相对较少时，用动态规划是有效的。

动态规划实质上是一种以空间换时间的技术，它在实现的过程中，不得不存储产生过程中的各种状态，所以它的空间复杂度要大于其它的算法。

背包问题：给定n个重量为w1，….wn、价值为v1,……,vn的物品和一个承重量为W的背包，求这些物品中最有价值的一个子集，并且要能够装到背包中

数组元素BestSolution[i][j] 的意义是对于给定的前i个元素，在背包容量为j的时候的最大价值。

假设:

有4个物品，我们可以从 “往背包里加第0个物品” --》“往背包里加第0个和第1个物品” --》“往背包里加第0个和第1个和第2个物品” ... 到全部加入

大的问题可以由小的问题得出解：

对于当前的第i个物品，给定背包容量为package：

先判断：

我能不能把这个物品加入背包，即物品是否大于背包最大容量 -------》如果物品直接大于背包最大容量，那么就不能加入背包，最大价值和没有这个物品的时候一样(BestSolution[ i ][ package ] = BestSolution[ i-1 ][ package ])

如果我能够把这个物品放入背包，那么我是放进去好呢( value[i-1] + BestSolution[ i-1 ][ Package-weight [ i-1 ] ] )，还是不放进去( BestSolution[ i-1][ Package ] )好呢？这里就要取两种情况的最大值.

上代码:

import java.util.Scanner;
 
public class Solution {
    public static void main(String args[]) {
        Scanner sc = new Scanner(System.in);
        while(sc.hasNext()) {
            int n = sc.nextInt();
             
            int value[] = new int[n];
            int weight[] = new int[n];
             
             
            for(int i=0;i<n;i++) {
                value[i] = sc.nextInt();
            }
            for(int i=0;i<n;i++) {
                weight[i] = sc.nextInt();
            }
             
            int Package = sc.nextInt();
             
            //BestSolution[i][j] 表示 从 数组前 i个物品中选择，容量为j的背包的最大价值
            //行号表示物品数量，列号表示背包容量
            int BestSolution[][] = new int[n+1][Package+1];
             
            //第一列所有元素都是0，因为背包容量为0
            for(int i=0;i<=n;i++) {
                BestSolution[i][0] = 0;
            }
            //第一行所有列都是0，因为没有物品
            for(int i=0;i<=Package;i++) {
                BestSolution[0][i] = 0;
            }
             
            for(int i=1;i<=n;i++) {
                for(int j=1;j<=Package;j++) {
                    //对于当前背包容量，当前物品是否装得下
                    //如果背包装得下
                    if(weight[i-1]<=j) {
                                                              
                        BestSolution[i][j] = Math.max(
                                //当前物品不装进去
                                BestSolution[i-1][j],
                                <strong>//当前物品装进去
                                value[i-1]+BestSolution[i-1][j-weight[i-1]]);;</strong>
                    }else {
                        //装不下就和没有的最优解一样
                        BestSolution[i][j] = BestSolution[i-1][j];
                    }
                }
            }
             
            System.out.println("最大价值为:"+BestSolution[n][Package]);
        }
    }
}