DS博客作业06--图
1.2谈谈你对图结构的认识及学习体会
图中的顶点关系比树的更加复杂,不再是单纯的层次关系,而是平等的,点与点都可能连通,所以存储就需要模拟一个平面,在图的关系比较稀疏是用邻接表(使用线性存储),反之使用邻接矩阵,二维数据即可表示出一个平面。图的问题,主要是遍历和路径,难点在于找到相应算法(或者多种算法结合),解决一些实际问题时一般都会对算法进行相应的改动。
2.PTA实验作业
2.1.题目1:7-7 旅游规划
有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。
输入格式:
输入说明:输入数据的第1行给出4个正整数N、M、S、D,其中N(2≤N≤500)是城市的个数,顺便假设城市的编号为0~(N−1);M是高速公路的条数;S是出发地的城市编号;D是目的地的城市编号。随后的M行中,每行给出一条高速公路的信息,分别是:城市1、城市2、高速公路长度、收费额,中间用空格分开,数字均为整数且不超过500。输入保证解的存在。
输出格式:
在一行里输出路径的长度和收费总额,数字间以空格分隔,输出结尾不能有多余空格。
输入样例:
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
输出样例:
3 40
2.1.1设计思路
此题就是找最短路径,可以使用Dijkstra,使用一个包括距离和价钱的结构体建图,然后比较时优先考虑距离其次到价格。
结构体:
typedef struct
{
int weight=INF;//距离
int cost=INF;//价格
}VNode;
伪代码:
int main()
{
cin >> N >> M >> S >> D;
输入城市数量,和高速路和出发点、目的地
for (i = 0 to M)
{
cin >> x >> y >> w >> c;
读入高速路信息
graph[x][y].weight = graph[y][x].weight = w;//距离
graph[x][y].cost = graph[y][x].cost = c;//价格
}
调用Dijkstra(S, D);
return 0;
}
Dijkstra(S, D);函数
void Dijkstra(int v,int d)
{
VNode dist[501];//记录最短路径
int k;
int s[501] = { 0 };//S[i]=1表示顶点i在S中,S[i]=0表示顶点i在u中
VNode mindis;
for (i = 0 to N)//N个顶点
{
dist[i].weight = graph[v][i].weight;//距离初始化
dist[i].cost = graph[v][i].cost;//价格初始化
}
s[v] = 1;
for (i = 0 to N - 1)
{
mindis.weight = INF 初始化为最大值
for (j = 0 toj < N)
{
if (s[j] == 0 && dist[j].weight <= mindis.weight)如果j属于u中(没有被选)并且距离小于等于最小值
{
if (dist[j].weight < mindis.weight)距离小于最小值
{
k = j;
mindis.weight = dist[j].weight;
mindis.cost = dist[j].cost;
把该顶点信息记录
}
else if(dist[j].cost < mindis.cost)距离相等,比较价格
{
k = j;
mindis.cost = dist[j].cost;
把该顶点信息记录
}
}
}
s[k] = 1;
for (j = 0 to N)
{
if(j点属于u(没有被选过))
if(如果k和j连通)
if (graph[k][j].weight + dist[k].weight < dist[j].weight)如果过k点到j点的新路径比原来短
{
dist[j].weight = graph[k][j].weight + dist[k].weight;更新为短路径
dist[j].cost = graph[k][j].cost + dist[k].cost;
}
else if(graph[k][j].weight + dist[k].weight == dist[j].weight)
{
if (graph[k][j].cost + dist[k].cost < dist[j].cost)如果过k点到j点的新路径比原来便宜
{
dist[j].cost = graph[k][j].cost + dist[k].cost;更新为新价格
}
}
}
}
输出最短路径和价格
}
2.1.2代码截图



2.2.3本题PTA提交列表说明

Q:

看错题目然后误以为是输出目的地和价格,然后以为是bug找半天.。。。(还能过一个是最骚的),仔细看题目发现是输出路径的长度和价格
2.2.题目2:7-6 修建道路
N个村庄,从1到N编号,现在请您兴建一些路使得任何两个村庄彼此连通。我们称村庄A和B是连通的,当且仅当在A和B之间存在一条路,或者存在一个存在C,使得A和C之间有一条路,并且C和B是连通的。
已知在一些村庄之间已经有了一些路,您的工作是再兴建一些路,使得所有的村庄都是连通的,并且兴建的路的长度是最小的。
输入格式:
第一行是一个整数N(3<=N<=100),代表村庄的数目。后面的N行,第i行包含N个整数,这N个整数中的第j个整数是第i个村庄和第j个村庄之间的距离,距离值在[1,1000]之间。
然后是一个整数Q(0<=Q<=N*(N+1)/2)。后面给出Q行,每行包含两个整数a和b(1<=a<b<=N),表示在村庄a和b之间已经兴建了路。
输出格式:
输出一行仅有一个整数,表示为使所有的村庄连通需要新建公路的长度的最小值。
输入样例:
3
0 990 692
990 0 179
692 179 0
1
1 2
输出样例:
179
2.2.1设计思路
此题要求是修建公路使得任何两个村庄都有路到达并且是最短,对于题中提到村庄之间已经有公路,只需把此类村庄的距离当做0即可。然后通过prim生成最小生成树
注意:为了简单起见此题邻接矩阵的0并非常规prim算法中代表已经加入U(标记为选过),而是代表距离为0,标记则由visite[i]完成。
int main()
{
for (i=1 to N)
{
for (j = 1 to N)
{
读入村庄之间的距离到矩阵中
}
}
for (i = 0 to q)
{
读入已经修有路的村庄
graph[a][b] = graph[b][a]=0设置距离为零
}
调用prim函数
输出最小修路长度
return 0;
}
prim函数
int Prim(int v)
{
for (i = 1 to N)N个村庄
{
对lowcost和closest数组初始化
lowcost[i] = graph[v][i]距离
closest[i] = v路径
}
visite[v] = 1标记已经加入U
for (i = 1 to N)
{
for (j = 1 to N)
{
查找lowcost中未加入U(即visite[j]=0)最小的点
用k记录
}
找到后把距离累加到sum中
把该点标记已经加入U
for (int j = 1; j <= N; j++)
{
修改lowcost和closet
if (visite[j]== 0 && graph[k][j] < lowcost[j])如果通过k到未选的点有短的距离
{
lowcost[j] = graph[k][j];
closest[j] = k;
}
}
}
返回return sum;
}
2.2.2代码截图


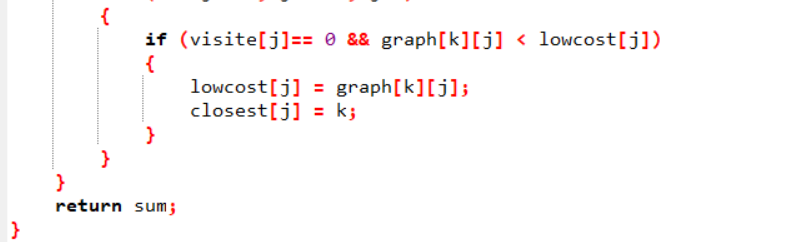
2.2.3本题PTA提交列表说明

A:两个wa,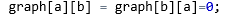 是此处之前没有两个置为0(无向图),
是此处之前没有两个置为0(无向图),
2.3.题目3:7-3 六度空间
六度空间”理论又称作“六度分隔(Six Degrees of Separation)”理论。这个理论可以通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过五个人你就能够认识任何一个陌生人。”如图1所示。
假如给你一个社交网络图,请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。
输入格式:
输入第1行给出两个正整数,分别表示社交网络图的结点数N(1<N≤10
4
,表示人数)、边数M(≤33×N,表示社交关系数)。随后的M行对应M条边,每行给出一对正整数,分别是该条边直接连通的两个结点的编号(节点从1到N编号)。
输出格式:
对每个结点输出与该结点距离不超过6的结点数占结点总数的百分比,精确到小数点后2位。每个结节点输出一行,格式为“结点编号:(空格)百分比%”。
输入样例:
10 9
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
输出样例:
1: 70.00%
2: 80.00%
3: 90.00%
4: 100.00%
5: 100.00%
6: 100.00%
7: 100.00%
8: 90.00%
9: 80.00%
10: 70.00%
2.3.1设计思路
此题有点的像树的层次遍历,使用queue辅助搜索,visite[i]标记已经认识过的人,然后通过广度优先搜索,把所有人都认识完或者已经达到第六层(最多通过五个人认识)就可以结束搜索。
图结构体
typedef struct
{
int **edgs;(直接声明数组会爆)
double n, e;
}MatGraph;
int main()
{
为邻接矩阵分配内存,直接声明会爆
for (i = 0 to M)邻接矩阵初始化
{
int x, y;
cin >> x >> y;
G.edgs[x][y] = G.edgs[y][x] = 1;
}
for (i = 1 to N)调用N次广搜
{
调用BFS(G, i);
}
delete内存
return 0;
}
void BFS(MatGraph G,int v)
{
使用cur表示当前访问的顶点 ,last表示该层次的最后一个顶点
当cur==last声明该层次遍历结束
while (!q.empty()&&level<6)//队空或者层数到6
{
从队列去队头元素 temp =cur= q.front();
for (int i = 1; i <=G.n; i++)
{
if (G.edgs[temp][i] != 0 && visite[i] == 0)寻找通过当前点可以认识其他点
{
visite[i] = 1;标记已认识
q.push(i);入队
sum++;认识人数
}
}
if (cur == last)//遍历一层结束
{
if (!q.empty())
{
last = q.back();
level++;
}
}
}
printf("%d: %.2f%%\n",v,sum*100 / (G.n));输出结果
}
2.3.2代码截图



2.3.3本题PTA提交列表说明

A:直接过了,注意下层次和标记就可以了,
3、上机考试错题及处理办法(-2--2分)
3.1.截图错题代码
3.1.1题目:六度空间
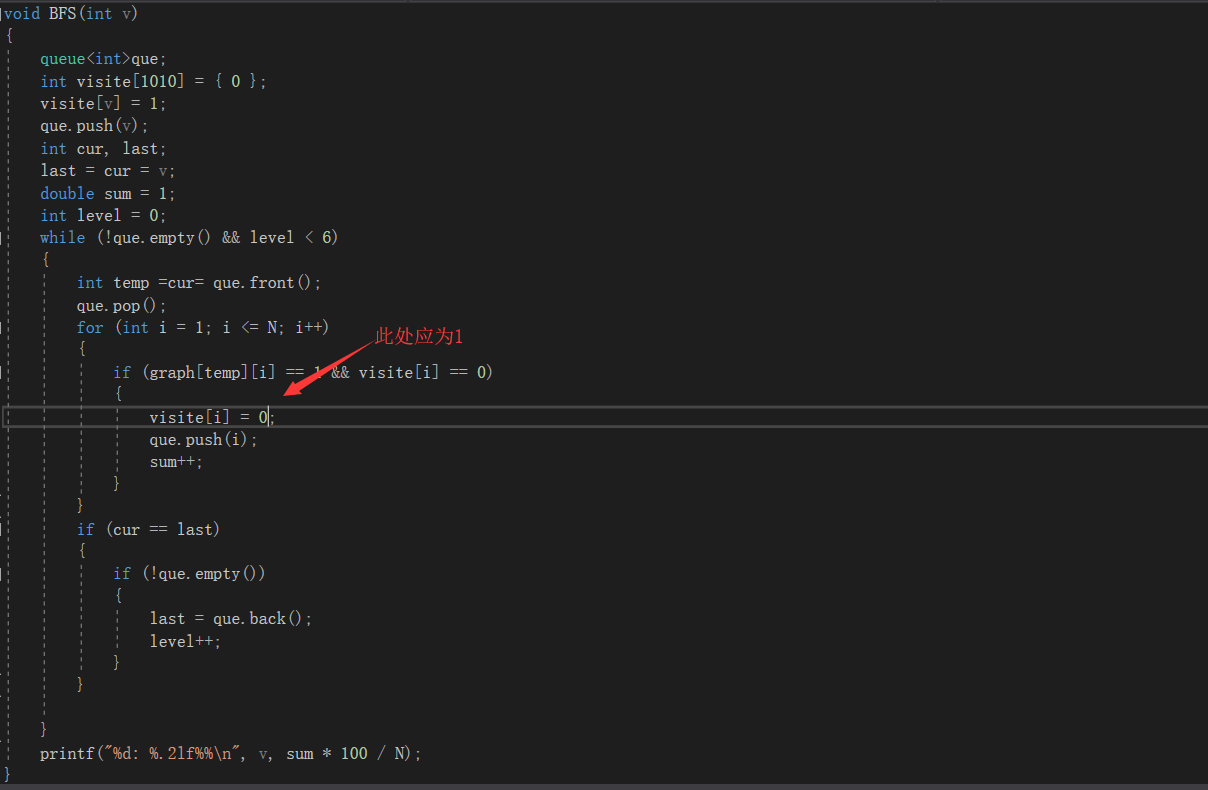
3.2 错的原因及处理方法
visite[i]等于1才是标记为已选,但是打错,然后编译器一直提示的是内存爆了,我以为是数组问题,后来才发现是该处错误引发的无限循环。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号