记力扣股票题的动态规划思考

所有题目可以直接点击跳转到力扣

1、买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

 

此题可以直接贪心，找队列中后减前的最大值，但是此时该考虑的是动态规划

 

天数与当天价格作为列，第一行应该是从未买过股票的金钱，因为不买不卖，所以恒为0

dp [ i ] [ 0 ] = 0;

 

第二行则是在某一天买入时，手上钱的最大值，当然是负数，而且是从未买过股票在今天买的价钱 0 - price [ i ]

dp [ i ] [ 1 ] = max { dp [ i - 1 ] [ 1 ] , dp [ i - 1 ] [ 0 ] - price[ i ] }

 

第三行则是在当天卖出会有多少钱，当然选择在当天之前购买股票时持有最多的前，在当天卖出才能赚的最多

dp [ i - 1 ] [ 2 ] 中则会保存在当天之前曾经赚到的最多的钱，只有在赚的更多的时候才会更新第三行中的值

dp [ i ] [ 2 ] = max { dp [ i - 1 ] [ 2 ] , dp [ i - 1 ] [ 1 ] + price[ i ] }

因为 dp [ i ] [ 2 ] 总会保存 i 天中能赚的最多的钱，因此直接输出 dp [ i ] [ 2 ] 就行

 

2、买卖股票的最佳时机 II

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

 

因为同时只能持有一股，在当天买入卖出没有意义，因此又是贪心，每次在之前能用更低价钱买入，在当天能卖出时，都赚钱

作为贪心来看，只要昨天价钱更低，就可以在昨天买入今天卖出，如果明天价钱更高，则在今天买入明天卖出，然而考虑动态规划

此题与上题不同，因为可以买任意次，因此每次赚到钱，都可以当成第一次买股票之前持有的金钱

由于当天买股票之前的钱应该是昨天能持有的最大现金，因此像上一题的第一行是没有意义的

 

dp [ i ] [ 0 ] 中保存当天持有彩票的最大金钱，昨天与之前持有彩票的最大值与昨天卖出彩票后持有的金钱在今天购买彩票中的最大值

dp [ i - 1 ] [ 0 ]　　今天之前持有彩票时的最大金钱

dp [ i - 1 ] [ 1 ] - price[ i ] 　　昨天之前卖出彩票后持有的金钱在今天购买彩票后的值

dp [ i ] [ 0 ] = max { dp [ i - 1 ] [ 0 ] , dp [ i - 1 ] [ 1 ] - price[ i ] }

 

dp [ i ] [ 1 ] 中保存能够获得的最大金钱

dp [ i ] [ 0 ] + price [i] 　　当天卖掉彩票能获得多少钱 ——> max { dp [ i - 1 ] [ 0 ] + price [ i ] , dp [ i - 1 ] [ 1 ] }

dp [ i - 1 ] [ 1 ] 　　在之前的某一天卖掉彩票能保持多少钱

dp [ i ] [ 1 ] = max { dp [ i ] [ 0 ] + price [i] , dp [ i - 1 ] [ 1 ] }　　dp [ i ] [ 0 ] 是根据前一天的的数据计算的，因此可以把条件全部换成昨天的

再观察 dp [ i ] [ 1 ] 与 dp [ i ] [ 0 ] ，很明显只要今天的股票价值比昨天高，dp [ i ] [ 1 ]就该等于 dp [ i - 1 ] [ 0 ] + price [ i ] ，低的话之前就该把股票卖了

dp [ i ] [ 1 ] = max { dp [ i - 1 ] [ 0 ] + price [ i ] , dp [ i - 1 ] [ 1 ] }

 

3、买卖股票的最佳时机 III

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

 

用贪心来看，应该找前两个能获取最大利润的点，但情况就复杂了，如 [ 1, 5, 2, 6 ]，看似最大是 5，实际上取了 5 就无法取两个 4 了

此时该用动态规划实现

明显类似于第一题，则第一行应该和第一题一样全是0

dp [ i ] [ 0 ] = 0;

 

第二行与第三行都是第一题的模样

dp [ i ] [ 1 ] = max { dp [ i - 1 ] [ 1 ] , dp [ i - 1 ] [ 0 ] - price[ i ] }

dp [ i ] [ 2 ] = max { dp [ i - 1 ] [ 2 ] , dp [ i - 1 ] [ 1 ] + price[ i ] }

 

前三行一定能找到最大利润点，那么怎么用动态规划获取第二大的利润点呢？

其实很多文章都有写，是模仿第二和第三行，但是我始终没有看懂，这也是我写这篇随笔的原因，记录一下自己的思考过程

dp [ i ] [ 3 ] = max { dp [ i - 1 ] [ 3 ] , dp [ i - 2 ] [ 2 ] - price[ i ] }

dp [ i ] [ 4 ] = max { dp [ i - 1 ] [ 4 ] , dp [ i - 3 ] [ 1 ] + price[ i ] }

根据公式写点数据看看情况，可以看到结果确实是 11 ，在1到8之外第二高利润点为4

 

 

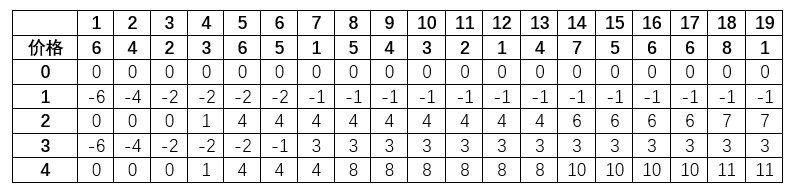
在第五列，第三行与第五行同时获取了最大利润点，在之后如果吧第三、四、五行都减4，就像是将第六列当做第一列的一、二、三行

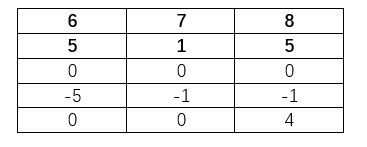
 二、三行因为第一行全为 0 ，因此第三行只保留最大的利润，四、五行会同步二、三行的最大利润，并找到小于等于该利润的次高利润

第五行在第八列变成 8 了，因为在 7 买 8 买  有大于利润为 4 ，那么在第二行找到更大值时是怎么更新第五行呢

稍微对数据修改一下，看看找次高利润和更新最高利润的区别

 

 

 

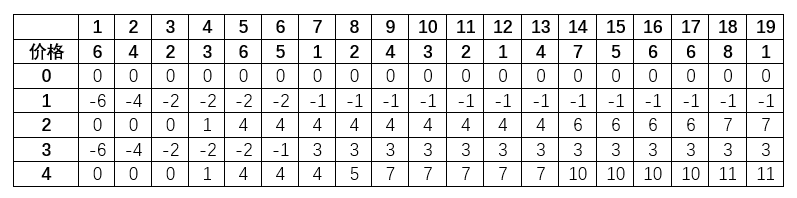
 突然发现下一个能更新最高利润的股票价钱是由二、三行决定的，当 -2 和 4 的时候是 4 - ( - 2 ) ，当找到更低点时是 4 - ( - 1 ) = 5

第五列第二行的 - 2 是最佳购入点，而第四行则是 4 - 6 = -2 ，该最大点才是最佳购入点

在第一次找到最大点之前，价格减去昨天能持有的最大金钱总是第二行的数值，因此第四行才与第二行有相同的数字

比如第五列，实际上该点相当于 - 6，然后三、四、五行全部加 4 ，因此看起来是 - 2

从第六列开始，四、五行才发挥作用，到13列之前增加次高点 3 ，将整张动态规划表拆开看更能体现

 

 

 

 

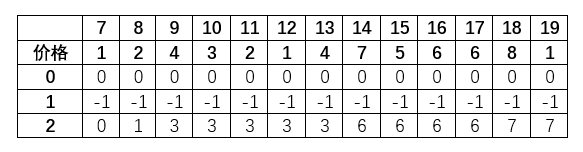
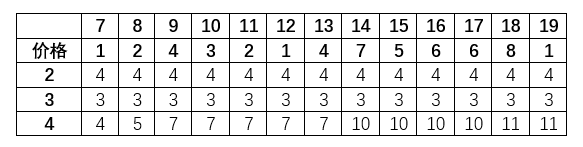
一、二、三从 0 开始寻找更大值，三、四、五从当前最大值寻找更大值，找到的较小值也不放过

不是第一次买入和第二次买入，在公式上很像，实际是一、二、三将极大值传给三、四、五，再与之一起寻找另一个较大值

当较大值不足以更新一、二、三时，则只会更新三、四、五，当足够更新最大值时，则两方一起更新，且三、四、五以极大值为底更新

 

若是背公式，则当成第一次购买与第二次购买好记，然而其中的真实情况令人着迷，此时我只是暂时说服自己

 

4、买卖股票的最佳时机 IV

用贪心则是记录所有单次购买的利润，最后降序排序取前k个，若不足k个全部取

与第三题一样，二、三找最大，四、五找次大，并且与二、三一起更新更大，k层中没有传递更大值，而是以上一层为底更新更大值

将第零列的 1,2 称为第一层，以此类推，方便叙述也方便理解

第一层找单次买卖的最大利润，第二层找两次买卖的最大利润，k 层找 k 次买卖的最大利润

可惜，这些说法都无法说服我自己，还得填数据分析，令 k = 3 

 

 

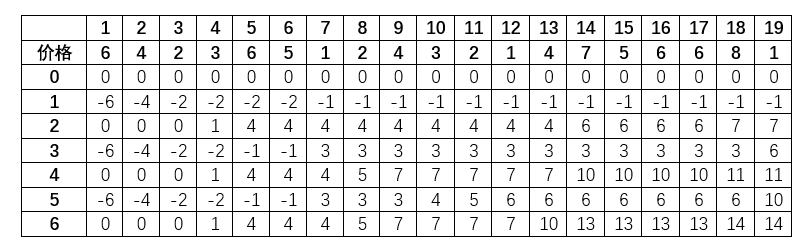
和预想的一样，在找到第二个利润点前，第二层与第三层一起增加，直到第三个利润点出现才产生不同

还有相同点，开始产生不同的由持有股票行先变化，就像是找最低点，然后找到最低点后卖出股票行变化，找最高点

我决定第一题的 dp [ i  ] [ 2 ] 不要替换其中的 dp [ i ] [ 1 ]

dp [ i ] [ 0 ] = 0　　　未购买过

dp [ i  ] [ 1 ] = max { dp [ i ] [ 0 ] - price [ i ] , dp [ i - 1 ] [ 1 ] }          当天第一次买入或之前买入取最大

dp [ i  ] [ 2 ] = max { dp [ i ] [ 1 ] + price [ i ] , dp [ i - 1 ] [ 2 ] }         当天第一次卖出或之前就卖出了取最大

dp [ i  ] [ 3 ] = max { dp [ i ] [ 2 ] - price [ i ] , dp [ i - 1 ] [ 3 ] }          当天第二次买入，此时是拿着第一次卖出的钱购买，或延续之前

dp [ i  ] [ 4 ] = max { dp [ i ] [ 3 ] + price [ i ] , dp [ i - 1 ] [ 4 ] }         当天第二次卖出，当然是第二次买入才能第二次卖出，或延续之前

在吃饭时突然想通了与其想购买卖出，不如思考为什么更新上一层时，下层的增长与上层一致

 

动态规划　　　每一层的尝试都是将自身较小的值变成较大值，当为 0 时看似是一样的，实际上不一样，并且很巧妙的将相同起点的值在遍历中自动取最大值了

更妙的是当上层被更新时，下层一定会被更新，而下层的更新若无法影响上层，更无法更新更高层，是单向传递的

动规第一层　　[ 4 ]　    　  [ 4 ] 　　      [ 7 ]

动规第二层　　[ 4, 0 ]　    　[ 4, 3 ]　　   [ 4, 7 ]

动规第三层　　[ 4, 0, 0 ]　    　[ 4, 3, 0 ]　　 [ 4, 3, 7 ]

因此第一层与其说是第一次买卖最大，不如说是单次买卖最大，第二层则是两次买卖最大，而不是所谓的当天第一次和第二次购买

再回头看第一层与第二层，当第一层增大到7时，第二层卖出后的最大金钱为11，刚好需要利润大于4时才能更新

此处我虽然理解了，但是无法用语言表达清楚，留于后日更新　　————2023.3.15

 

5、最佳买卖股票时机含冷冻期

给定一个整数数组prices，其中第  prices[i] 表示第 i 天的股票价格 。​

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

 

在这一题贪心就有点吃力了，因为不能把连续的多个利润合成最大利润了

如 [ 1 , 2 , 3 , 1 , 3 ] ，没有冷冻期直接记 2 ，2，相加就好，有冷冻期则要记 [ 1 , 3 ] 为 [ 1 , 1 ] ，[ 4 , 5 ] 为 [ 2 ] 

当两个区段相连时，要么前一个区段去尾，要么后一个区段去头，而且区段内只有一个时该值要大于上个相邻区段尾和下个相邻区段头，要处理的就太多了

 

冷冻期相当于限制了买股票，不能昨天卖出今天买，只能前天卖出今天买，dp [ i ] [ 0 ] 中保存当天持有彩票的最大金钱

dp [ i - 1 ] [ 0 ]　　今天之前持有彩票时的最大金钱

dp [ i - 2 ] [ 1 ] - price[ i ] 　　昨天之前卖出彩票后持有的金钱在今天购买彩票后的值

dp [ i ] [ 0 ] = max { dp [ i - 1 ] [ 0 ] , dp [ i - 2 ] [ 1 ] - price[ i ] }

 

dp [ i ] [ 1 ] 中保存能够获得的最大金钱，卖出股票不受冷冻期影响

dp [ i ] [ 0 ] + price [i] 　　当天卖掉彩票能获得多少钱 ——> max { dp [ i - 1 ] [ 0 ] + price [ i ] , dp [ i - 2 ] [ 1 ] }

dp [ i - 1 ] [ 1 ] 　　在之前的某一天卖掉彩票能保持多少钱

dp [ i ] [ 1 ] = max { dp [ i ] [ 0 ] + price [i] , dp [ i - 1 ] [ 1 ] }　　dp [ i ] [ 0 ] 是根据以前的数据计算的，但替换后需要比较三个值大小，不如不更换

dp [ i ] [ 1 ] = max { dp [ i ] [ 0 ] + price [i] , dp [ i - 1 ] [ 1 ] }

如果没有冷冻期

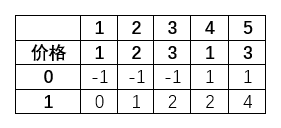
 加上冷冻期

 

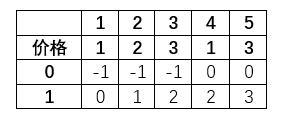
 要我说这题比三四题更容易思考，仅仅是计算当天持有彩票时进行了变化，其他文章中冷冻期行只是为了把前天的数据搬到昨天，那样所有计算数据都是昨天提供的

 

总结

 动态规划真神秘