CF870E题解

题目大意

给你平面上 \(n(1\leqslant n \leqslant 10^5)\) 个点，给出他们的坐标 \(x_i,y_i(-10^9\leqslant x_i,y_i \leqslant 10^9)\)。

对于每个点有三种操作：不进行任何操作、过这个点作一条平行于 \(x\) 轴的直线、过这个点作一条平行于 \(y\) 轴的直线。

问能够形成多少种不同的平面。

思路分析

个人认为这道题思维难度还是比较大的，比较难想。

首先很显然的一点，因为每个有三种状态，那么答案的上限就是 \(3^n\)，即每一行每一列仅有不超过一个点，没有任何两个点在同一行或同一列。

然后我们有一个比较清奇的思路，就是将每个点的 \(x,y\) 坐标拆成一个 \(x\) 轴上的点和一个 \(y\) 轴上的点，每个 \(x\) 轴上的点要么不操作，要么画平行于 \(y\) 轴的线，每个 \(y\) 轴上的点要么不操作，要么画平行于 \(x\) 轴的线，那么这就形成了一个天然的二分图，然后将点对应的的 \(x,y\) 坐标连边。

举个例子：

\((1,2),(1,4),(3,2),(3,4)\) 四个点，那么图建出来就是这个样子：

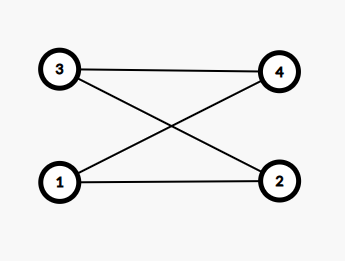
左边表示 \(x\) 坐标，右边表示 \(y\) 坐标。

然后我们以这种方式建完图后，会发现形成了许多连通块，那么根据乘法原理，我们只需要统计每个连同块内的的答案，再累乘起来就行了。

现在我们看一看如何求每个连通块内的答案，先放结论：

设 \(tot\) 为连通块内点的数量，\(cnt\) 为边的数量，那么有

\[ans= \left\{\begin{array}{ll}2^{tot}(cnt\geqslant tot)\\2^{tot}-1(cnt+1=tot)\end{array}\right. \]

然后我们来分析一下结论中的两种情况：

• \(cnt+1=tot\)

如下图：

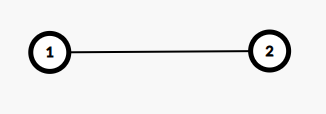
理论上来说，每个点有两种情况，那么答案应该是 \(2^{tot}\)，但仔细想一下，我们是把一个点拆开来了，那么就不可能左边的点选择画竖线的同时右边的点画横线，所以要减一。

那么我们可以换个思考方式，因为我们图里的每一条边代表的是一个平面直角坐标系内的坐标，所以我们可以将每一个点的方案放到它所连接的边上，那么这里不管我们 \(1\) 点或 \(2\) 点放在边上，都有一个点无法放上边，那么就要减一。

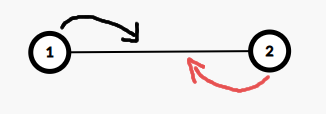
• \(cnt \geqslant tot\)

同上面例子：

这种形成环的情况下，很显然每个点都能够成功的放到一条边上去，并且不会重边，所以答案就是 \(2^{tot}\)。

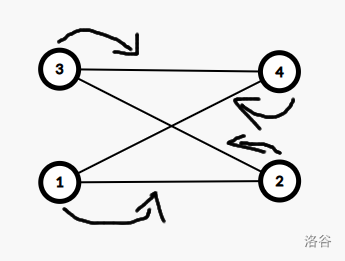
代码实现只需要用并查集这种及其基础的知识点，二分图只是用在思想上，代码就不放了，很简单。