[LeetCode] 1504. Count Submatrices With All Ones
Given an m x n binary matrix mat, return the number of submatrices that have all ones.
Example 1:
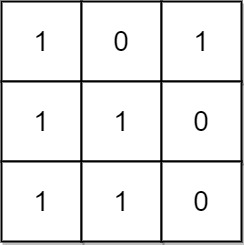
Input: mat = [[1,0,1],[1,1,0],[1,1,0]]
Output: 13
Explanation:
There are 6 rectangles of side 1x1.
There are 2 rectangles of side 1x2.
There are 3 rectangles of side 2x1.
There is 1 rectangle of side 2x2.
There is 1 rectangle of side 3x1.
Total number of rectangles = 6 + 2 + 3 + 1 + 1 = 13.
Example 2:
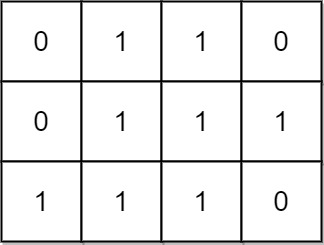
Input: mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]]
Output: 24
Explanation:
There are 8 rectangles of side 1x1.
There are 5 rectangles of side 1x2.
There are 2 rectangles of side 1x3.
There are 4 rectangles of side 2x1.
There are 2 rectangles of side 2x2.
There are 2 rectangles of side 3x1.
There is 1 rectangle of side 3x2.
Total number of rectangles = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24.
Constraints:
1 <= m, n <= 150
mat[i][j] is either 0 or 1.
统计全 1 子矩形。
给你一个 m x n 的二进制矩阵 mat ,请你返回有多少个 子矩形 的元素全部都是 1 。
思路
思路是单调栈。做法类似84题和85题。
首先我们还是需要创建一个 heights 数组来记录矩阵里每个 j 位置上的高度。高度的定义是从当前行往上数,连续的1的个数。
把矩阵按行向下累计为“高度数组” h[j]:若 mat[i][j]==1,则 h[j]++,否则清零。对于每一行的 h,计算以该行作为底边、且右端点在每一列 j的全 1 子矩阵数量之和。这个子问题等价于:在柱状图 h 中,统计以每个位置 j 作为右端点的矩形个数并求和。
用单调递增栈求解上一步:维护一个 sum[j] 表示“以 j 为右端点”的子矩阵数量。
- 若栈空:sum[j] = h[j] * (j + 1)
- 若有前一个更小柱高 prev:sum[j] = sum[prev] + h[j] * (j - prev)
最后把本行所有 sum[j] 累加到答案。
复杂度
时间O(m * n^2)
空间O(n)
代码
Java实现
class Solution {
public int numSubmat(int[][] mat) {
int m = mat.length;
int n = mat[0].length;
int[] h = new int[n];
int res = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (mat[i][j] == 1) {
h[j]++;
} else {
h[j] = 0;
}
}
res += helper(h);
}
return res;
}
private int helper(int[] h) {
int res = 0;
int n = h.length;
// 以 j 为右端点的矩形个数
int[] sum = new int[n];
// sum[j] = 以 j 为右端点的矩形数
Deque<Integer> stack = new ArrayDeque<>();
for (int j = 0; j < n; j++) {
while (!stack.isEmpty() && h[j] <= h[stack.peekLast()]) {
stack.pollLast();
}
if (stack.isEmpty()) {
// 左边没有更小的柱子,宽度可延伸到 0..j
sum[j] = h[j] * (j + 1);
} else {
int prev = stack.peekLast();
// 继承到 prev 的贡献 + 以高度 h[j] 向左延伸 (j - prev) 列的新矩形
sum[j] = sum[prev] + h[j] * (j - prev);
}
stack.offerLast(j);
res += sum[j];
}
return res;
}
}
相关题目
84. Largest Rectangle in Histogram
85. Maximal Rectangle
221. Maximal Square
1277. Count Square Submatrices with All Ones
1504. Count Submatrices With All Ones
1727. Largest Submatrix With Rearrangements



 浙公网安备 33010602011771号
浙公网安备 33010602011771号