[LeetCode] 1260. Shift 2D Grid

Given a 2D grid of size m x n and an integer k. You need to shift the grid k times.

In one shift operation:

• Element at grid[i][j] moves to grid[i][j + 1].
• Element at grid[i][n - 1] moves to grid[i + 1][0].
• Element at grid[m - 1][n - 1] moves to grid[0][0].

Return the 2D grid after applying shift operation k times.

Example 1:

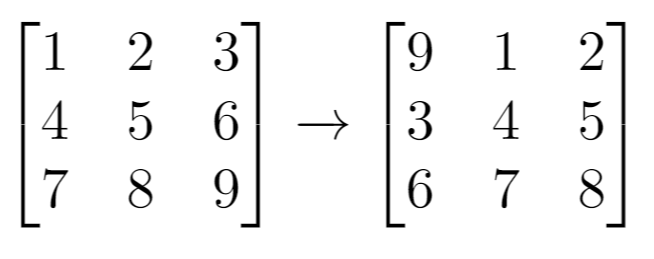
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
Output: [[9,1,2],[3,4,5],[6,7,8]]

Example 2:

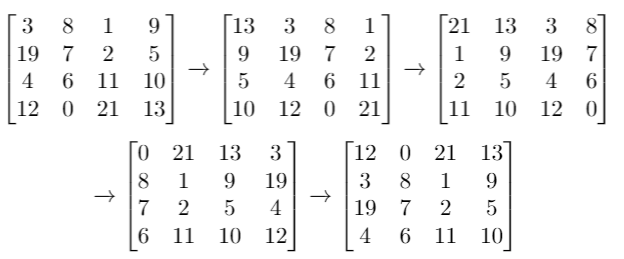
Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

Example 3:

Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
Output: [[1,2,3],[4,5,6],[7,8,9]]

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m <= 50
• 1 <= n <= 50
• -1000 <= grid[i][j] <= 1000
• 0 <= k <= 100

二维网格迁移。

给你一个 m 行 n 列的二维网格 grid 和一个整数 k。你需要将 grid 迁移 k 次。

每次「迁移」操作将会引发下述活动：

位于 grid[i][j] 的元素将会移动到 grid[i][j + 1]。
位于 grid[i][n - 1] 的元素将会移动到 grid[i + 1][0]。
位于 grid[m - 1][n - 1] 的元素将会移动到 grid[0][0]。
请你返回 k 次迁移操作后最终得到的 二维网格。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/shift-2d-grid
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

一开始审题的时候，直观感觉这个题很像54题那一类 matrix 的题型，一直在想有没有不用额外空间或者原地修改 matrix 的做法。首先我给一个朴素的解法，需要用到额外空间。思路是先遍历 matrix，把每个元素按顺序放入一个双端队列 deque 中。将 K % mn 之后，把元素再按序放到 list。最后输出的是 list of list。

时间O(mn)

空间O(n) - queue

Java实现

class Solution {
    public List<List<Integer>> shiftGrid(int[][] grid, int k) {
        int m = grid.length;
        int n = grid[0].length;
        List<List<Integer>> res = new ArrayList<>();
        Deque<Integer> queue = new ArrayDeque<>();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                queue.add(grid[i][j]);
            }
        }
        for (int i = 0; i < k; i++) {
            queue.addFirst(queue.pollLast());
        }
        for (int i = 0; i < m; i++) {
            List<Integer> temp = new ArrayList<>();
            for (int j = 0; j < n; j++) {
                temp.add(queue.poll());
            }
            res.add(new ArrayList<Integer>(temp));
        }
        return res;
    }
}

 

不使用 deque 的方法如下。因为结果集是 list of list，所以并不涉及到去挪动 matrix 中的元素，对每个 sublist 里面的元素，我们只需要精确找到他在原来 matrix 里的起始位置就可以了。首先 K 还是要去模一下 matrix 的总长度 mn，这样就知道 K 到底在 matrix 的什么位置。同时需要把这个二维坐标转换成一维的，这样便于计算。16 行的减 K 相当于是去找原 matrix 中前 K 个位置上的那个元素。

时间O(mn)

空间O(1)

Java实现

class Solution {
    public List<List<Integer>> shiftGrid(int[][] grid, int k) {
        List<List<Integer>> res = new ArrayList<>();
        int m = grid.length;
        int n = grid[0].length;
        int total = m * n;
        k %= m * n;
        for (int i = 0; i < m; i++) {
            res.add(new ArrayList<>());
        }
        
        for (int i = 0; i < total; i++) {
            // 应该放的数字原来在的位置
            // 应该是后退了K步
            int position = (i - k + total) % total;
            res.get(i / n).add(grid[position / n][position % n]);
            // System.out.println(position);
        }
        return res;
    }
}

 

LeetCode 题目总结