[LeetCode] 1443. Minimum Time to Collect All Apples in a Tree

Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend in order to collect all apples in the tree starting at vertex 0 and coming back to this vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [fromi, toi] means that exists an edge connecting the vertices fromi and toi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple, otherwise, it does not have any apple.

Example 1:

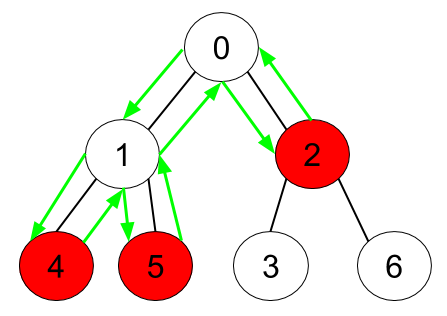
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], 
hasApple = [false,false,true,false,true,true,false]
Output: 8 
Explanation: The figure above represents the given tree where red vertices have an apple. 
One optimal path to collect all apples is shown by the green arrows.  

Example 2:

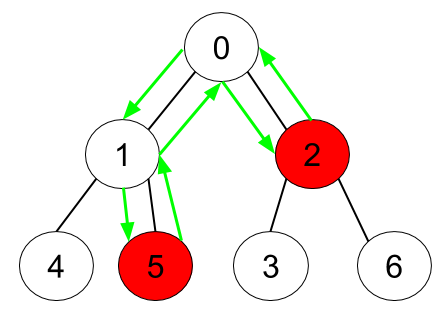
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], 
hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. 
One optimal path to collect all apples is shown by the green arrows.  

Example 3:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], 
hasApple = [false,false,false,false,false,false,false]
Output: 0

Constraints:

• 1 <= n <= 10^5
• edges.length == n-1
• edges[i].length == 2
• 0 <= fromi, toi <= n-1
• fromi < toi
• hasApple.length == n

收集树上所有苹果的最少时间。

给你一棵有 n 个节点的无向树，节点编号为 0 到 n-1 ，它们中有一些节点有苹果。通过树上的一条边，需要花费 1 秒钟。你从 节点 0 出发，请你返回最少需要多少秒，可以收集到所有苹果，并回到节点 0 。
无向树的边由 edges 给出，其中 edges[i] = [fromi, toi] ，表示有一条边连接 from 和 toi 。除此以外，还有一个布尔数组 hasApple ，其中 hasApple[i] = true 代表节点 i 有一个苹果，否则，节点 i 没有苹果。
来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/minimum-time-to-collect-all-apples-in-a-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题意是给一个树和几个参数，其中 n 表示树的节点个数，edges 代表每个节点之间的连接关系，hasApple 是一个 boolean 数组，表示每个节点上是否有苹果，请你返回如果从节点 0 开始找，需要花费多少时间找到所有苹果并返回节点 0。

discussion里面绝大部分的思路都是DFS，我的解法也不例外。我用到这么几个数据结构

• list of list - 创建邻接表
• boolean数组记录哪些node被遍历过了

先创建邻接表，这里注意虽然题目中说了是 tree 但是其实是一个多叉树，所以还是当做一个 graph 在处理。然后因为你是从 0 开始遍历所以在做 DFS 前，先把 0 标记为 visited。在 DFS 的时候，因为是多叉树所以要对每个 node 的 children list 做 for 循环，看每一个孩子节点是否有苹果。count 代表需要走几步，所以如果某个节点的孩子节点传上来的 count > 0 的话（表示下面有苹果），或者这个节点本身是有苹果的（hasApple.get(v) == true），那么就意味着一定需要走过去拿苹果，所以 count += 2。走两步是因为一来一回。

时间O(n)

空间O(n)

Java实现 - 2020年10月更新

class Solution {
    public int minTime(int n, int[][] edges, List<Boolean> hasApple) {
        List<List<Integer>> adj = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            adj.add(i, new ArrayList<>());
        }
        for (int[] e : edges) {
            adj.get(e[0]).add(e[1]);
            adj.get(e[1]).add(e[0]);
        }
        boolean[] visited = new boolean[n];
        visited[0] = true;
        return dfs(adj, hasApple, 0, visited);
    }

    private int dfs(List<List<Integer>> adj, List<Boolean> hasApple, int v, boolean[] visited) {
        if (adj.get(v) == null) {
            return 0;
        }
        int count = 0;
        List<Integer> children = adj.get(v);
        for (int child : children) {
            if (!visited[child]) {
                visited[child] = true;
                count += dfs(adj, hasApple, child, visited);
            }
        }
        if ((count > 0 || hasApple.get(v)) && v != 0) {
            count += 2;
        }
        return count;
    }
}

 

LeetCode 题目总结