CSP-S模拟31 笔记

T1 远征

\(O(nV)\) DP。先鸽。

T2 传送

题目描述

给定 \(n\) 点 \(m\) 边无向无自环图 \(G\) , \(q\)次询问，每次询问给定点 \(x\) , \(y\) ，求点 \(x\) , \(y\) 在图 $G^′ $ 上的距离。
图 \(G^′\) 的定义为：

1. $ \forall (a,b) \in G , (a,b) \in G^′. $
2. $ \forall (a,b),(b,c),(c,d) \in G^′, (a,d) \in G^′ . (a,b,c互不相同)$

此处 \(a,b\) 表示由点 \(a\) 与点 \(b\) 间的边。

保证 \(n,m,q<10^6\)

叟卢十

将 \(G^′\) 建出来再跑最短路绝对不可行。

我们将条件1提供的边即原图中的称为“基本边”，条件2提供的边称为“新加边”，

先考虑一条链的情况，如图所示：

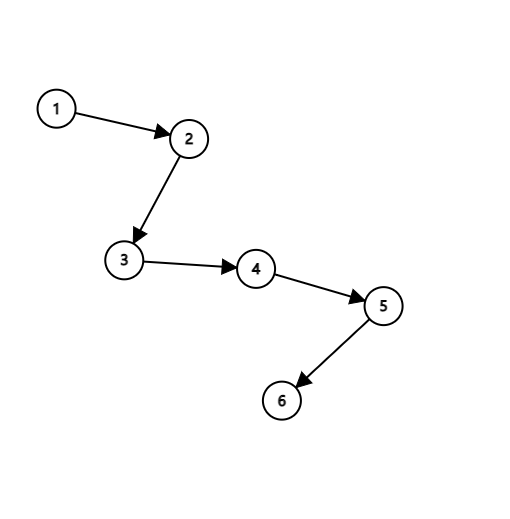
显然，当一条路径上有超过三条基本边或新加边时，这三条边可以被一条新加边替代。

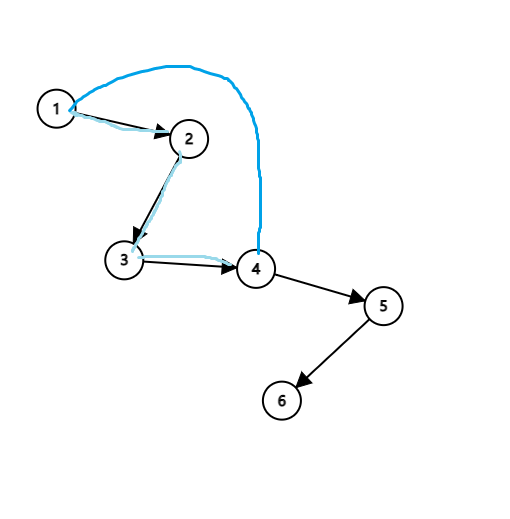
如图，\((1-2)(2-3)(3-4)\)（浅蓝色边）可以替换为 \((1,4)\) (深蓝色边)，\(1\) 到 \(6\) 的路径变为 \((1-4)(4-5)(5-6)\)

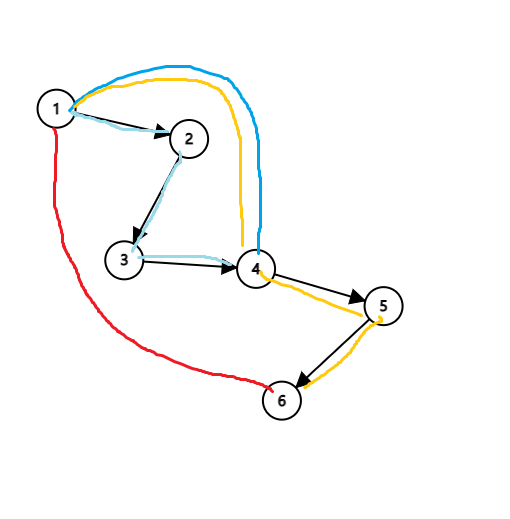
然后，\((1-4)(4-5)(5-6)\)（橘红色边）可以替换为 \((1,4)\) (深蓝色边)，\(1\) 到 \(6\) 的路径变为 \((1-6)\)

这是一个什么过程？

动用人类智慧思考后会发现，当路径长度超过3时，显然可以通过一条新加边让路径长度-2；

所以，当一条路径长度为奇数时。该路径可以被一条长度为1的路径替代。当一条路径长度为偶数时。该路径可以被一条长度为2的路径替代。

所以若联通的两点间可以找到一条长度为奇数的路径，则两点最近距离为1.否则最近距离为2.

问题转化为：两点间能否找到长度为奇数的路径？

当图为一条链时，显然一次dfs就可求得。复杂度 \(O(n)\)。

当图为一棵树时，如图：

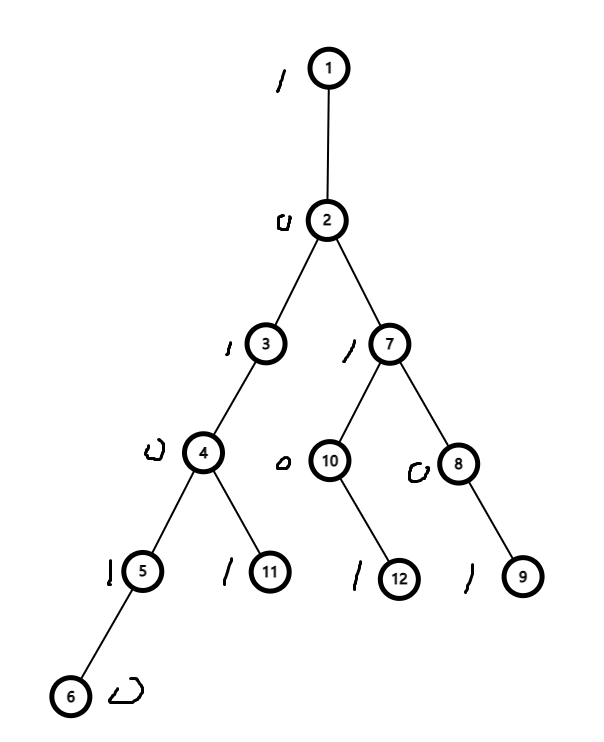
为每个节点标记模2意义下的深度，

发现该图中所有路径均为 \((0-1-0-1-0-1-...)\) 0,1交替

可得任意两深度相同（模2意义下）的点路径长度均为偶数，否则则为奇数

深度可dfs求出，复杂度 \(O(n)\)。

若图不为树：

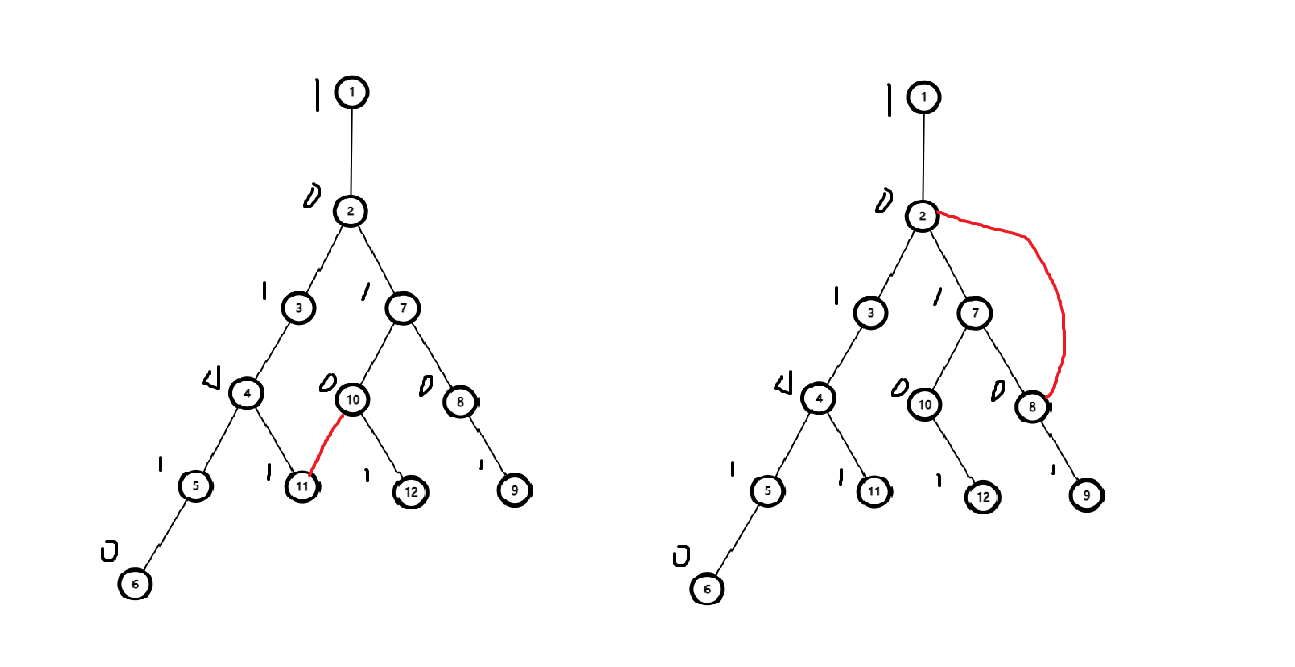
任何图都可看作一棵树加若干边构成。本图中以红色标记在树上增加的边。

左图中，增加的边为不同深度的点之间。加边后，图中路径仍然均为 \((0-1-0-1-0-1-...)\) 0,1交替，红色边不会对答案产生任何影响，可以直接忽略。

右图中，增加的边为相同深度的点之间。加边后，图中出现了不为0,1交替的路径！最短距离为1的点对不会受到影响。

但最短距离为2的点对（即深度相同的点对）之间可以通过经过一次红色边找到一条长度为奇数的路径。例如（4，9）之间，在加入红色边前（4,9）间所有路径长度均为偶数，但加入红色边后，可以找到路径（4-3-2-9）长度为奇数。则（4，9）间的最短距离由2变为1。可以证明，加入红色边后，任何点对间最短距离均为1。

得出结论：若一条非树边链接两个深度相同的点，则称该边为“好边”。任意“好边”所在联通块中所有点对距离均为1。

实际代码中，在dfs求深度时记录每个点所属连通块。若dfs访问到一条“好边”，则标记该连通块为“好块”。询问时，若两点所属连通块为“好块”，则直接输出1。

复杂度 \(O(n)\)

代码

点击查看代码

#include<bits/stdc++.h>
using namespace std;
inline int read()
{
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=(x<<1)+(x<<3)+(ch-'0');
		ch=getchar();
	}
	return x*f;
}
inline int max(int x,int y){return (x<y)?y:x;}
inline int min(int x,int y){return (x<y)?x:y;}
int n,m;
int h[1000005],to[2000005],nxt[2000005],tot;
int god[1000005];//是否为好块 
int dfn[1000005];//记录每个点所属连通块 
int dep[1000005];
void add(int x,int y){
	tot++;
	to[tot]=y;
	nxt[tot]=h[x];
	h[x]=tot;
}
void dfs(int x){
	int y=h[x];
	while(y){
		int t=to[y];
		y=nxt[y];
		if(dfn[t]){
			continue;
		}
		dfn[t]=dfn[x];
		dep[t]=dep[x]+1;
		dep[t]%=2;
		dfs(t);
	}
}
int main()
{
	freopen("teleport.in","r",stdin);
	freopen("teleport.out","w",stdout);
	read();
	n=read();
	m=read();
	for(int i=1;i<=m;i++){
		int x,y;
		x=read();
		y=read();
		add(x,y);
		add(y,x); 
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]){
			dfn[i]=i;
			dep[i]=1;
			dfs(i); 
		}
	}
	for(int i=1;i<=n;i++){
		int y=h[i];
		while(y){
			int t=to[y];
			y=nxt[y];
			if(dep[i]==dep[t]){
				god[dfn[i]]=1;
			}
		}
	} 
	int T;
	T=read();
	while(T--){
		int x,y;
		x=read();
		y=read();
		if(x==y){
			putchar('0');
			putchar('\n');
			continue;
		}
		if(dfn[x]!=dfn[y]){
			putchar('-');
			putchar('1');
			putchar('\n');
			continue;
		}
		if(dep[x]!=dep[y]||god[dfn[x]]){
			putchar('1');
			putchar('\n');
		}else{
			putchar('2');
			putchar('\n');
		}
	}
	return 0;
}

T3 先辈

\(O(26^2n)\)，鸽着

T4 矩阵

\(O(1)\) , 鸽着