关于使用二叉树结构存储计算表达式的专题讨论(网安2312陈卓)
关于使用二叉树结构存储计算表达式
日常生活中对于表达式的计算往往通过人力采取一定的计算技巧得出结果,而计算机中则采用不同算法解决该问题,其中一种采用二叉树结构存储计算表达式(表达式树)则是我们今天要讨论的类型。
表达式树
为了处理表达式而遵循相应规则构造的树被称为表达式树。
前缀,中缀,后缀表达式:
前缀表达式
前缀表达式是将运算符写在两个操作数之前的表达式。和后缀表达式一样,前缀表达式没有括号,运算符没有优先级,能严格按照从右到左的顺序计算。
中缀表达式
我们平时缩写的表达式,将运算符写在两个操作数中间的表达式,称作中缀表达式。在中缀表达式中,运算符有不同的优先级,圆括号用于改变运算顺序,这使得运算规则比较复杂,求值过程不能直接从左到右顺序进行,不利于计算机处理。
后缀表达式
将运算符写在两个操作数之后的表达式称作后缀表达式。后缀表达式中没有括号,并且运算符没有优先级。后缀表达式的求值过程能够严格按照从左到右的顺序进行,有利于计算机处理。
主要思路:
我们知道一个表达式的计算是按照优先级逐级计算的,而这种逐级分层的解决方式正好符合树的递归结构,因此我们可以将表达式的每一步运算视为一颗子树,再按照运算先后顺序将各个子树进行连接,则所得到的树即为该表达式的表达式树。例如表达式1+(2+3)*2-4/5,如图:
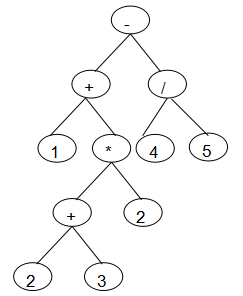
而如何通过代码实现树的构建,我们可以通过转换后的表达式辅助解决这一问题,先观察给定表达式(1+(2+3)*2-4/5)的三种表达方式:
前缀:- + 1 * + 2 3 2 / 4 5
中缀:1 + (2 + 3) * 2 - 4 / 5
后缀:1 2 3 + 2 * + 4 5 / -
我们发现前缀表达式和后缀表达式与表达式树之间存在一一对应的关系:
在前缀表达式中根结点为表达式的最后一位,表达式树按照先左后右的顺序从表达式末尾开始依次取值建立结点,当结点数据为运算符号时,将运算符号存入结点数据而后对其左右孩子进行结点的创建,当结点数据为运算数时,将运算数存入结点数据,之后返回上一级(运算数不能作为运算符号对其左右孩子的值进行运算),直到返回到根结点,创建结束;
与此类似,在后缀表达式中根结点也为表达式的最后一位,而相反的是表达式树是按照先右后左的顺序从表达式末尾开始依次取值建立结点,当结点数据为运算符号时,将运算符号存入结点数据而后对其左右孩子进行结点的创建,当结点数据为运算数时,将运算数存入结点数据,之后返回上一级,直到返回到根结点,创建结束。
接下来是代码的实现过程(本篇将根据后缀表达式创建表达式树):
二叉树的结构定义(具体代码):
typedef struct BiTNode {
char data;
struct BiTNode* lchild, * rchild;
}BTNode, * BTree;
中缀表达式转后缀表达式:
中缀转后缀要考虑运用栈(先进先出)辅助表达式的转换,从左到右依次对中缀表达式中的每个字符进行以下处理,直到表达式结束:
1.如果字符是运算数,则直接添加到后缀表达式的字符串中
2.如果字符是‘(’,将其入栈
3.如果字符是运算符,先将栈顶优先级不低于该运算符的运算符出栈,添加到后缀表达式中,再将该运算符入栈。注意,当‘(’在栈中时,优先级最低
4.如果字符是‘)’,将栈顶元素出栈,添加到后缀表达式中,直到出栈的是‘(’
5.如果表达式结束,但栈中还有元素,将所有元素出栈,添加到后缀表达式中
例如给定表达式:1+(2+3)*2-4/5,栈中元素和表达式的变化如下表所示:
| 当前要处理的字符 | 栈 | 后缀表达式 | 详细操作 |
|---|---|---|---|
| 1 | - | 1 | 将1加入表达式 |
| + | + | 1 | 将+入栈 |
| ( | + ( | 1 | 将(入栈 |
| 2 | + ( | 1 2 | 将2加入表达式 |
| + | + ( + | 1 2 | 将+入栈 |
| 3 | + ( + | 1 2 3 | 将3加入表达式 |
| ) | + | 1 2 3 + | 将+出栈,加入表达式 |
| * | + * | 1 2 3 + | 将*入栈 |
| 2 | + * | 1 2 3 + 2 | 将2加入表达式 |
| - | - | 1 2 3 + 2 * + | 将*和+依次出栈,加入表达式 |
| 4 | - | 1 2 3 + 2 * + 4 | 将4加入表达式 |
| / | - / | 1 2 3 + 2 * + 4 | 将/入栈 |
| 5 | - / | 1 2 3 + 2 * + 4 5 | 将5加入表达式 |
| 1 2 3 + 2 * + 4 5 / - | 将/和-依次出栈,加入表达式 |
具体代码如下(后缀表达式):
void InitExpTree(BTree& T, string str)
{
stack<char> s, s1; //定义两个空栈,s负责暂存转换过程中的运算符号,s1负责存储转换后的表达式
int i = 0;
while (str[i] != '\0')
{
if (str[i] >= '0' && str[i] <= '9')
{
s1.push(str[i]);
} //将数字直接加入表达式
else if (str[i] == '+' || str[i] == '-' || str[i] == '*' || str[i] == '/')
{
if (s.empty())
{
s.push(str[i]);
} //为空直接入栈
else if (str[i] == '+' || str[i] == '-')
{
if (s.top() == '*' || s.top() == '/') //判断当前运算符号与栈顶元素符号的优先级
{
while (!s.empty() && s.top() != '(')
{
s1.push(s.top());
s.pop();
}
} //当前运算符号优先级高则输出s中所有运算符号
s.push(str[i]);
}
else
{
s.push(str[i]);
}
}
else if (str[i] == '(')
{
s.push(str[i]);
}
else if (str[i] == ')')
{
while (s.top() != '(')
{
s1.push(s.top());
s.pop();
}
s.pop();
} //括号匹配,输出括号内运算符号
i++;
}
while (!s.empty())
{
s1.push(s.top());
s.pop();
} //表达式结束,输出s中剩余运算符号
}
后缀表达式转表达式树:
对于表达式树的创建则要采用递归思想:如果当前结点数据元素为运算数,则存储数据后return;否则存储数据后再依次递归右孩子和左孩子,如图:

具体代码如下(表达式树):
void ExpTree(BTree& T, stack<char>& s)
{
if (s.empty())
{
return;
} //栈为空则表达式树创建完毕
if (s.top() >= '0' && s.top() <= '9')
{
BTree e = new BTNode;
e->data = s.top();
s.pop();
e->lchild = NULL;
e->rchild = NULL;
T = e;
return;
} //如果数据为运算数,则存储后直接返回
T = new BTNode;
T->data = s.top();
T->lchild = NULL;
T->rchild = NULL;
s.pop();
ExpTree(T->rchild, s);
ExpTree(T->lchild, s); //如果数据为运算符号,则依次递归右孩子和左孩子创建结点
}
总体代码如下:
#include<iostream>
#include<stack>
#include<string>
#include<queue>
using namespace std;
typedef struct BiTNode {
char data;
struct BiTNode* lchild, * rchild;
}BTNode, * BTree;
void ExpTree(BTree& T, stack<char>& s)
{
if (s.empty())
{
return;
} //栈为空则表达式树创建完毕
if (s.top() >= '0' && s.top() <= '9')
{
BTree e = new BTNode;
e->data = s.top();
s.pop();
e->lchild = NULL;
e->rchild = NULL;
T = e;
return;
} //如果数据为运算数,则存储后直接返回
T = new BTNode;
T->data = s.top();
T->lchild = NULL;
T->rchild = NULL;
s.pop();
ExpTree(T->rchild, s);
ExpTree(T->lchild, s); //如果数据为运算符号,则依次递归右孩子和左孩子创建结点
}
void InitExpTree(BTree& T, string str)
{
stack<char> s, s1; //定义两个空栈,s负责暂存转换过程中的运算符号,s1负责存储转换后的表达式
int i = 0;
while (str[i] != '\0')
{
if (str[i] >= '0' && str[i] <= '9')
{
s1.push(str[i]);
} //将数字直接加入表达式
else if (str[i] == '+' || str[i] == '-' || str[i] == '*' || str[i] == '/')
{
if (s.empty())
{
s.push(str[i]);
} //为空直接入栈
else if (str[i] == '+' || str[i] == '-')
{
if (s.top() == '*' || s.top() == '/') //判断当前运算符号与栈顶元素符号的优先级
{
while (!s.empty() && s.top() != '(')
{
s1.push(s.top());
s.pop();
}
} //当前运算符号优先级高则输出s中所有运算符号
s.push(str[i]);
}
else
{
s.push(str[i]);
}
}
else if (str[i] == '(')
{
s.push(str[i]);
}
else if (str[i] == ')')
{
while (s.top() != '(')
{
s1.push(s.top());
s.pop();
}
s.pop();
} //括号匹配,输出括号内运算符号
i++;
}
while (!s.empty())
{
s1.push(s.top());
s.pop();
} //表达式结束,输出s中剩余运算符号
}
double EvaluateExTree(BTree T)
{
if (T->lchild == NULL && T->rchild == NULL)
{
double x;
x = (double)(T->data - '0');
return x;
} //判断当前结点是否为存储运算数的结点
double a, b;
a = EvaluateExTree(T->lchild);
b = EvaluateExTree(T->rchild); //按照从左到右的运算顺序计算
char e = T->data;
if (e == '+')
{
return a * 1.0 + b;
}
else if (e == '-')
{
return a * 1.0 - b;
}
else if (e == '*')
{
return a * 1.0 * b;
}
else if (e == '/')
{
if (b == 0)
{
cout << "divide 0 error!";
exit(0);
} //判断分母是否为零
else
{
return a * 1.0 / b;
}
}
return 0;
}
int main()
{
BTree T = NULL;
string s;
cin >> s;
InitExpTree(T, s);
double sum = 0;
sum = EvaluateExTree(T);
cout << sum; //输出该表达式树的运算结果
return 0;
}
运行结果如下(以1+(2+3)*2-4/5为例):

表达式树&直接使用栈计算表达式比较:
| 表达式树 | 直接使用栈 | |
|---|---|---|
| 时间复杂度 | O(n) | O(n) |
| 空间复杂度 | O(n) | O(n) |
由此可以看出,使用表达式树和直接使用栈来计算表达式在时间复杂度上没有显著差异,都是O(n)。在空间复杂度方面,两者也类似,都是O(n),但表达式树可能需要额外的空间来存储树结构。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号