Programe_Of_Beauty：3.8 求二叉树中节点的最大距离

1.问题定义

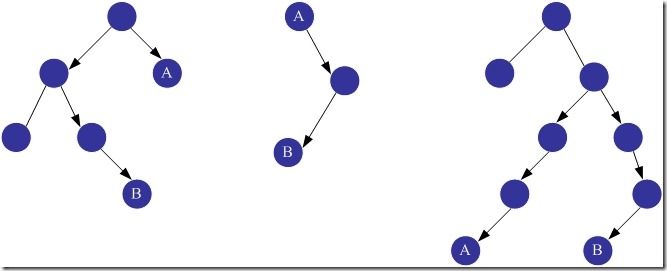
定义距离为两个节点之间边的个数。写一个程序求一棵二叉树中相距最远的两个节点之间的距离。下面是两个例子：

上图中列出了二叉树中节点间距离最大的所有可能情况。箭头所指的边标示了A、B之间最大的距离。

2.问题分析

从上图中可以看出，距离最远的两个点一定有一个共同的“根”节点，或者其中一个就是根节点(注意前者的“根”与后者的根的区别，前者的“根”包含后者)。因此只要能计算出所有“根”的左子树的最深长度和右子树的最深长度，就可以知道经过此“根”节点的所有路径中的最大距离。通俗的讲，就是计算任意一个节点的左右子树的最深长度。

3.递归算法

树节点的结构体定义：

struct _Node
{
	_Node * Lchild;
	_Node * Rchild;
	int     data;
};

定义一个全局变量，用来记录访问过的所有节点中的最大距离。

int MMax = 0;

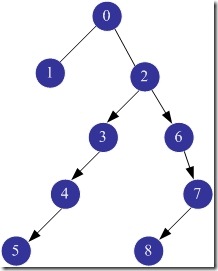
生成二叉树：

void HCreateTree()
{
	_NNode * root = new _NNode[9];
	for (int i = 0; i <9; i ++)
	{
		root[i].data = i;
		root[i].Lchild = NULL;
		root[i].Rchild = NULL;
	}
	root[0].Lchild = &root[1];
	root[0].Rchild = &root[2];
	root[2].Lchild = &root[3];
	root[2].Rchild = &root[6];

	root[3].Lchild = &root[4];
	root[4].Lchild = &root[5];

	root[6].Rchild = &root[7];
	root[7].Rchild = &root[8];
        FindMaxLen(root);//计算最大距离的函数
	cout<<"MMax="<<MMax<<endl;
	delete[] root;
}

上面代码构造的二叉树如图所示。

int FindMaxLen(_Node *root)
{
	if (root)
	{
		int i = FindMaxLen(root->Lchild);//返回当前节点root左子树的最深长度
		int j = FindMaxLen(root->Rchild);//返回当前节点root右子树的最深长度
		if ( (i + j) > MMax)//更新MMax
                   {
			MMax = i + j;
                   }
		if (i > j)
			return i + 1;
		else
			return j + 1;
	}
	return 0;
}

输出结果为6。当然你也可以参考《编程之美》3.8关于这个问题的求解。