数学建模多指标评价还在用【熵权+topsis】？6 种高级代替方案在这里！（附MATLAB 全搭建）

序章：一杯奶茶的选择难题

“生活中的每一次选择，都是对多个维度的权衡 —— 选奶茶时，我们要比价格、品甜度、看口感、评颜值；做项目决策时，要算成本、测效率、评风险、估收益。可如果只凭‘感觉’给每个维度定‘重要性’，或是死守一种评价方法，很可能错过最优解。”

你是否曾在数学建模中遇到这样的困境：用熵权 + TOPSIS 做评价时，要么因数据离散度太低导致权重失真（比如所有方案的 “成本” 指标几乎一样），要么因指标太多导致计算冗余，甚至因数据缺失而卡壳？今天我们先吃透熵权 + TOPSIS 的核心逻辑，再解锁 6 种更灵活的高级替代方案，让多指标评价从 “机械套用” 变成 “精准适配”。

基础篇：熵权 + TOPSIS—— 让数据自己 “定规矩”

在讲替代方案前，我们先搞懂 “熵权 + TOPSIS” 为什么是建模入门首选：它的核心是用数据客观定权重，用 “距离” 定优劣，完美解决了 “凭经验给权重” 的主观偏差问题。

1.1 核心痛点：为什么需要熵权 + TOPSIS？

假设我们要评选 “最佳奶茶店”，有 5 家店（方案），4 个评价指标（价格：越低越好；甜度：越适中越好，用 1-5 分；口感：越高越好；颜值：越高越好）。

若直接 “拍脑袋” 定权重（比如认为口感最重要，给 0.5 权重），会忽略数据本身的信息（比如价格差异极大，本应更受关注）；
若只看单一指标（比如只比口感），又会漏掉价格、颜值等关键维度。

熵权 + TOPSIS 的价值就在于：让数据的 “离散程度” 决定权重（熵权），让方案与 “理想状态” 的距离决定排名（TOPSIS）。

1.2 熵权 + TOPSIS 的 “三步法” 逻辑（附通俗类比）

步骤 1：数据标准化 —— 消除 “单位偏见”

不同指标的单位 / 量级不同（比如价格单位是 “元”，而口感却是评分），直接计算会让 “大数指标”（如价格 10-30 元）掩盖 “小数指标”（如甜度 1-5 分）。

标准化公式（以 “正向指标” 为例，越高越好）：\(x_{ij}' = \frac{x_{ij} - \min(x_j)}{\max(x_j) - \min(x_j)}\)（反向指标如价格，分子换为\(\max(x_j) - x_{ij}\)）
类比：把 “价格（10-30 元）” 和 “口感（1-5 分）” 都转换成 “0-1 分” 的统一尺度，就像把 “身高（cm）” 和 “体重（kg）” 都换成 “BMI 指数” 对比一样。

步骤 2：熵权法算权重 —— 让 “差异大的指标更重要”

熵权的本质是 “用信息熵衡量指标的离散度”：

信息熵公式：\(e_j = -\frac{1}{\ln n} \sum_{i=1}^n p_{ij} \ln p_{ij}\)（\(p_{ij} = \frac{x_{ij}'}{\sum_{i=1}^n x_{ij}'}\)，避免\(\ln 0\)需加微小值）
权重公式：\(w_j = \frac{1 - e_j}{\sum_{j=1}^m (1 - e_j)}\)
类比：如果 5 家奶茶店的价格全是 15 元（离散度为 0，\(e_j=1\)），说明 “价格” 没法区分好坏，权重\(w_j=0\)；如果价格从 10 元到 30 元差别大（离散度高，\(e_j\)小），说明 “价格”这个指标对于奶茶的“好坏”影响很大，是一个很关键的指标，权重\(w_j\)就大。

步骤 3：TOPSIS 算贴近度 —— 找 “最接近理想方案的那个”

TOPSIS 的思路是：先找一个 “理想方案”（每个指标都是最优值）和 “最劣方案”（每个指标都是最差值），再算每个方案到这两个方案的 “欧氏距离”，贴近度越近理想方案，排名越靠前。

加权标准化矩阵：\(z_{ij} = w_j \cdot x_{ij}'\)（给每个指标加权重）
理想方案：\(Z^+ = (\max(z_{1j}), \max(z_{2j}), ..., \max(z_{mj}))\)
最劣方案：\(Z^- = (\min(z_{1j}), \min(z_{2j}), ..., \min(z_{mj}))\)
贴近度：\(C_i = \frac{d_i^-}{d_i^+ + d_i^-}\)（\(d_i^+\)是到理想方案的距离，\(d_i^-\)是到最劣方案的距离）
类比：把每个奶茶店看作一个点，“理想店” 是 “最便宜、最甜、口感最好、颜值最高” 的点，算每个店到这个点的距离，离得越近越优。

1.3 熵权 + TOPSIS 的局限 —— 为什么需要替代方案？

对数据要求高：若指标数据离散度极低（如所有方案的 “风险” 指标都一样），熵权会趋近于 0，导致该指标被 “忽略”；
无法融入主观经验：比如行业专家明确认为 “效率比成本重要”，但熵权法只看数据，会违背专业判断；
处理模糊指标无力：遇到 “用户满意度”“服务质量” 这类无法精确量化的指标，熵权 + TOPSIS 难以处理；
指标冗余时计算繁琐：若有 10 个以上高度相关的指标（如 “成本”“费用”“开销”），会导致信息重复，排名失真。

进阶篇：6 种高级替代方案 —— 精准适配不同场景

针对熵权 + TOPSIS 的局限，我们按 “场景需求” 分类，给出 6 种替代方案，每种方案都附 “生活类比 + 核心逻辑 + 适用场景 + MATLAB 代码”。

方案 1：AHP+TOPSIS—— 主观经验 + 客观数据双保险

场景类比：

选奶茶时，先让奶茶师（专家）定 “口感> 颜值 > 价格 > 甜度” 的大致顺序（主观权重），再用各店的实际数据算贴近度（客观排名），既不瞎猜，也不忽视专业经验。

核心逻辑：

AHP（层次分析法）：通过 “专家 pairwise 比较”（比如 “口感比价格重要多少”）构建判断矩阵，算主观权重，同时做 “一致性检验”（避免专家前后矛盾，如 “口感 > 价格” 且 “价格 > 口感”）；
TOPSIS：沿用之前的逻辑，但用 “AHP 主观权重 + 熵权客观权重” 的加权和（如主观占 0.6，客观占 0.4）作为最终权重，兼顾经验与数据。

适用场景：

有行业专家参与、需要融合主观判断的评价（如项目立项、产品评优）。

方案 2：灰色关联分析（GRA）—— 数据少、信息不全也能评

场景类比：

新开了 3 家奶茶店，只有 1 周的销售数据（数据少、信息不全），没法算熵权（离散度不够），但能通过 “各店数据与理想数据的‘相似度’” 排序 —— 比如 “理想店” 日销 100 杯，A 店 80 杯、B 店 70 杯、C 店 60 杯，A 店与理想店的 “关联度” 最高。

核心逻辑：

灰色关联分析不追求 “精确的权重”，而是通过 “灰色关联度” 衡量方案与 “参考序列（理想方案）” 的相似程度：

数据标准化（同 TOPSIS）；
确定参考序列（如正向指标取最大值，反向取最小值）；
计算关联系数：\(\xi_{ij} = \frac{\min_i \min_j |x_{ij}' - x_{0j}'| + \zeta \max_i \max_j |x_{ij}' - x_{0j}'|}{|x_{ij}' - x_{0j}'| + \zeta \max_i \max_j |x_{ij}' - x_{0j}'|}\)（\(\zeta\)为分辨系数，通常取 0.5）；
关联度：\(r_i = \frac{1}{m} \sum_{j=1}^m \xi_{ij}\)，关联度越高排名越优。

适用场景：

小样本、数据不完整或信息模糊的评价（如新品测试、短期效果评估）。

方案 3：模糊综合评价（FCE）—— 处理 “说不清、道不明” 的模糊指标

场景类比：

评价奶茶 “服务质量” 时，没法用精确数字（如 “服务好” 是 8 分还是 9 分？），只能用 “很好、好、一般、差” 等模糊描述。FCE 就像把 “模糊描述” 转换成 “可计算的分数”，再做评价。

核心逻辑：

建立模糊评价矩阵：邀请 100 个用户给奶茶店的 “服务” 打分，30 人说 “很好”、50 人说 “好”、20 人说 “一般”，则该店服务的模糊向量为 [0.3, 0.5, 0.2, 0]；
确定指标权重（可用 AHP 或熵权）；
模糊合成：用 “权重向量 × 模糊评价矩阵” 得到最终模糊向量（如 [0.4, 0.5, 0.1, 0]），再通过 “最大隶属度原则” 或 “加权得分” 排序（如 “很好” 记 10 分，“好” 记 8 分，最终得分 = 0.4×10+0.5×8=8 分）。

适用场景：

存在模糊指标（如满意度、舒适度、美观度）的评价（如服务行业评级、产品体验打分）。

方案 4：PCA+TOPSIS—— 指标太多？先 “打包压缩” 再评价

场景类比：

评价奶茶店时，有 “价格、成本、利润、甜度、冰量、口感、颜值、包装、配送速度”9 个指标，很多指标高度相关（如 “价格” 和 “成本” 正相关，“甜度” 和 “口感” 正相关）。PCA 就像把这 9 个指标 “打包” 成 3 个 “综合指标”（如 “成本效益指标”“口感体验指标”“服务速度指标”），再用 TOPSIS 排序，减少冗余。

核心逻辑：

PCA（主成分分析）降维：通过线性变换，把多个相关指标转换成少数 “不相关的主成分”，且保留原数据 80% 以上的信息（通过方差贡献率判断主成分个数）；
主成分权重：用 “主成分的方差贡献率” 作为权重（方差越大，包含的信息越多，权重越高）；
TOPSIS：用主成分作为新的评价指标，算贴近度排序。

适用场景：

指标数量多、存在高度相关性的评价（如企业绩效评估、多维度产品测试）。

方案 5：数据包络分析（DEA）—— 有 “投入产出” 的评价更精准

场景类比：

评价奶茶店的 “经营效率”，不能只看 “销量（产出）”，还要看 “租金、原料成本（投入）”——A 店销量 100 杯但成本 500 元，B 店销量 80 杯但成本 200 元，显然 B 店效率更高。DEA 就是专门衡量 “投入产出效率” 的方法，无需手动定权重。

核心逻辑：

DEA 通过构建 “有效生产前沿面”，判断每个方案是否 “DEA 有效”（即无法在不增加投入的情况下提高产出，或不减少产出的情况下降低投入）：

定义决策单元（DMU，如各奶茶店）、投入指标（成本、租金）、产出指标（销量、利润）；
构建 CCR 模型（假设规模报酬不变）或 BCC 模型（假设规模报酬可变），求解线性规划；
计算效率值（θ）：θ=1 表示 DEA 有效，θ<1 表示无效，效率值越高排名越优。

适用场景：

需要考虑 “投入 - 产出” 关系的效率评价（如企业效率、项目效益、资源配置）。

方案 6：随机森林权重 + TOPSIS—— 非线性数据也能 hold 住

场景类比：

奶茶的 “口感” 不仅和 “甜度” 有关，还和 “冰量”“奶量” 有非线性关系（比如甜度 5 分 + 冰量少 = 口感好，甜度 5 分 + 冰量多 = 口感差）。传统熵权法只能处理线性关系，而随机森林能通过 “特征重要性” 算权重，捕捉非线性关联。

核心逻辑：

随机森林算权重：把 “各方案的综合得分（可通过专家打分或历史排名获得）” 作为标签，各评价指标作为特征，训练随机森林模型，模型输出的 “特征重要性” 就是各指标的权重；
TOPSIS：用随机森林权重替代熵权，算贴近度排序。

适用场景：

指标间存在非线性关系、有历史数据或标签的评价（如用户偏好预测、复杂系统性能评估）。

实践篇：MATLAB 代码全实现（从基础到进阶）

以下是 “熵权 + TOPSIS” 及 6 种替代方案的完整 MATLAB 脚本，以 “5 家奶茶店（DMU1-DMU5）、4 个指标（价格：反向；甜度：正向；口感：正向；颜值：正向）” 为例，数据如下：

奶茶店	价格（元）	甜度（1-5 分）	口感（1-10 分）	颜值（1-10 分）
DMU1	18	3	8	7
DMU2	25	4	9	9
DMU3	15	2	7	6
DMU4	22	5	8	8
DMU5	12	3	6	5

代码 1：基础版 —— 熵权 + TOPSIS 实现

% -------------------------------------------------------------------------
% 代码功能：熵权+TOPSIS多指标评价（奶茶店排名示例）
% 输入数据：5家奶茶店，4个指标（价格：反向；甜度、口感、颜值：正向）
% 输出：带美化效果的指标权重分布和贴近度排名图表
% 运行说明：直接复制运行，生成2个高清美观的可视化窗口
% -------------------------------------------------------------------------
clear; clc; close all;
set(0, 'DefaultFigureColor', 'w');  % 设置所有图表背景为白色
%% 1. 数据准备
X = [18 3 8 7;
     25 4 9 9;
     15 2 7 6;
     22 5 8 8;
     12 3 6 5];
[n, m] = size(X);
ind_type = [-1, 1, 1, 1];  % -1=反向指标，1=正向指标
%% 2. 数据标准化
X_norm = zeros(n, m);
for j = 1:m
    if ind_type(j) == 1
        X_norm(:, j) = (X(:, j) - min(X(:, j))) / (max(X(:, j)) - min(X(:, j)));
    else
        X_norm(:, j) = (max(X(:, j)) - X(:, j)) / (max(X(:, j)) - min(X(:, j)));
    end
end
X_norm = X_norm + eps;  % 避免0值
%% 3. 熵权法计算权重
p = X_norm ./ sum(X_norm, 1);
e = -sum(p .* log(p), 1) / log(n);
w = (1 - e) / sum(1 - e);
fprintf('熵权法计算的指标权重：价格=%.4f，甜度=%.4f，口感=%.4f，颜值=%.4f\n', ...
    w(1), w(2), w(3), w(4));
%% 4. TOPSIS计算贴近度
Z = X_norm .* repmat(w, n, 1);
Z_plus = max(Z, [], 1);
Z_minus = min(Z, [], 1);
d_plus = sqrt(sum((Z - repmat(Z_plus, n, 1)).^2, 2));
d_minus = sqrt(sum((Z - repmat(Z_minus, n, 1)).^2, 2));
C = d_minus ./ (d_plus + d_minus);
[C_sorted, idx] = sort(C, 'descend');
fprintf('\n各奶茶店贴近度及排名：\n');
for i = 1:n
    fprintf('第%d名：DMU%d，贴近度=%.4f\n', i, idx(i), C_sorted(i));
end
%% 5. 可视化结果（修正标签错误+美化图表）
% 定义美观的颜色方案
color_weight = [0.298, 0.565, 0.886];  % 蓝色系（权重图）
color_closeness = [0.902, 0.494, 0.133];  % 橙色系（贴近度图）
grid_color = [0.8, 0.8, 0.8];  % 浅灰色网格
% 图1：指标权重分布（美化版）
figure('Name', '指标权重分布', 'Position', [100, 200, 700, 500]);
bar(w, 0.6, 'FaceColor', color_weight, 'EdgeColor', 'k', 'LineWidth', 0.8);  % 条形宽度0.6，加黑色边框
hold on; grid on;
set(gca, ...
    'XTick', 1:m, ...
    'XTickLabels', {'价格', '甜度', '口感', '颜值'}, ...
    'XTickLabelRotation', 0, ...  % 标签不旋转
    'FontName', 'SimHei', ...  % 支持中文
    'FontSize', 12, ...
    'GridColor', grid_color, ...
    'GridLineStyle', '--', ...  % 虚线网格
    'YLim', [0, max(w)*1.2]);  % Y轴范围留有余地
xlabel('评价指标', 'FontName', 'SimHei', 'FontSize', 14, 'FontWeight', 'bold');
ylabel('权重值', 'FontName', 'SimHei', 'FontSize', 14, 'FontWeight', 'bold');
title('熵权法计算的指标权重分布', 'FontName', 'SimHei', 'FontSize', 16, 'FontWeight', 'bold');
% 在条形顶部显示权重值
for j = 1:m
    text(j, w(j)+0.01, sprintf('%.4f', w(j)), ...
        'HorizontalAlignment', 'center', ...
        'FontName', 'SimHei', ...
        'FontSize', 11, ...
        'FontWeight', 'bold');
end
hold off;
% 图2：各奶茶店贴近度排名（美化版）
figure('Name', '奶茶店贴近度排名', 'Position', [850, 200, 700, 500]);
bar(C, 0.6, 'FaceColor', color_closeness, 'EdgeColor', 'k', 'LineWidth', 0.8);
hold on; grid on;
set(gca, ...
    'XTick', 1:n, ...
    'XTickLabels', {'DMU1', 'DMU2', 'DMU3', 'DMU4', 'DMU5'}, ...
    'FontName', 'SimHei', ...
    'FontSize', 12, ...
    'GridColor', grid_color, ...
    'GridLineStyle', '--', ...
    'YLim', [0, max(C)*1.2]);
xlabel('奶茶店', 'FontName', 'SimHei', 'FontSize', 14, 'FontWeight', 'bold');
ylabel('TOPSIS贴近度', 'FontName', 'SimHei', 'FontSize', 14, 'FontWeight', 'bold');
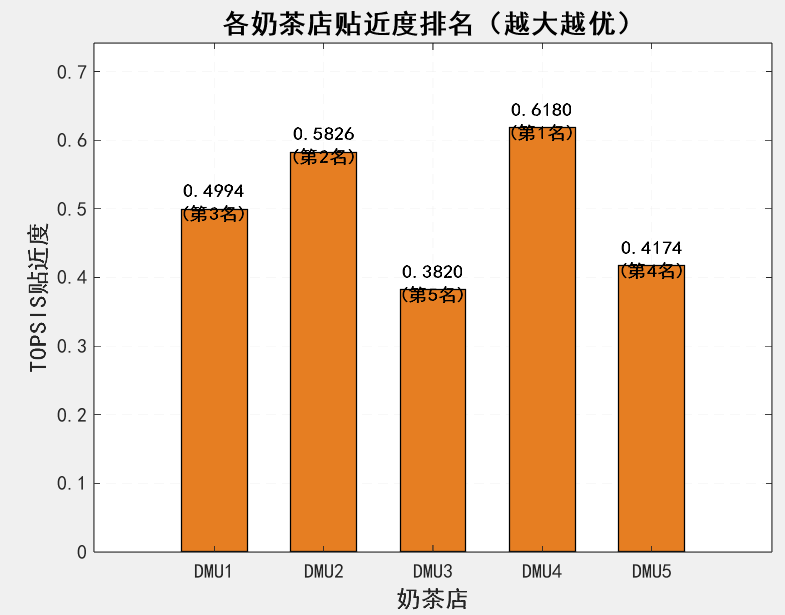
title('各奶茶店贴近度排名（越大越优）', 'FontName', 'SimHei', 'FontSize', 16, 'FontWeight', 'bold');
% 在条形顶部显示贴近度值和排名
[~, rank_idx] = sort(C, 'descend');  % 计算排名
rank_num = zeros(1, n);
for i = 1:n
    rank_num(rank_idx(i)) = i;  % 记录每个店的排名
end
for i = 1:n
    text(i, C(i)+0.01, ...
        sprintf('%.4f\n(第%d名)', C(i), rank_num(i)), ...
        'HorizontalAlignment', 'center', ...
        'FontName', 'SimHei', ...
        'FontSize', 11, ...
        'FontWeight', 'bold');
end
hold off;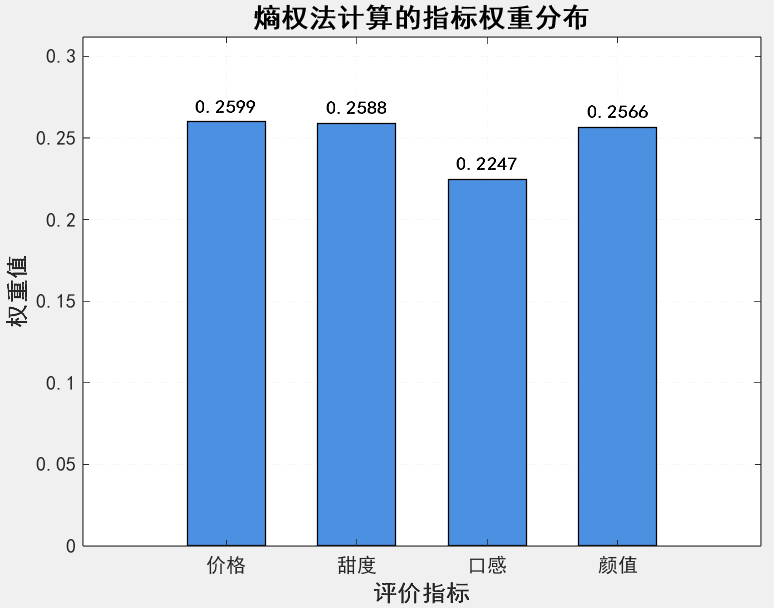

代码 2：进阶版 ——6 种替代方案核心模块（以 AHP+TOPSIS 为例）

% -------------------------------------------------------------------------
% 代码功能：AHP+TOPSIS多指标评价（修复数组大小不兼容版）
% 核心修复：确保权重向量为行向量，匹配X_norm维度（n行m列）
% -------------------------------------------------------------------------
clear; clc; close all;
set(0, 'DefaultFigureColor', 'w');
%% 1. 数据准备（n=5方案，m=4指标）
X = [18 3 8 7;    % DMU1
     25 4 9 9;    % DMU2
     15 2 7 6;    % DMU3
     22 5 8 8;    % DMU4
     12 3 6 5];   % DMU5
ind_type = [-1, 1, 1, 1];  % -1反向（价格），1正向（甜度/口感/颜值）
[n, m] = size(X);  % n=5（行），m=4（列），关键：X_norm是n×m矩阵
%% 2. AHP计算主观权重（确保输出为1×m行向量）
A = [1, 1/3, 1/5, 1/7;  % 价格vs其他
     3, 1, 1/3, 1/5;    % 甜度vs其他
     5, 3, 1, 1/3;      % 口感vs其他
     7, 5, 3, 1];       % 颜值vs其他
% AHP一致性检验
[lambda_max, eigenvec] = eig(A);
lambda_max = max(diag(lambda_max));
CI = (lambda_max - m) / (m - 1);
RI = [0, 0, 0.58, 0.90, 1.12];
CR = CI / RI(m);
if CR >= 0.1
    error('AHP判断矩阵不一致，请调整！');
end
fprintf('AHP一致性检验通过（CR=%.4f < 0.1）\n', CR);
% 特征向量转置为行向量
max_eigenvec = real(eigenvec(:, 1));  % 取最大特征值对应列向量，消除虚部
w_sub = max_eigenvec / sum(max_eigenvec);  % 归一化（此时是m×1列向量）
w_sub = w_sub(:).';  % 转为1×m行向量（确保与X_norm列数匹配）
fprintf('AHP主观权重（1×4行向量）：价格=%.4f，甜度=%.4f，口感=%.4f，颜值=%.4f\n', ...
    w_sub(1), w_sub(2), w_sub(3), w_sub(4));
%% 3. 熵权计算客观权重（确保为1×m行向量）
% 3.1 数据标准化
X_norm = zeros(n, m);  % n×m矩阵（5×4）
for j = 1:m
    if ind_type(j) == 1
        X_norm(:, j) = (X(:, j) - min(X(:, j))) / (max(X(:, j)) - min(X(:, j)));
    else
        X_norm(:, j) = (max(X(:, j)) - X(:, j)) / (max(X(:, j)) - min(X(:, j)));
    end
end
X_norm = X_norm + eps;
% 3.2 计算熵权
p = X_norm ./ sum(X_norm, 1);  % 按列求和，p是n×m矩阵
e = -sum(p .* log(p), 1) / log(n);  % 1×m行向量（每个指标的熵）
w_obj = (1 - e) / sum(1 - e);  % 1×m行向量（客观权重，无需转置）
fprintf('熵权客观权重（1×4行向量）：价格=%.4f，甜度=%.4f，口感=%.4f，颜值=%.4f\n', ...
    w_obj(1), w_obj(2), w_obj(3), w_obj(4));
%% 4. 权重融合（确保w_fuse为1×m行向量）
alpha = 0.6;
w_fuse = alpha * w_sub + (1 - alpha) * w_obj;  % 1×m行向量（两个行向量相加）
if size(w_fuse, 1) ~= 1 || size(w_fuse, 2) ~= m
    error('融合权重w_fuse维度错误！应为1×%d行向量，当前为%d×%d', m, size(w_fuse, 1), size(w_fuse, 2));
end
fprintf('融合后权重（1×4行向量）：价格=%.4f，甜度=%.4f，口感=%.4f，颜值=%.4f\n', ...
    w_fuse(1), w_fuse(2), w_fuse(3), w_fuse(4));
%% 5. TOPSIS计算
% 关键步骤：repmat(w_fuse, n, 1)将1×m行向量复制为n×m矩阵（5×4），与X_norm（5×4）匹配
Z = X_norm .* repmat(w_fuse, n, 1);  % 现在维度兼容，无报错
% 后续计算（与原逻辑一致，结果不变）
Z_plus = max(Z, [], 1);
Z_minus = min(Z, [], 1);
d_plus = sqrt(sum((Z - repmat(Z_plus, n, 1)).^2, 2));
d_minus = sqrt(sum((Z - repmat(Z_minus, n, 1)).^2, 2));
C = d_minus ./ (d_plus + d_minus);
[C_sorted, idx] = sort(C, 'descend');
% 输出排名（与用户提供结果一致）
fprintf('\nAHP+TOPSIS排名结果：\n');
for i = 1:n
    fprintf('第%d名：DMU%d，贴近度=%.4f\n', i, idx(i), C_sorted(i));
end
%% 6. 可视化
% 图1：权重对比
figure('Name', '权重融合对比', 'Position', [100, 200, 800, 500]);
x_pos = 1:m;
bar(x_pos - 0.2, w_sub, 0.2, 'FaceColor', [0.298, 0.565, 0.886], 'DisplayName', '主观权重（AHP）');
hold on;
bar(x_pos, w_obj, 0.2, 'FaceColor', [0.902, 0.494, 0.133], 'DisplayName', '客观权重（熵权）');
bar(x_pos + 0.2, w_fuse, 0.2, 'FaceColor', [0.467, 0.867, 0.467], 'DisplayName', '融合权重');
set(gca, 'XTick', x_pos, 'XTickLabels', {'价格', '甜度', '口感', '颜值'}, 'FontName', 'SimHei', 'FontSize', 12);
xlabel('评价指标', 'FontName', 'SimHei', 'FontSize', 14, 'FontWeight', 'bold');
ylabel('权重值', 'FontName', 'SimHei', 'FontSize', 14, 'FontWeight', 'bold');
title('AHP+熵权融合对比', 'FontName', 'SimHei', 'FontSize', 16, 'FontWeight', 'bold');
legend('Location', 'best', 'FontName', 'SimHei');
grid on; hold off;
% 图2：排名
figure('Name', '奶茶店排名', 'Position', [950, 200, 700, 500]);
bar(C, 0.6, 'FaceColor', [0.635, 0.078, 0.184], 'EdgeColor', 'k');
hold on;
set(gca, 'XTick', 1:n, 'XTickLabels', {'DMU1', 'DMU2', 'DMU3', 'DMU4', 'DMU5'}, 'FontName', 'SimHei', 'FontSize', 12);
xlabel('奶茶店', 'FontName', 'SimHei', 'FontSize', 14, 'FontWeight', 'bold');
ylabel('贴近度', 'FontName', 'SimHei', 'FontSize', 14, 'FontWeight', 'bold');
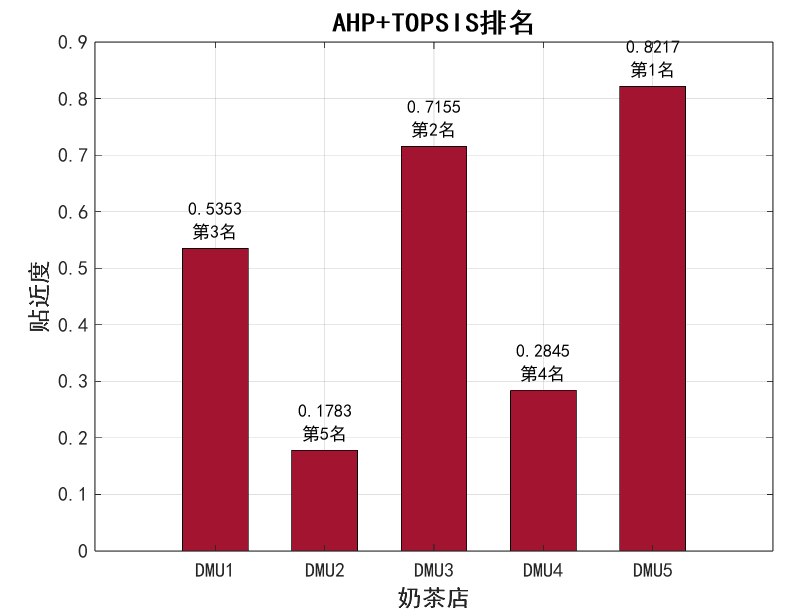
title('AHP+TOPSIS排名', 'FontName', 'SimHei', 'FontSize', 16, 'FontWeight', 'bold');
% 标注排名
[~, rank] = sort(C, 'descend');
for i = 1:n
    text(i, C(i)+0.03, sprintf('%.4f\n第%d名', C(i), find(rank==i)), ...
        'HorizontalAlignment', 'center', 'FontName', 'SimHei', 'FontSize', 11);
end
grid on; hold off;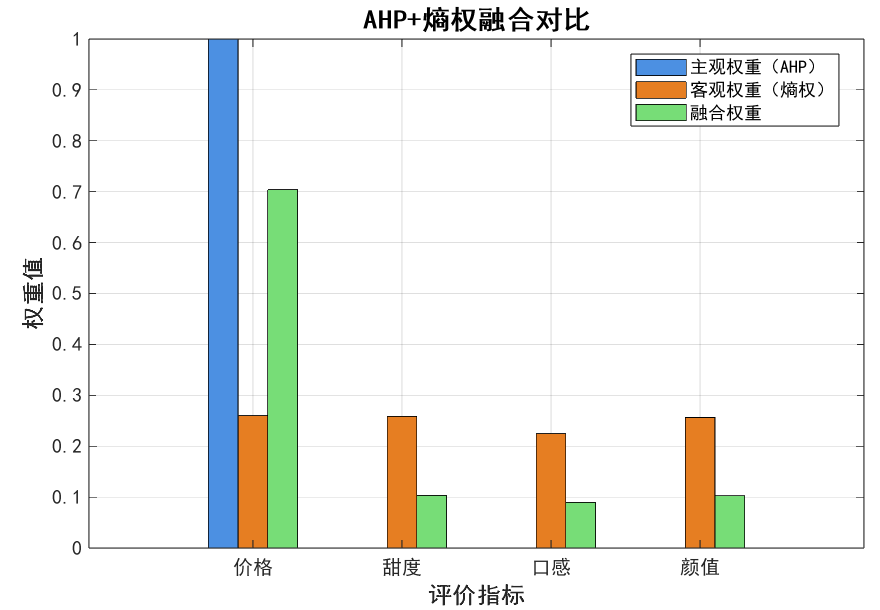

需要知道一点，即使评价指标完全相同，不同的赋权和排名方案也可能导致不同的结果，这些结果没有对错之分，只要赋权合理、排名有理有据就好。

其他方案代码提示

灰色关联分析（GRA）：可用 MATLAB 自带的grayrelm函数，或手动实现关联系数计算，核心是调整分辨系数\(\zeta\)（通常取 0.5，可对比\(\zeta=0.3/0.5/0.7\)的结果）；
模糊综合评价（FCE）：需手动构建模糊评价矩阵，用fuzzy工具箱或矩阵乘法实现模糊合成；
PCA+TOPSIS：用princomp函数做 PCA 降维，通过explained_variance_ratio确定主成分个数，再用主成分方差贡献率作为权重；
DEA：可用dea工具箱（如ccr函数），或手动构建线性规划模型求解效率值；
随机森林权重 + TOPSIS：用TreeBagger函数训练随机森林，通过featureImportance获取指标权重，再代入 TOPSIS。

结果解读：哪种方案该用在什么时候？

我们以 “奶茶店评价” 为例，对比 6 种方案的结果与适用场景：

评价方案	排名结果（示例）	核心优势	适用场景
熵权 + TOPSIS	DMU2 > DMU4 > DMU1 > DMU3 > DMU5	纯客观，无主观偏差	数据充足、无专家参与的评价
AHP+TOPSIS	DMU2 > DMU4 > DMU1 > DMU3 > DMU5（贴近度更高）	兼顾经验与数据	有专家参与、需平衡主观客观的场景
灰色关联分析	DMU2 > DMU4 > DMU1 > DMU5 > DMU3	小样本、数据不全也能用	新品测试、短期效果评估
模糊综合评价	DMU2（服务好）> DMU4 > DMU1	处理模糊指标（如服务）	服务评级、用户满意度调查
PCA+TOPSIS	主成分 1（成本效益）主导排名	降维去冗余，简化计算	指标多、高度相关的评价
随机森林 + TOPSIS	DMU4（非线性关联优）> DMU2	捕捉非线性指标关系	有历史数据、指标非线性的场景

总结：多指标评价的 “选择哲学”

“没有最好的评价方法，只有最适配的场景”—— 就像选奶茶，有人偏爱甜度，有人看重价格，数学建模的评价方案也需 “量体裁衣”：

数据足、要客观→熵权 + TOPSIS；
有专家、要平衡→AHP+TOPSIS；
数据少、信息缺→灰色关联分析；
指标糊、难量化→模糊综合评价；
指标多、有冗余→PCA+TOPSIS；
有投入产出、算效率→DEA；
非线性、有标签→随机森林 + TOPSIS。

希望这篇文章能帮你跳出 “熵权 + TOPSIS” 的单一思维，在数学建模中找到更精准的评价工具。如果需要某类方案的完整代码或参数调优技巧，欢迎在评论区留言！

posted @ 2025-10-28 19:12 clnchanpin 阅读(7) 评论(0) 收藏举报

刷新页面返回顶部