【关于封装的那些事】 缺失封装 【关于封装的那些事】 泄露的封装 【关于封装的那些事】 不充分的封装 【图解数据结构】二叉查找树 【图解数据结构】 二叉树遍历
【关于封装的那些事】 缺失封装

缺失封装
没有将实现变化封装在抽象和层次结构中时,将导致这种坏味。
表现形式通常如下:
- 客户程序与其需要的服务变种紧密耦合,每当需要支持新变种或修改既有变种时,都将影响客户程序。
- 每当需要在层次结构中支持新变种时,都添加了大量不必要的类,这增加了设计的复杂度。
为什么不能缺失封装?
开闭原则(OCP)指出,类型应对扩展开放,对修改关闭。也就是说应该通过扩展(而不是修改)来改变类型的行为。没有在类型或层次结构中封装实现变化时,便违反了OCP。
缺失封装潜在的原因
未意识到关注点会不断变化
没有预测到关注点可能发生变化,进而没有在设计中正确封装这些关注点。
混合关注点
将彼此独立的各个关注点聚合在一个层次结构中,而不是分开时,如果关注点发生变化,可能导致类的数量呈爆炸式增长。
幼稚的设计决策
采用过于简单的方法,如为每种变化组合创建一个类时,可能导致设计无谓的复杂。
示例分析一
假设有一个Entryption类,它需要使用加密算法对数据进行加密。可供选择的加密算法有很多,包括DES(数据加密标准)、AES(高级加密标准)、TDES(三重数据加密标准)等。Entryption类使用DES算法对数据进行加密。
public class Encryption
{
/// <summary>
/// 使用DES算法进行加密
/// </summary>
public void Encrypt()
{
// 使用DES算法进行加密
}
}假设出现了新需求,要求使用AES算法对数据进行加密。
最差的方案出现了:
public class Encryption
{
/// <summary>
/// 使用DES算法进行加密
/// </summary>
public void EncryptUsingDES()
{
// 使用DES算法进行加密
}
/// <summary>
/// 使用AES算法进行加密
/// </summary>
public void EncryptUsingAES()
{
// 使用AES算法进行加密
}
}这种方案有很多不尽如人意的地方:
- Encryption类变得更大、更难以维护,因为它实现了多种加密算法,但是每次只使用一种。
- 难以添加新算法以及修改既有算法,因为加密算法是Encryption类不可分割的部分。
- 加密算法向Encryption类提供服务,但是与Encryption类紧紧耦合在一起,无法在其它地方重用。
不满意就重构,首先使用继承进行重构,会有2种方案可以选择:
选择1:
让Encryption类根据需求继承AESEncryptionAlgorithm或DESEncryptionAlgorithm类,并提供方法Encrypt()。这种方案带来的问题是Encryption类在编译阶段就将关联到特定的加密算法,更严重的是类之间的关系并不是is-a关系。
/// <summary>
/// AES算法加密类
/// </summary>
public class AESEncryptionAlgorithm
{
/// <summary>
/// 使用AES算法进行加密
/// </summary>
public void EncryptUsingAES()
{
// 使用AES算法进行加密
}
}
/// <summary>
/// DES算法加密类
/// </summary>
public class DESEncryptionAlgorithm
{
/// <summary>
/// 使用DES算法进行加密
/// </summary>
public void EncryptUsingDES()
{
// 使用DES算法进行加密
}
}
public class Encryption: AESEncryptionAlgorithm
{
/// <summary>
/// 使用算法进行加密
/// </summary>
public void Encrypt()
{
EncryptUsingAES();
}
}选择2:
创建子类AESEncryption和DESEncryption,它们都扩展了Encryption类,并分别包含加密算法AES和DES的实现。客户程序可创建Encryption的引用,这些引用指向特定子类的对象。通过添加新的子类,很容易支持新的加密算法。但是这种方案的问题是AESEncryption和DESEncryption将继承Encryption类的其它方法,降低了加密算法的可重用性。
public abstract class Encryption
{
/// <summary>
/// 使用算法进行加密
/// </summary>
public abstract void Encrypt();
}
/// <summary>
/// AES算法加密类
/// </summary>
public class AESEncryption : Encryption
{
/// <summary>
/// 使用 AES算法进行加密
/// </summary>
public override void Encrypt()
{
// 使用 AES算法进行加密
}
}
/// <summary>
/// DES算法加密类
/// </summary>
public class DESEncryption : Encryption
{
/// <summary>
/// 使用 DES算法进行加密
/// </summary>
public override void Encrypt()
{
// 使用 DES算法进行加密
}
}最佳的选择是使用策略模式:
- 可在运行阶段给Encryption对象配置特定的加密算法
- 可在其它地方重用层次结构EncryptionAlgorithm中定义的算法
- 很容易根据需要支持新的算法
/// <summary>
/// 算法加密接口
/// </summary>
public interface EncryptionAlgorithm
{
void Encrypt();
}
/// <summary>
/// DES算法加密类
/// </summary>
public class DESEncryptionAlgorithm : EncryptionAlgorithm
{
public void Encrypt()
{
//使用 DES算法进行加密
}
}
/// <summary>
/// AES算法加密类
/// </summary>
public class AESEncryptionAlgorithm : EncryptionAlgorithm
{
public void Encrypt()
{
//使用 AES算法进行加密
}
}
public class Encryption
{
private EncryptionAlgorithm algo;
public Encryption(EncryptionAlgorithm algo)
{
this.algo = algo;
}
/// <summary>
/// 使用算法进行加密
/// </summary>
public void Encrypt()
{
algo.Encrypt();
}
}示例分析二
支持使用不同算法(DES和AES)对各种内容(Image和Text)进行加密的设计。
最简单最直观的的设计:

在这个设计中,有两个变化点:支持的内容类型和加密算法类型。对于这两个变化点的每种可能组合,都使用了一个类来表示。这样会有一个严重的问题:假设现在要求支持新加密算法TDES和新内容类型Data,类的数量呈爆炸性增长。因为变化点混在了一起,没有分别进行封装。

使用桥接模式进行封装:

使用桥接模式,分别封装这两个关注点的变化。现在要引入新内容类型Data和新加密算法TDES,只需要添加两个新类。既解决了类数量呈爆炸增长的问题,又增加了根为接口EncryptionAlgorithm层次结构中的加密算法的可重用性。
总结
-
不相关的关注点混在一起,抽象将变得难以重用。
-
对业务中可能的变化点,要给予扩展点,保证开闭原则(OCP),对扩展开放,对修改关闭。
【关于封装的那些事】 泄露的封装

泄露的封装
抽象通过公有接口(方法)暴露或泄露实现细节时,将导致这种坏味。需要注意的是,即使抽象不存在“不充分的封装”坏味,其公有接口也有可能泄露实现细节。
为什么不能泄露封装?
为实现有效封装,必须将抽象的接口(即抽象的内容)和实现(即抽象的方式)分离。为遵循隐藏原则,必须对客户程序隐藏抽象的实现方面。
如果通过公有接口暴露了实现细节(违反了隐藏原则)可能会造成:
- 对实现进行修改时,可能会影响客户程序
- 暴露的实现细节可能会让客户程序能够通过公有接口访问内部数据结构,进而有意或无意地损坏抽象的内部状态。
泄露的封装的潜在原因
不知道该隐藏哪些东西
开发人员通常会在无意之间泄露实现细节。
使用细粒度接口
类的公有接口直接提供了细粒度的方法,这些细粒度的方法通常会向客户程序暴露不必要的实现细节。更好的做法是在类的公有接口提供粗粒度的方法,在粗粒度方法内部使用细粒度的私有方法。
示例分析一
我们用程序来维护一个待办事项列表。在ToDoList类中,公有方法GetListEntries()返回对象存储的待办事项列表。
public class ToDoList
{
private List<string> listEntries = new List<string>();
public List<string> GetListEntries()
{
return listEntries;
}
public void AddListEntry(string entry)
{
}
}问题出在方法的返回类型上,它暴露了一个内部细节,ToDoList内部使用List来存储待办事项列表。
现在问题来了,如果待办事项列表程序主要执行插入和删除操作,那么选择使用List没啥问题;但是后来发现查找频率比修改频率高,那么使用HashTable可能更合适。然而GetListEntries()的返回类型是List,如果修改这个方法的返回类型,可能破坏依赖于这个方法的客户程序。如果要支持未来数据结构的变更,方法返回类型可以使用IEnumerable(C#中的集合类型都实现的接口类型),这样可以做到在不改变方法签名的条件下(里氏替换原则),替换存储待办事项列表的数据结构。
重构后的代码实现:
使用List数据结构:
public class ToDoList
{
private List<string> listEntries = new List<string>();
public IEnumerable GetListEntries()
{
return listEntries;
}
public void AddListEntry(string entry)
{
}
}使用Hashtable数据结构:
public class ToDoList
{
private Hashtable listEntries = new Hashtable();
public IEnumerable GetListEntries()
{
return listEntries;
}
public void AddListEntry(string entry)
{
}
}方法GetListEntries()存在另一个严重的问题是,它返回一个指向内部数据结构的引用,通过这个引用,客户程序可以绕过AddListEntry()方法直接修改数据结构。当然如果使用IEnumerable这个问题也就迎刃而解了,因为IEnumerable接口没有相应的针对于某一种数据集合的操作。
public interface IEnumerable
{
//
// 摘要:
// 返回循环访问集合的枚举数。
//
// 返回结果:
// 一个可用于循环访问集合的 System.Collections.IEnumerator 对象。
[DispId(-4)]
IEnumerator GetEnumerator();
}示例分析二
假设显式图像包含4个步骤,这些步骤必须按照特定顺序执行,图形才可以正常显式。
现在在Image类中提供4个公有方法Load(),Process(),Validate(),Show()供客户程序使用,但是这样有一个很麻烦的问题是写客户程序的开发人员不一定会按照正确顺序调用方法使用(永远不要给客户选择的权利)。而且客户程序只是想要显式图像,我们为什么要向它们暴露4个内部步骤呢?这就是泄露的封装的潜在原因——使用细粒度接口。
public class Image
{
public void Load()
{
}
public void Process()
{
}
public void Validate()
{
}
public void Show()
{
}
}要解决这个问题,可以让Image类只向客户程序暴露一个方法Display(),然后在这个方法内部按照特定顺序调用4个步骤方法。
public class Image
{
private void Load()
{
}
private void Process()
{
}
private void Validate()
{
}
private void Show()
{
}
public void Display()
{
Load();
Process();
Validate();
Show();
}
}总结
- 抽象通过公有接口暴露或泄露了实现细节时,客户程序可能直接依赖于实现细节吗,这种直接依赖性使得难以在不破坏既有客户代码的情况下对设计进行修改或扩展。
- 抽象泄露了内部数据结构时,抽象的完整性遭到了破坏。增加了代码运行阶段发生问题的可能性。
参考:《软件设计重构》
【关于封装的那些事】 不充分的封装
封装原则倡导通过隐藏抽象的实现细节和隐藏变化等来实现关注点分离和信息隐藏。
封装原则的实现手法

- 隐藏实现细节
抽象向客户端程序只暴露其提供的功能,而将实现方式隐藏起来。实现方式(即实现细节)包含抽象的内部表示(如抽象使用的数据成员和数据结构)以及有关方法是如何实现的细节(如方法使用的算法)。
- 隐藏变化
隐藏类型或实现结构的实现变化。通过隐藏变化,更容易在不给客户端程序带来太大影响的情况下修改抽象的实现。
违反封装原则导致的坏味

我们这篇博客主要讲解分析不充分的封装坏味,对于其它封装坏味将在后面的博客讲解分析。
不充分的封装
对于抽象的一个或多个成员,声明的访问权限超过了实际需求时,将导致这种坏味。这种坏味的极端表现形式是,存在一些用全局变量、全局数据结构等表示的全局状态,整个软件系统的所有抽象都可以访问它们。
为什么要有充分的封装?
封装的主要意图是将接口和实现分离,以便能够几乎独立地修改它们。这种关注点分离让客户端程序只依赖于抽象的接口,从而能够对它们隐藏实现细节。如果暴露了实现细节,将导致抽象和客户端紧密耦合。这是不可取的,每当修改抽象的实现细节时,都将影响客户端程序。提供超过需要的访问权限可能向客户端程序暴露实现细节,这违反了“隐藏原则”。
不充分的封装的潜在原因
为方便测试
为了方便测试,开发人员常常将抽象的私有方法改成公有的。由于私有方法涉及抽象的实现细节,将其改为公有将破坏抽象的封装。
我们都知道代码的可测试性是衡量代码质量的一个重要指标。如果编写的代码无法进行单元测试,代码的质量就无法得到保证。在有些情况下,代码无法编写测试是可以进行代码修改的,我们称之为重构。但是因为访问权限修改代码不在这些情况下,这样做反而会破坏代码的封装。可以借助反射实现低访问权限成员的测试。
在面向对象编程中采用过程型思维
以全局变量的方式暴露多个抽象需要使用的数据,从而导致这种坏味。
示例分析
/// <summary>
/// 消息发布类
/// </summary>
public class Publisher
{
/// <summary>
/// 频道号 范围1-100
/// </summary>
public int channel;
/// <summary>
/// 创建一个特定频道的发布者对象
/// </summary>
/// <param name="channel">频道号 范围1-100</param>
public Publisher(int channel)
{
this.channel = channel;
}
public vois Publish(string message)
{
//向频道channel发布消息message
}
}上面代码示例就是不充分的封装的典型,频道号变量channel被设置为public是不合适的,因为创建消息发布对象时就已经指定发布的频道号,channel被设置为public,频道号在客户端使用的时候就可以随意的被访问修改,这样客户端就会了解消息发布类的内部实现,造成了直接依赖,违反了“高内聚,低耦合”原则。这样每当修改内部实现时都会对客户端造成影响。更重要的一点是频道号变量channel是有范围限定的(1-100),客户端使用的时候随意的修改channel,可能会造成channel越界的错误。所以正确的做法是将channel变量设置为私有的,并且为其提供合适的存取器方法。
重构后的代码实现:
/// <summary>
/// 消息发布类
/// </summary>
public class Publisher
{
/// <summary>
/// 频道号 范围1-100
/// </summary>
private int channel;
/// <summary>
/// channel赋值,支持范围限定
/// </summary>
/// <param name="channel">频道号 范围1-100</param>
public void SetChannel(int channel)
{
if(channel < 1 || channel > 100)
{
throw new ArgumentOutOfRangeException("超出频道号 范围1-100");
}
this.channel = channel;
}
/// <summary>
/// 创建一个特定频道的发布者对象
/// </summary>
/// <param name="channel">频道号 范围1-100</param>
public Publisher(int channel)
{
SetChannel(channel);
}
public vois Publish(string message)
{
//向频道channel发布消息message
}
}还有一种极端表现形式:全局变量。对于全局变量,存在两种不同的情形。
- 将一个或多个成员设置为全局可见的,但是只有少量类会访问它们。
- 将一个或多个成员设置为全局可见的,有大量的类会访问它们。
对于第一种情形,要进行重构,可以通过参数传递必要的变量。
对于第二种情形,要进行重构,可以根据其承担的责任创建合适的抽象,并在这些抽象中封装原来的全局变量,这样客户端就会使用这些抽象,而不是直接使用全局变量。
总结
-
存在不充分的封装坏味时,会使代码的可重用性大打折扣,因为客户程序直接依赖大家都可以访问的状态,导致难以在其它地方重用客户程序。
-
抽象允许直接访问其数据成员时,确保数据和整个抽象完整性的职责由抽象转移到了各个客户程序。增加了代码运行阶段发生问题的可能性。
-
相对于使用存取器方法控制对变量访问修改带来的好处,使用存取器方法带来的性能开销可以忽略不计。
【图解数据结构】二叉查找树
目录
二叉查找树定义
每棵子树头节点的值都比各自左子树上所有节点值要大,也都比各自右子树上所有节点值要小。
二叉查找树的中序遍历序列一定是从小到大排列的。
二叉查找树节点定义
/// <summary>
/// 二叉查找树节点
/// </summary>
public class Node
{
/// <summary>
/// 节点值
/// </summary>
public int Data { get; set; }
/// <summary>
/// 左子节点
/// </summary>
public Node Left { get; set; }
/// <summary>
/// 右子节点
/// </summary>
public Node Right { get; set; }
/// <summary>
/// 打印节点值
/// </summary>
public void DisplayNode()
{
Console.Write(Data + " ");
}
}插入节点
二叉查找树的插入节点操作相对比较简单,只需要找到要插入节点的位置放置即可。
插入节点的整体流程:
- 把父节点设置为当前节点,即根节点。
如果新节点内的数据值小于当前节点内的数据值,那么把当前节点设置为当前节点的左子节点。如果新节点内的数据值大于当前节点内的数据值,那么就跳到步骤 4。
如果当前节点的左子节点的数值为空(null),就把新节点插入在这里并且退出循环。否则,跳到 while 循环的下一次循环操作中。
- 把当前节点设置为当前节点的右子节点。
如果当前节点的右子节点的数值为空(null),就把新节点插入在这里并且退出循环。否则,跳到 while 循环的下一次循环操作中。
代码实现:
public class BinarySearchTree
{
public Node root;
public BinarySearchTree()
{
root = null;
}
/// <summary>
/// 二叉查找树插入结点
/// </summary>
/// <param name="i"></param>
public void Insert(int i)
{
Node newNode = new Node
{
Data = i
};
if (root == null)
{
root = newNode;
}
else
{
Node current = root;
Node parent;
while (true)
{
parent = current;
if (i < current.Data)
{
current = current.Left;
if (current == null)
{
parent.Left = newNode;
break;
}
}
else
{
current = current.Right;
if (current == null)
{
parent.Right = newNode;
break;
}
}
}
}
}
}因为二叉查找树的中序遍历序列一定是由小到大排列的,所以我们可以通过中序遍历测试二叉查找树的插入操作。关于二叉树遍历操作可以移步我的上一篇博客【图解数据结构】 二叉树遍历。
中序遍历代码实现:
/// <summary>
/// 二叉查找树中序遍历
/// </summary>
/// <param name="node"></param>
public void InOrder(Node node)
{
if (node != null)
{
InOrder(node.Left);
node.DisplayNode();
InOrder(node.Right);
}
}测试代码:
class BinarySearchTreeTest
{
static void Main(string[] args)
{
BinarySearchTree bst = new BinarySearchTree();
bst.Insert(23);
bst.Insert(45);
bst.Insert(16);
bst.Insert(37);
bst.Insert(3);
bst.Insert(99);
bst.Insert(22);
Console.WriteLine("中序遍历: ");
bst.InOrder(bst.root);
Console.ReadKey();
}
}测试结果:
上面的测试代码形成了一棵这样的二叉查找树:

查找节点
对于 二叉查找树(BST) 有三件最容易做的事情:查找一个特殊数值,找到最小值,以及找到最大值。
查找最小值
根据二叉查找树的性质,二叉查找树的最小值一定是在左子树的最左侧子节点。
所以实现很简单,就是从根结点出发找出二叉查找树左子树的最左侧子节点。
代码实现:
/// <summary>
/// 查找二叉查找树最小值
/// </summary>
/// <returns></returns>
public int FindMin()
{
Node current = root;
while (current.Left != null)
{
current = current.Left;
}
return current.Data;
}查找最大值
根据二叉查找树的性质,二叉查找树的最大值一定是在右子树的最右侧子节点。
所以实现很简单,就是从根结点出发找出二叉查找树右子树的最右侧子节点。
代码实现:
/// <summary>
/// 查找二叉查找树最大值
/// </summary>
/// <returns></returns>
public int FindMax()
{
Node current = root;
while (current.Right != null)
{
current = current.Right;
}
return current.Data;
}查找特定值
根据二叉查找树的性质,从根结点开始,比较特定值和根结点值的大小。如果比根结点值大,则说明特定值在根结点右子树上,继续在右子节点执行此操作;如果比根结点值小,则说明特定值在根结点左子树上,继续在左子节点执行此操作。如果到执行完成都没有找到和特定值相等的节点值,那么二叉查找树中没有包含此特定值的节点。
代码实现:
/// <summary>
/// 查找二叉查找树特定值节点
/// </summary>
/// <param name="key">特定值</param>
/// <returns></returns>
public Node Find(int key)
{
Node current = root;
while (current.Data != key)
{
if (key < current.Data)
{
current = current.Left;
}
if (key > current.Data)
{
current = current.Right;
}
// 如果已到达 BST 的末尾
if (current == null)
{
return null;
}
}
return current;
}删除节点
相对于前面的操作,二叉查找树的删除节点操作就显得要复杂一些了,因为删除节点会有破坏 BST 正确
层次顺序的风险。
我们都知道在二叉查找树中的结点可分为:没有子节点的节点,带有一个子节点的节点 ,带有两个子节点的节点 。那么可以将二叉查找树的删除节点操作简单拆分一下,以便于我们的理解。如下图:

删除叶子节点
删除叶子节点是最简单的事情。 唯一要做的就是把目标节点的父节点的一个子节点设置为空(null)。
查看这个节点的左子节点和右子节点是否为空(null),都为空(null)说明为叶子节点。
然后检测这个节点是否是根节点。如果是,就把它设置为空(null)。
否则,如果isLeftChild 为true,把父节点的左子节点设置为空(null);如果isLeftChild 为false,把父节点的右子节点设置为空(null)。
代码实现:
//要删除的结点是叶子结点的处理
if (current.Left == null && current.Right == null)
{
if (current == root)
root = null;
else if (isLeftChild)
parent.Left = null;
else
{
parent.Right = null;
}
}删除带有一个子节点的节点
当要删除的节点有一个子节点的时候,需要检查四个条件:
- 这个节点的子节点可能是左子节点;
- 这个节点的子节点可能是右子节点;
- 要删除的这个节点可能是左子节点;
- 要删除的这个节点可能是右子节点。

代码实现:
//要删除的结点是带有一个子节点的节点的处理
//首先判断子结点是左子节点还是右子节点,然后再判断当前节点是左子节点还是右子节点
else if (current.Right == null)
if (current == root)
root = current.Left;
else if (isLeftChild)
parent.Left = current.Left;
else
parent.Right = current.Left;
else if (current.Left == null)
if (current == root)
root = current.Right;
else if (isLeftChild)
parent.Left = current.Right;
else
parent.Right = current.Right;删除带有两个子节点的节点
如果要删除标记为 52 的节点,需要重构这棵树。这里不能用起始节点为 54 的子树来替换它,因为 54 已经有一个左子节点了。这个问题的答案是把中序后继节点移动到要删除节点的位置上。 当然还要区分后继节点本身是否有子节点。


这里我们需要了解一下后继节点的定义。
一个节点的后继节点是指,这个节点在中序遍历序列中的下一个节点。相应的,前驱节点是指这个节点在中序遍历序列中的上一个节点。
举个例子,下图中的二叉树中序遍历序列为: DBEAFCG,则A的后继节点为F,A的前驱节点为E。

了解了这些,删除带有两个子节点的节点的操作就可以转化为寻找要删除节点的后继节点并且把要删除节点的右子树赋给后继结点的右子节点,这里需要注意的是如果后继节点本身有子节点,则需要将后继节点的子结点赋给后继节点父节点的左子节点。
先上获取后继结点的代码,然后举个例子说明:
/// <summary>
/// 获取后继结点
/// </summary>
/// <param name="delNode">要删除的结点</param>
/// <returns></returns>
public Node GetSuccessor(Node delNode)
{
//后继节点的父节点
Node successorParent = delNode;
//后继节点
Node successor = delNode.Right;
Node current = delNode.Right.Left;
while (current != null)
{
successorParent = successor;
successor = current;
current = current.Left;
}
//如果后继结点不是要删除结点的右子结点,
//则要将后继节点的子结点赋给后继节点父节点的左节点
//删除结点的右子结点赋给后继结点作为 后继结点的后继结点
if (successor != delNode.Right)
{
successorParent.Left = successor.Right;
successor.Right = delNode.Right;
}
return successor;
}删除带有两个子节点的节点的代码实现:
//要删除的结点是带有两个子节点的节点的处理
else
{
Node successor = GetSuccessor(current);
if (current == root)
root = successor;
else if (isLeftChild)
parent.Left = successor;
else
parent.Right = successor;
//因为后继结点是要删除结点右子树的最左侧结点
//所以后继结点的左子树肯定是要删除结点左子树
successor.Left = current.Left;
}我们观察到删除节点的后继节点一定是删除节点右子树的最左侧节点。这里有3种情况:
后继节点是删除节点的子节点

删除节点37,后继节点40是删除节点37的子节点。delNode是结点37,successor是节点40,delNode.Right是节点40,successor == delNode.Right,后继节点为删除节点的子节点,这种情况是最简单的。
后继节点不是删除节点的子节点

后继节点38是删除节点37右子树的最左侧节点。delNode是节点37,successor是节点38,successorParent 是节点40,delNode.Right 是节点40。successor != delNode.Right,所以要将 successorParent.Left = successor.Right;successor.Right = delNode.Right;。因为successor.Right==null,所以successorParent.Left = null。successor.Right = delNode.Right,节点40成为了节点38的右子节点。因为删除节点的后继节点一定是删除节点右子树的最左侧节点,所以后继节点肯定没有左子节点。删除节点被删除后,后继结点会补到删除节点的位置。successor.Left = current.Left;,也就是删除节点的左子节点变成了后继节点的左子节点。
完成删除节点后的搜索二叉树变为:

后继节点不是删除节点的子节点且有子节点

这种情况和上一种情况相似,唯一的区别是后继节点有子节点(注意肯定是右子节点)。也就是successorParent.Left = successor.Right;,后继节点的右子节点变成后继结点父节点的左子节点。因为successor.Right是节点39,所以节点40的左子节点变成了节点39。其它操作和上一种情况完全相同。
完成删除节点后的搜索二叉树变为:

删除节点操作的整体流程:
- 把后继节点的右子节点赋值为后继节点的父节点的左子节点。
- 把要删除节点的右子节点赋值为后继节点的右子节点。
- 从父节点的右子节点中移除当前节点,并且把它指向后继节点。
- 从当前节点中移除当前节点的左子节点,并且把它指向后继节点的左子节点。
综合以上删除节点的三种情况,删除节点操作的完整代码如下:
/// <summary>
/// 二叉查找树删除节点
/// </summary>
/// <param name="key"></param>
/// <returns></returns>
public bool Delete(int key)
{
//要删除的当前结点
Node current = root;
//当前结点的父结点
Node parent = root;
//当前结点是否是左子树
bool isLeftChild = true;
//先通过二分查找找出要删除的结点
while (current.Data != key)
{
parent = current;
if (key < current.Data)
{
isLeftChild = true;
current = current.Left;
}
else
{
isLeftChild = false;
current = current.Right;
}
if (current == null)
return false;
}
//要删除的结点是叶子结点的处理
if (current.Left == null && current.Right == null)
{
if (current == root)
root = null;
else if (isLeftChild)
parent.Left = null;
else
{
parent.Right = null;
}
}
//要删除的结点是带有一个子节点的节点的处理
else if (current.Right == null)
if (current == root)
root = current.Left;
else if (isLeftChild)
parent.Left = current.Left;
else
parent.Right = current.Left;
else if (current.Left == null)
if (current == root)
root = current.Right;
else if (isLeftChild)
parent.Left = current.Right;
else
parent.Right = current.Right;
//要删除的结点是带有两个子节点的节点的处理
else
{
Node successor = GetSuccessor(current);
if (current == root)
root = successor;
else if (isLeftChild)
parent.Left = successor;
else
parent.Right = successor;
//因为后继结点是要删除结点右子树的最左侧结点
//所以后继结点的左子树肯定是要删除结点左子树
successor.Left = current.Left;
}
return true;
}
/// <summary>
/// 获取后继结点
/// </summary>
/// <param name="delNode">要删除的结点</param>
/// <returns></returns>
public Node GetSuccessor(Node delNode)
{
//后继节点的父节点
Node successorParent = delNode;
//后继节点
Node successor = delNode.Right;
Node current = delNode.Right.Left;
while (current != null)
{
successorParent = successor;
successor = current;
current = current.Left;
}
//如果后继结点不是要删除结点的右子结点,
//则要将后继节点的子结点赋给后继节点父节点的左节点
//删除结点的右子结点赋给后继结点作为 后继结点的后继结点
if (successor != delNode.Right)
{
successorParent.Left = successor.Right;
successor.Right = delNode.Right;
}
return successor;
}删除节点测试
我们还是使用中序遍历进行测试,首先构造二叉查找树:
static void Main(string[] args)
{
BinarySearchTree bst = new BinarySearchTree();
bst.Insert(23);
bst.Insert(45);
bst.Insert(16);
bst.Insert(37);
bst.Insert(3);
bst.Insert(99);
bst.Insert(22);
bst.Insert(40);
bst.Insert(35);
bst.Insert(38);
bst.Insert(44);
bst.Insert(39);
} 构造出的二叉查找树:

测试分三种情况:
测试删除叶子节点
删除叶子节点39
Console.Write("删除节点前: ");
bst.InOrder(bst.root);
bst.Delete(39);
Console.Write("删除节点后: ");
bst.InOrder(bst.root);测试结果:
测试删除带有一个子节点的节点
删除带有一个子节点的节点38
Console.Write("删除节点前: ");
bst.InOrder(bst.root);
bst.Delete(38);
Console.Write("删除节点后: ");
bst.InOrder(bst.root);测试结果:
测试删除带有两个子节点的节点
删除带有两个子节点的节点37
Console.Write("删除节点前: ");
bst.InOrder(bst.root);
bst.Delete(37);
Console.Write("删除节点后: ");
bst.InOrder(bst.root);测试结果:
参考:
《数据结构与算法 C#语言描述》
《大话数据结构》
《数据结构与算法分析 C语言描述》
五一大家都出去happy了,为什么我还要自己在家撸代码,是因为爱吗?是因为责任吗?都不是。是因为我的心里只有学习(其实是因为穷)。哈哈,提前祝大家五一快乐,吃好玩好!
【图解数据结构】 二叉树遍历
目录
扯一扯

昨天在看《极客时间》严嘉伟老师的《如何做出好的职业选择——认识你的职业锚》专题直播时,严老师讲到了关于选择的一些问题,我认为其中的一些点讲的非常好,总结一下分享给大家。
人为什么难做选择?
选择意味着放弃
你选择一方,也就意味着放弃了另一方。摆在你面前的选择项越接近,你的选择就会越困难,因为放弃其中任何一个选择项都不容易。如果摆在你面前的选择项对比明显,那么选择起来就会轻松许多,大家几乎都会毫不犹豫的选择“好”的选择项,放弃掉“差”的选择项。
选择永远都不是完美的
选择永远都不可能十全十美,只可能满足尽量多的侧重点。选择的时候想满足越多的侧重点,可能就会越难做出选择。所以在选择上不要过于追求完美。
警惕逃避性选择——不知道自己要去哪儿,还要选择离开。
有一种选择是对现状不满,想逃离这种现状,但是却不知道去哪里。举个例子,可能目前的公司有各种问题,比如开发流程不规范等,如果因为这些问题离开,可能就会从一个坑跳到另外一个更大的坑。当决定离开的时候,一定是自己有明确的目标,很清楚自己想要什么。
二叉树遍历原理
二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。
为什么研究二叉树的遍历?
因为计算机只会处理线性序列,而我们研究遍历,就是把树中的结点变成某种意义的线性序列,这给程序的实现带来了好处。
二叉树的创建
遍历二叉树之前,首先我们要有一个二叉树。要创建一个如下图的二叉树,就要先进行二叉树的扩展,也就是将二叉树每个结点的空指针引出一个虚结点,其值为一个特定值,比如'#'。处理后的二叉树称为原二叉树的扩展二叉树。扩展二叉树的每个遍历序列可以确定一个一颗二叉树,我们采用前序遍历创建二叉树。前序遍历序列:124##5##36##7##。


定义二叉链表结点:
/// <summary>
/// 二叉链表结点类
/// </summary>
/// <typeparam name="T"></typeparam>
public class TreeNode<T>
{
/// <summary>
/// 数据域
/// </summary>
public T Data { get; set; }
/// <summary>
/// 左孩子
/// </summary>
public TreeNode<T> LChild { get; set; }
/// <summary>
/// 右孩子
/// </summary>
public TreeNode<T> RChild { get; set; }
public TreeNode(T val, TreeNode<T> lp, TreeNode<T> rp)
{
Data = val;
LChild = lp;
RChild = rp;
}
public TreeNode(TreeNode<T> lp, TreeNode<T> rp)
{
Data = default(T);
LChild = lp;
RChild = rp;
}
public TreeNode(T val)
{
Data = val;
LChild = null;
RChild = null;
}
public TreeNode()
{
Data = default(T);
LChild = null;
RChild = null;
}
}先序递归创建二叉树:
/// <summary>
/// 先序创建二叉树
/// </summary>
/// <param name="node"></param>
public static void CreateTree(TreeNode<char> node)
{
node.Data = Console.ReadKey().KeyChar;
if (node.Data == '#')
{
return;
}
node.LChild = new TreeNode<char>();
CreateTree(node.LChild);
if (node.LChild.Data == '#')
{
node.LChild = null;
}
node.RChild = new TreeNode<char>();
CreateTree(node.RChild);
if (node.RChild.Data == '#')
{
node.RChild = null;
}
}二叉树遍历方法


前序遍历

递归方式实现前序遍历
具体过程:
- 先访问根节点
- 再序遍历左子树
- 最后序遍历右子树
代码实现:
public static void PreOrderRecur(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
Console.Write(treeNode.Data);
PreOrderRecur(treeNode.LChild);
PreOrderRecur(treeNode.RChild);
}非递归方式实现前序遍历
具体过程:
- 首先申请一个新的栈,记为stack;
- 将头结点head压入stack中;
- 每次从stack中弹出栈顶节点,记为cur,然后打印cur值,如果cur右孩子不为空,则将右孩子压入栈中;如果cur的左孩子不为空,将其压入stack中;
- 重复步骤3,直到stack为空.
代码实现:
public static void PreOrder(TreeNode<char> head)
{
if (head == null)
{
return;
}
Stack<TreeNode<char>> stack = new Stack<TreeNode<char>>();
stack.Push(head);
while (!(stack.Count == 0))
{
TreeNode<char> cur = stack.Pop();
Console.Write(cur.Data);
if (cur.RChild != null)
{
stack.Push(cur.RChild);
}
if (cur.LChild != null)
{
stack.Push(cur.LChild);
}
}
}过程模拟:
执行结果:
中序遍历

递归方式实现中序遍历
具体过程:
- 先中序遍历左子树
- 再访问根节点
- 最后中序遍历右子树
代码实现:
public static void InOrderRecur(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
InOrderRecur(treeNode.LChild);
Console.Write(treeNode.Data);
InOrderRecur(treeNode.RChild);
}非递归方式实现中序遍历
具体过程:
- 申请一个新栈,记为stack,申请一个变量cur,初始时令cur为头节点;
- 先把cur节点压入栈中,对以cur节点为头的整棵子树来说,依次把整棵树的左子树压入栈中,即不断令cur=cur.left,然后重复步骤2;
- 不断重复步骤2,直到发现cur为空,此时从stack中弹出一个节点记为node,打印node的值,并让cur = node.right,然后继续重复步骤2;
- 当stack为空并且cur为空时结束。
代码实现:
public static void InOrder(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
Stack<TreeNode<char>> stack = new Stack<TreeNode<char>>();
TreeNode<char> cur = treeNode;
while (!(stack.Count == 0) || cur != null)
{
while (cur != null)
{
stack.Push(cur);
cur = cur.LChild;
}
TreeNode<char> node = stack.Pop();
Console.WriteLine(node.Data);
cur = node.RChild;
}
}过程模拟:
执行结果:
后序遍历

递归方式实现后序遍历
- 先后序遍历左子树
- 再后序遍历右子树
- 最后访问根节点
代码实现:
public static void PosOrderRecur(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
PosOrderRecur(treeNode.LChild);
PosOrderRecur(treeNode.RChild);
Console.Write(treeNode.Data);
}非递归方式实现后序遍历一
具体过程:
使用两个栈实现
- 申请两个栈stack1,stack2,然后将头结点压入stack1中;
- 从stack1中弹出的节点记为cur,然后先把cur的左孩子压入stack1中,再把cur的右孩子压入stack1中;
- 在整个过程中,每一个从stack1中弹出的节点都放在第二个栈stack2中;
- 不断重复步骤2和步骤3,直到stack1为空,过程停止;
- 从stack2中依次弹出节点并打印,打印的顺序就是后序遍历的顺序;
代码实现:
public static void PosOrderOne(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
Stack<TreeNode<char>> stack1 = new Stack<TreeNode<char>>();
Stack<TreeNode<char>> stack2 = new Stack<TreeNode<char>>();
stack1.Push(treeNode);
TreeNode<char> cur = treeNode;
while (!(stack1.Count == 0))
{
cur = stack1.Pop();
if (cur.LChild != null)
{
stack1.Push(cur.LChild);
}
if (cur.RChild != null)
{
stack1.Push(cur.RChild);
}
stack2.Push(cur);
}
while (!(stack2.Count == 0))
{
TreeNode<char> node = stack2.Pop();
Console.WriteLine(node.Data); ;
}
}过程模拟:

执行结果:
非递归方式实现后序遍历二
具体过程:
使用一个栈实现
申请一个栈stack,将头节点压入stack,同时设置两个变量 h 和 c,在整个流程中,h代表最近一次弹出并打印的节点,c代表当前stack的栈顶节点,初始时令h为头节点,,c为null;
每次令c等于当前stack的栈顶节点,但是不从stack中弹出节点,此时分一下三种情况:
(1)如果c的左孩子不为空,并且h不等于c的左孩子,也不等于c的右孩子,则吧c的左孩子压入stack中
(2)如果情况1不成立,并且c的右孩子不为空,并且h不等于c的右孩子,则把c的右孩子压入stack中;
(3)如果情况1和2不成立,则从stack中弹出c并打印,然后令h等于c;
- 一直重复步骤2,直到stack为空.
代码实现:
public static void PosOrderTwo(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
Stack<TreeNode<char>> stack = new Stack<TreeNode<char>>();
stack.Push(treeNode);
TreeNode<char> h = treeNode;
TreeNode<char> c = null;
while (!(stack.Count == 0))
{
c = stack.Peek();
//c结点有左孩子 并且 左孩子没被遍历(输出)过 并且 右孩子没被遍历过
if (c.LChild != null && h != c.LChild && h != c.RChild)
stack.Push(c.LChild);
//c结点有右孩子 并且 右孩子没被遍历(输出)过
else if (c.RChild != null && h != c.RChild)
stack.Push(c.RChild);
//c结点没有孩子结点 或者孩子结点已经被遍历(输出)过
else
{
TreeNode<char> node = stack.Pop();
Console.WriteLine(node.Data);
h = c;
}
}
}过程模拟:
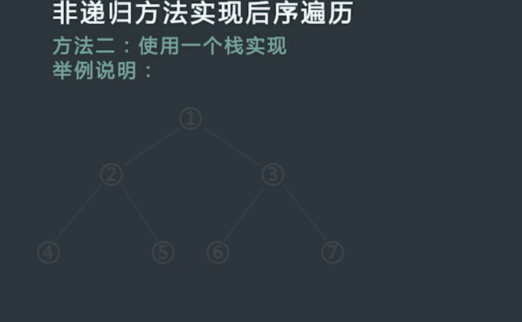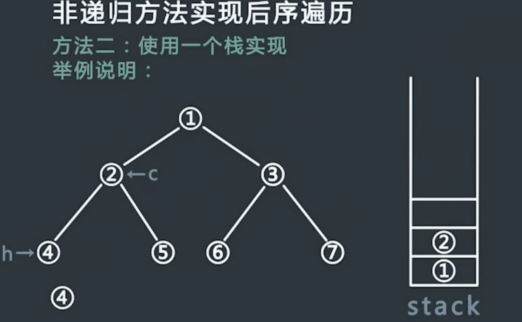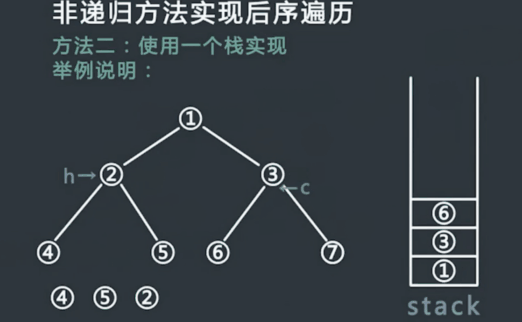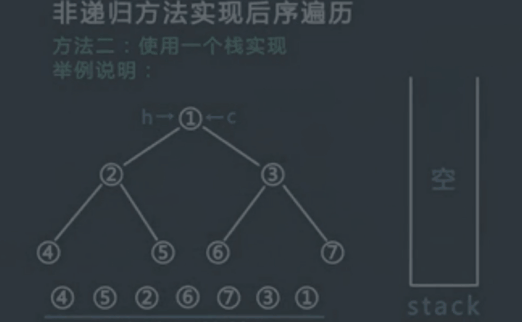
执行结果:
层序遍历

具体过程:
- 首先申请一个新的队列,记为queue;
- 将头结点head压入queue中;
- 每次从queue中出队,记为node,然后打印node值,如果node左孩子不为空,则将左孩子入队;如果node的右孩子不为空,则将右孩子入队;
- 重复步骤3,直到queue为空。
代码实现:
public static void LevelOrder(TreeNode<char> treeNode)
{
if(treeNode == null)
{
return;
}
Queue<TreeNode<char>> queue = new Queue<TreeNode<char>>();
queue.Enqueue(treeNode);
while (queue.Any())
{
TreeNode<char> node = queue.Dequeue();
Console.Write(node.Data);
if (node.Left != null)
{
queue.Enqueue(node.Left);
}
if (node.Right != null)
{
queue.Enqueue(node.Right);
}
}
}执行结果:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号