AtCoder Grand Contest 039
Preface
我发现我现在打AT真的是只会D-Before……
E,F都是抄曲明姐姐的,然后D还是几何画板猜结论做的(证明都是陈指导想的)
看来再这样下去就真的要退役了啊233
A - Connection and Disconnection
JB A题卡我好久(大雾)
我们考虑把一个串的答案先统计出来,填的时候显然尽量向后填。然后判断中间交的地方有哪些要修改
然后WA了,容易发现这样没有充分考虑两个串之间的影响,那么显然可以把两个串接在一起做再判断
然后还是WA了,我们发现只从前往后可能会考虑不充分,因此再尽量往前填一遍算答案即可
然后终于是过了
#include<cstdio>
#include<cstring>
#include<algorithm>
#define RI register int
#define CI const int&
using namespace std;
const int N=105;
int n,k; long long ans1,ans2; char s[N*3],t[N*3];
int main()
{
RI i; for (scanf("%s%d",s+1,&k),n=strlen(s+1),i=1;i<=n;++i)
s[i+n]=s[i+(n<<1)]=t[i]=t[i+n]=t[i+(n<<1)]=s[i];
if (k==1)
{
for (i=2;i<=n;++i) if (s[i]==s[i-1]) s[i]='%',++ans1;
} else
{
for (i=2;i<=(n<<1);++i) if (s[i]==s[i-1]) s[i]='%',++ans1; ans1*=(k>>1);
if (s[n<<1]==s[1]) ans1+=(k>>1)-1; if (k&1) for (i=(n<<1)+1;i<=3*n;++i)
if (s[i]==s[i-1]) s[i]='%',++ans1;
}
reverse(t+1,t+3*n+1);
if (k==1)
{
for (i=2;i<=n;++i) if (t[i]==t[i-1]) s[i]='%',++ans2;
} else
{
for (i=2;i<=(n<<1);++i) if (t[i]==t[i-1]) t[i]='%',++ans2; ans2*=(k>>1);
if (t[n<<1]==t[1]) ans2+=(k>>1)-1; if (k&1) for (i=(n<<1)+1;i<=3*n;++i)
if (t[i]==t[i-1]) t[i]='%',++ans2;
}
return printf("%lld",ans1<ans2?ans1:ans2),0;
}
B - Graph Partition
SB题,比A题好写到不知道那里去了
数据范围这么小我们为什么不直接暴力BFS呢?
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=205;
int n,q[N],d[N],col[N],ans; bool g[N][N];
inline char get_digit(void)
{
char ch; while (ch=getchar(),ch!='0'&&ch!='1'); return ch;
}
inline bool BFS(CI st)
{
RI H=0,T=1,i; for (q[1]=st,i=1;i<=n;++i) col[i]=-1,d[i]=1e9;
col[st]=0; d[st]=1; while (H<T)
{
int now=q[++H]; for (i=1;i<=n;++i) if (g[now][i])
{
if (!~col[i]) col[i]=col[now]^1,d[i]=d[now]+1,q[++T]=i;
else if (col[now]==col[i]) return 0; else d[i]=min(d[i],d[now]+1);
}
}
for (i=1;i<=n;++i) ans=max(ans,d[i]); return 1;
}
int main()
{
RI i,j; for (scanf("%d",&n),i=1;i<=n;++i)
for (j=1;j<=n;++j) g[i][j]=get_digit()-48;
for (i=1;i<=n;++i) if (!BFS(i)) return puts("-1"),0;
return printf("%d",ans),0;
}
C - Division by Two with Something
陈指导在证明D题结论的时候我莫名找出了这题的性质,然后就过了。。。
考虑我们统计出有多少种串在经过\(k\)次反向操作(就是把前面的数放到后面)后可以变回自己
为了方便统计,我们转化下问题:将一个串全部取反后接在原串后面,然后我们发现进行\(k\)次反向操作后能变回原串当且仅当这个串有一个长度为\(k\)的循环节
我们在挖掘一下性质就会发现\(\frac{2n}{k}\mod 2= 1\),因为若\(\frac{2n}{k}\mod 2= 0\)那么说明这个串的反串与原串相等
然后根据这一条我们容易推导出\(k\)必为偶数,然后我们考虑把\(k\)这个串从\(\frac{k}{2}\)处分开,它也是对称的,证明如下:
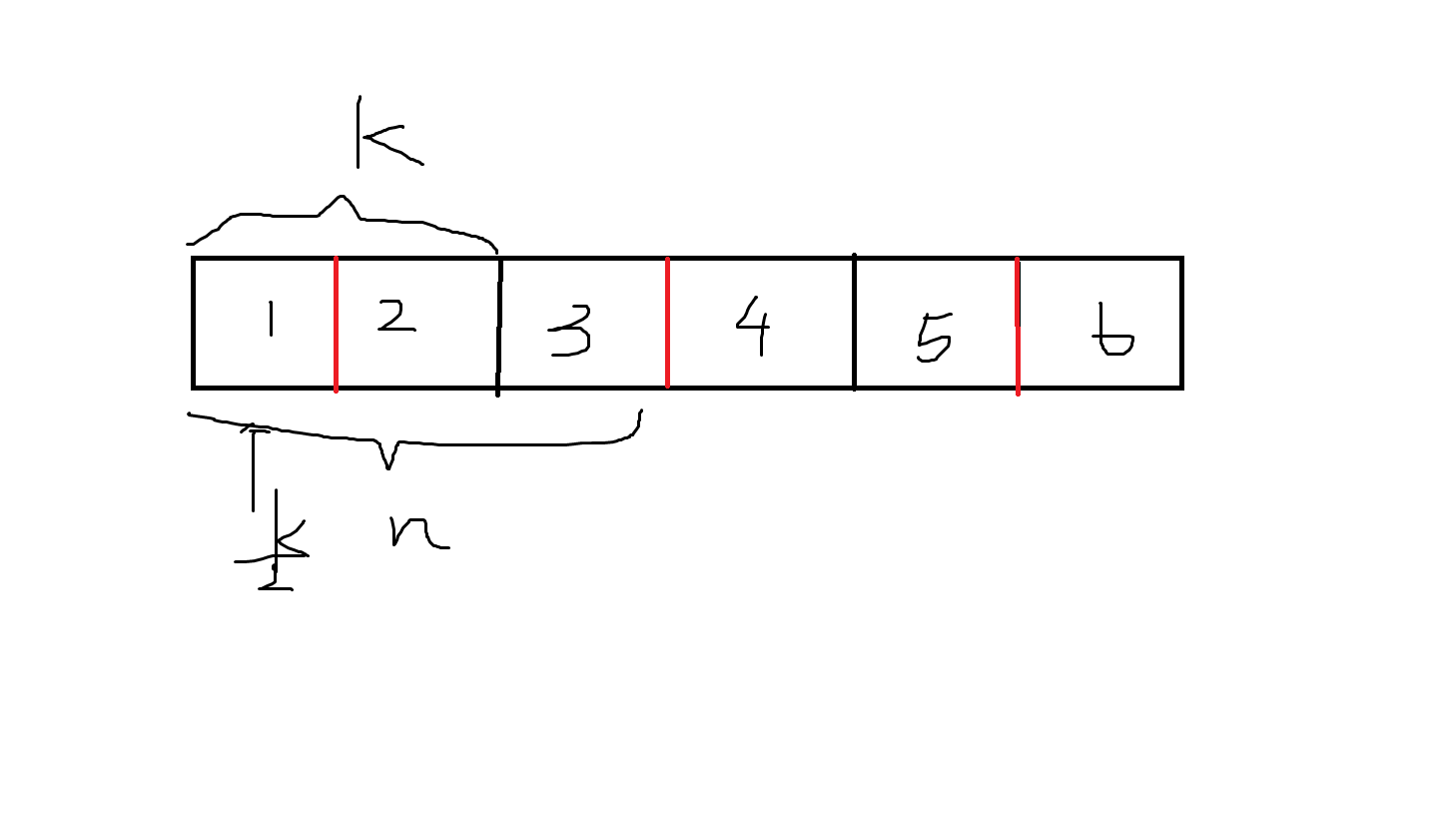
显然现在最中间的一段即\(3,4\)中间的\(\frac{k}{2}\)与\(n\)重合,由\(1=3=5;\ 2=4=6\)且\(3,4\)互反即可推出\(1,2;\ 3,4;\ 5,6\)互反
考虑有了这个性质之后我们可以干嘛,我们可以枚举\(k\),然后统计合法的\(\frac{k}{2}\)的串的个数
然后我们发现这个串只需要满足字典序小于原串即可,那么前\(\frac{k}{2}\)比原来小显然是合法的,那么我们只需要判断相等的时候是否合法即可,暴力特判一下
最后我们发现我们算出来的是以\(k\)为循环节而不是最小为\(k\),那我们只需要容斥一下即可
#include<cstdio>
#define RI register int
#define CI const int&
using namespace std;
const int N=400005,mod=998244353;
int n,ans,num[N],g[N],tot; char s[N],t[N];
inline void inc(int& x,CI y)
{
if ((x+=y)>=mod) x-=mod;
}
inline void dec(int& x,CI y)
{
if ((x-=y)<0) x+=mod;
}
int main()
{
RI i,j,k; for (scanf("%d%s",&n,s+1),k=1;k<=(n<<1);++k)
if ((n<<1)%k==0&&(((n<<1)/k)&1))
{
for (num[++tot]=k,i=1;i<=(k>>1);++i)
g[tot]=((g[tot]<<1)+s[i]-48)%mod,t[i]=s[i];
for (i=(k>>1)+1;i<=n;++i) t[i]=((t[i-(k>>1)]-48)^1)+48;
for (++g[tot],i=1;i<=n;++i) if (t[i]!=s[i])
{ g[tot]-=(t[i]>s[i]); break; }
}
for (i=1;i<tot;++i) for (j=i+1;j<=tot;++j)
if (num[j]%num[i]==0) dec(g[j],g[i]);
for (i=1;i<=tot;++i) inc(ans,1LL*num[i]*g[i]%mod);
return printf("%d",ans),0;
}
D - Incenters
为我的可怜的平面几何知识缅怀,我们先掏出几何画板画个图:
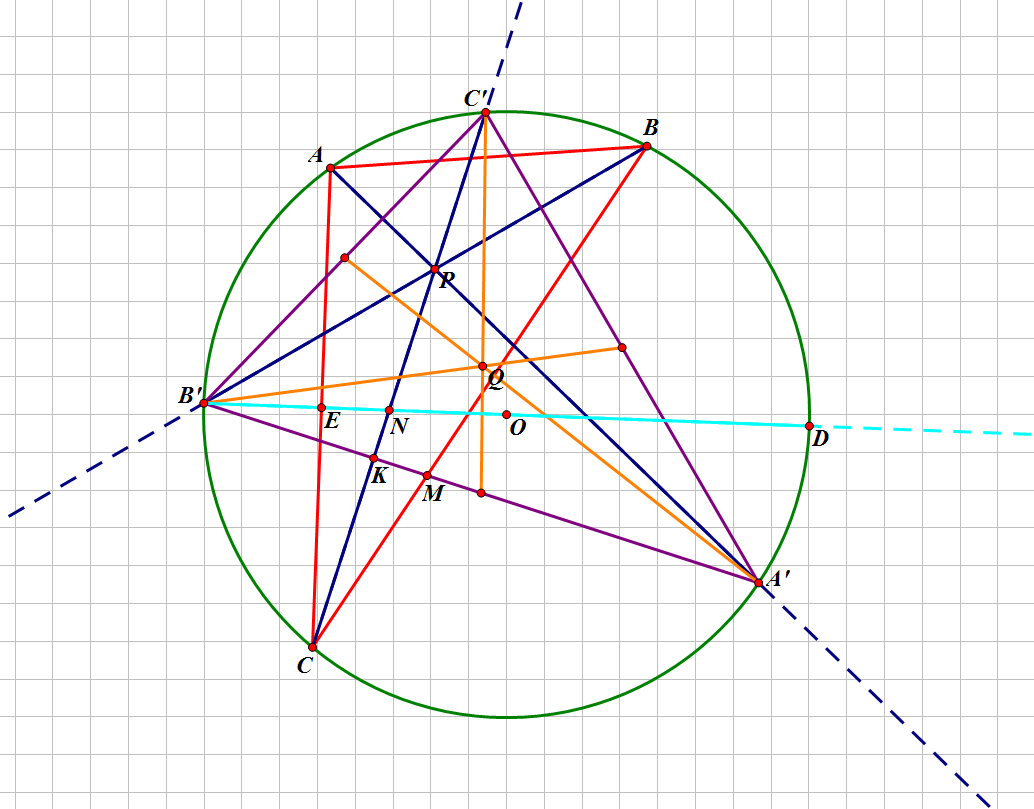
这里的\(A,B,C\)三点是我们选出来的,连接\(AB,AC,BC\)就可以得到如图所示的红色三角形
然后做出它的内心\(P\),三条蓝色的线就是角平分线,延长交于圆\(A',B',C'\),然后连接这三点就得到了紫色三角形
然后我们可以得到两个至关重要的结论(以下结论的证明请移步至陈指导的博客观看):
Ⅰ:点\(C'\)是弧\(AB\)的中点
Ⅱ:点\(P\)是\(\triangle A'B'C'\)的垂心
考虑垂心再怎么转化,我们发现\(\triangle A'B'C'\)的外心也出现了(原点\(O\)),那么容易联想到联系它们的欧拉线
我们做出\(\triangle A'B'C'\)的重心\(Q\),那么有\(O,Q,P\)三点共线且\(2|OQ|=|PQ|\)
那么我们发现现在我们经过一些列转化,把内心→垂心→重心,而重心非常适合期望的式子,因为它就是三角形三边坐标的平均值
考虑具体怎么计算,我们先\(n^2\)枚举一条边\(AB\),然后考虑另一个点\(C'\)的位置就确定了
而根据\(A,B\)之间的点数我们很容易确定\(C'\)在优弧和劣弧上的方案数,因此我们就可以把\(C'\)的贡献统计出来
然后由于期望的线性性,我们统计所有的这样的点之后三角形三点的贡献其实都得出来了
那么最后我们除去方案数,再乘上\(3\)就是答案了
#include<cstdio>
#include<cmath>
#define RI register int
#define CI const int&
using namespace std;
const int N=3005;
const double pi=acos(-1);
int n,l,t[N],cur; double ansx,ansy;
int main()
{
RI i,j; for (scanf("%d%d",&n,&l),i=1;i<=n;++i) scanf("%d",&t[i]);
for (i=1;i<n;++i) for (cur=0,j=i+1;j<=n;++j,++cur)
{
ansx+=1.0*(n-2-cur)*cos(pi*(t[i]+t[j])/l)/(n-2);
ansy+=1.0*(n-2-cur)*sin(pi*(t[i]+t[j])/l)/(n-2);
ansx-=1.0*cur*cos(pi*(t[i]+t[j])/l)/(n-2);
ansy-=1.0*cur*sin(pi*(t[i]+t[j])/l)/(n-2);
}
double ct=1.0*n*(n-1)/2.0; ansx/=ct; ansy/=ct;
return printf("%.16lf %.16lf",3.0*ansx,3.0*ansy),0;
}
E - Pairing Points
代码奇短的DP题,被打爆了。。。ORZ 曲明姐姐
首先我们考虑把环破开,比如我们枚举与\(1\)相连的那个点\(i\),然后我们发现现在我们要将\([2,i)\cup(i,2\times n]\)的点进行配对,考虑现在又哪些性质:
- \([2,i)\cup(i,2\times n]\)的点都未连边,且\([2,i)\)只会和\([2,i)\)的点连边,另一遍同理
- \(i\)已经向\([2,2\times n]\)外的一点连边
考虑到这样的状态很有代表性,因此我们可以把它定义成一个基本的状态
我们令\(f(l,r,m)\)表示\([l,r]\)中\(m\)向外连边的情况
考虑我们现在枚举一条边\(j\leftrightarrow k\),其中\(j\in [l,m),k\in (m,r]\),显然这条边横跨了整个区间,且与\(m\)向外连的边有交点
然后我们考虑\((j,m)\)之间的点,它们之间的边肯定要么与\(j\leftrightarrow k\)这条边相连,或者与\(m\)向外连的边相连,且中间一定有一个分界点\(p\),满足\((j,p]\)之间的边都与\(j\leftrightarrow k\)相交(以上强烈建议画图理解)
那么这时我们发现\([l,j)\cup (j,p]\)与\(m\)连出的边不再有任何关系,因此它就可以划分成一个子问题\(f(l,p,j)\)
同理我们在\((m,r]\)中可以找到一个点\(q\),然后划分出问题\(f(q,r,k)\)
同时\((p,m)\cup (m,q)\)之间的点还是以\(m\)连出去的边为横跨边,因此还可以划分出\(f(p+1,q-1,m)\)
综上所述这题就做完了,状态数是\(n^3\)的,转移是\(n^4\)的,因此复杂度为\(O(n^7)\),不过显然跑不满
#include<cstdio>
#include<cstring>
#define RI register int
#define CI const int&
using namespace std;
const int N=45;
int n; char g[N][N]; long long f[N][N][N],ans;
inline long long DP(CI l,CI r,CI m)
{
if (~f[l][r][m]) return f[l][r][m]; long long ret=0;
if (l==r) return 1; if (l==m||r==m) return 0;
for (RI j=l,k,p,q;j<m;++j) for (k=m+1;k<=r;++k)
if (g[j][k]=='1') for (p=j;p<m;++p) for (q=m+1;q<=k;++q)
ret+=DP(l,p,j)*DP(p+1,q-1,m)*DP(q,r,k); return f[l][r][m]=ret;
}
int main()
{
RI i; for (scanf("%d",&n),n<<=1,i=1;i<=n;++i) scanf("%s",g[i]+1);
for (memset(f,-1,sizeof(f)),i=2;i<=n;++i)
if (g[1][i]=='1') ans+=DP(2,n,i); return printf("%lld",ans),0;
}
F - Min Product Sum
究极玄学DP,ORZ 曲明姐姐
我们考虑原问题等价于对于一个矩阵\(B\),我们重新填一个矩阵\(A\)使得\(A_{i,j}\)小于\((i,j)\)这一行和这一列的最小值的方案数
然后再转化一步,相当于\(A\)中每行每列的最大值小于等于\(B\)中每行每列的最大值
那么最终答案就变成求这样的\(A,B\)的方案数
考虑记一个\(X_p\)表示\(A\)中第\(p\)行的最大值,\(Y_p\)表示\(B\)中第\(p\)列的最小值
然后设一个状态\(f_{i,j,k}\)表示已经考虑玩了所有的\(X_p\le k\)的\(i\)行,\(Y_p\le k\)的\(j\)列,此时的方案数,转移分在A和B中填写两步:
- 枚举\(X_p=k+1\)的行数,那么对于每一个这样的行,我们在矩阵\(B\)中已经考虑完\(Y_p\le k\)的那\(j\)列中显然可以任取\(\ge k+1\)的数,而且在矩阵\(A\)还未考虑的那\(m-j\)列中,显然可以任取\(\le k+1\)的数,但是得保证至少有一个\(k+1\)
- 枚举\(Y_p=k+1\)的列数,那么对于每一个这样的列,我们在矩阵\(B\)中已经考虑完\(X_p\le k\)的那\(i\)行中显然可以任取\(\ge k+1\)的数,且至少有一个\(k+1\)。而在矩阵\(A\)还未考虑的那\(n-i\)行中,显然可以任取\(\le k+1\)的数
那么我们在DP的状态中加一维\(0/1\)表示转移的两步,一定要从\(0\to 1\)再从\(1\to \text{下一个}0\)
那么此时我们会发现DP转移的系数不能直接计算,因此我们还要用DP预处理转移的系数
#include<cstdio>
#include<iostream>
#define RI int
#define CI const int&
using namespace std;
const int N=105;
int n,m,s,mod,ans,C[N][N],f[N][N][N][2],coef[N][N][N][2];
inline void inc(int& x,CI y)
{
if ((x+=y)>=mod) x-=mod;
}
inline int sum(CI x,CI y)
{
int t=x+y; return t>=mod?t-mod:t;
}
inline int sub(CI x,CI y)
{
int t=x-y; return t<0?t+mod:t;
}
inline int quick_pow(int x,int p=mod-2,int mul=1)
{
for (;p;p>>=1,x=1LL*x*x%mod) if (p&1) mul=1LL*mul*x%mod; return mul;
}
int main()
{
RI i,j,k,l; scanf("%d%d%d%d",&n,&m,&s,&mod);
for (C[0][0]=i=1;i<=max(n,m);++i) for (C[i][0]=j=1;j<=i;++j)
C[i][j]=sum(C[i-1][j],C[i-1][j-1]);
for (k=1;k<=s;++k) for (i=0;i<=m;++i)
{
int cur=1LL*quick_pow(s-k+1,i)*sub(quick_pow(k,m-i),quick_pow(k-1,m-i))%mod;
for (coef[k][i][0][0]=j=1;j<=n;++j) coef[k][i][j][0]=1LL*coef[k][i][j-1][0]*cur%mod;
}
//for (k=1;k<=s;++k) for (i=0;i<=m;++i) for (j=0;j<=n;++j)
//printf("%d ",coef[k][i][j][0]); putchar('\n');
for (k=1;k<=s;++k) for (i=0;i<=n;++i)
{
int cur=1LL*quick_pow(k,n-i)*sub(quick_pow(s-k+1,i),quick_pow(s-k,i))%mod;
for (coef[k][i][0][1]=j=1;j<=m;++j) coef[k][i][j][1]=1LL*coef[k][i][j-1][1]*cur%mod;
}
//for (k=1;k<=s;++k) for (i=0;i<=m;++i) for (j=0;j<=n;++j)
//printf("%d ",coef[k][i][j][1]); putchar('\n');
for (f[1][0][0][0]=k=1;k<=s;++k) for (i=0;i<=n;++i) for (j=0;j<=m;++j)
{
for (l=0;l<=n-i;++l)
inc(f[k][i+l][j][1],1LL*f[k][i][j][0]*C[n-i][l]%mod*coef[k][j][l][0]%mod);
for (l=0;l<=m-j;++l)
inc(f[k+1][i][j+l][0],1LL*f[k][i][j][1]*C[m-j][l]%mod*coef[k][i][l][1]%mod);
}
return printf("%d",f[s+1][n][m][0]),0;
}
Postscript
AGC真是越来越难打了,CSP前天天做这个搞得我自信心全无233……


 浙公网安备 33010602011771号
浙公网安备 33010602011771号