2 八大排序

排序稳定性：相等的两个元素，排序后的顺序和排序前保持一致即稳定。

排序算法性能度量：时间性能、辅助空间、算法复杂性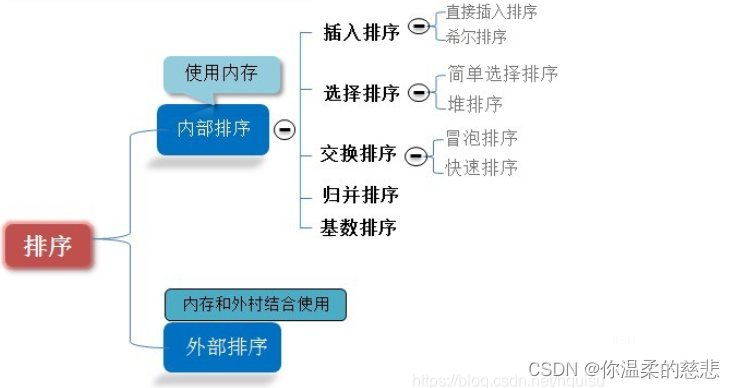

 

1.冒泡排序

基本思想：两两比较相邻记录的关键字，如果反序则交换，直到没有反序的记录。

public void bubbleSort(int[] elem) {
        for (int i = 1; i < elem.length; i++) {
            boolean flag = false;// 每趟排序都需要将 flag 设置为 false
            for (int j = 0; j < elem.length - i; j++) {
                if (elem[j] > elem[j + 1]) {
                    swap(elem, j, j + 1);// 调用上面写的交换方法
                    flag = true;// 发生交换 flag 更新为 true
                }
            }
            if (!flag) { // 如果 flag 还是为 false 则代表没发生交换,也就代表当前元素是有序的
                break;
            }
        }
}

最好有序n-1次，最坏逆序n(n-1)/2次

O(n²)  O(1)  稳定

 

2.简单选择排序

基本思想：通过n-i次关键字间的比较，从n-i+1个记录中选出关键字最小的记录，并和第i（1<=i<=n）个记录交换。

public void selectSort(int[] elem) {
    for (int i = 0; i < elem.length; i++) {
        for (int j = i + 1; j < elem.length; j++) {
            if (elem[i] > elem[j]) {
                swap(elem, i, j);// 调用上面写的交换方法
            }
        }
    }
}

比较n(n-1)/2次，最好交换0次，最差交换n-1次

O(n²)  O(1)   不稳定

 

3.直接插入排序

基本思想：将一个记录插入到已经排好序的有序表中，从而得到一个新的、记录数增1的有序表。

public void insertSort(int[] elem, int start, int end) {
    for (int i = start + 1; i <= end; i++) {
        int tmp = elem[i];
        int j = i - 1;
        while (j >= 0) {
            if (elem[j] > tmp) {
                elem[j + 1] = elem[j];
            } else {
                break;
            }
            j--;
        }
        elem[j + 1] = tmp;
    }
}

最好(n-1)(Σi)次，最坏(n+2)(n-1)/2次

O(n²)  O(1)   稳定

 

4.希尔排序

基本思想：把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至 1 时，整个文件恰被分成一组，算法便终止。

public void shell(int[] elem, int gap) {
    for (int i = gap; i < elem.length; i++) {
        int tmp = elem[i];
        int j = i - gap;
        for (; j >= 0; j -= gap) {
            if (elem[j] > tmp) {
                elem[j + gap] = elem[j];
            } else {
                break;
            }
        }
        elem[j + gap] = tmp;
    }
}
 
public void shellSort(int[] elem) {
    int gap = elem.length;
    while (gap > 1) {
        gap = gap / 3 + 1; // 希尔排序的增量是不确定的
        shell(elem, gap);
    }
}

O(n^3/2)   O(1)   不稳定

 

5.堆排序

基本思想：将待排序的序列构造成一个大顶堆（小顶堆），此时整个序列的最大（小）值就是堆顶的根结点。将它移走，然后将剩余的n-1个序列重新构造成一个堆，这样就会得到n个元素中的次大（小）值。如此反复执行，便能得到一个有序序列。

// 向下调整代码
public void adjustDown(int[] elem, int parent, int len) {
    int child = 2 * parent + 1;
    while (child < len) {
        if (child + 1 < len && elem[child] < elem[child + 1]) {
            child++;
        }
        if (elem[parent] < elem[child]) {
            swap(elem, child, parent);
            parent = child;
            child = parent * 2 + 1;
        } else {
            break;
        }
    }
}
// 建堆代码
public void createHeap(int[] elem) {
    for (int i = (elem.length - 1 - 1) / 2; i >= 0; i--) {
        adjustDown(elem, i, elem.length);
    }
}
 
// 堆排序
public void heapSort(int[] elem) {
    createHeap(elem);
    int len = elem.length - 1;
    //从后往前调整
    while (len > 0) {
        //交换堆顶和堆尾的元素
        swap(elem, 0, len);
        //重新调整
        adjustDown(elem, 0, len);
        len--;
    }
}

升序大堆，降序小堆

O(nlogn)  O(1)  不稳定

 

6.归并排序

基本思想：将一个有n个记录初始序列看作n个有序的子序列，然后两两归并，使子序列间有序，如此往复。

public void mergeSort(int[] elem) { 
　　mergeSortInternal(elem, 0, elem.length - 1); 
}

// 切割操作
public void mergeSortInternal(int[] elem, int start, int end) {
    //递归终止条件，拆分到只有一个数的时候停止递归
    if (start >= end) {
        return;
    }
    //选出中间下标作为拆分基准
    int mid = start + (end - start) / 2;
    //递归拆分
    mergeSortInternal(elem, start, mid); // 左区间
    mergeSortInternal(elem, mid + 1, end);// 右区间
 
    //切割完成后进行合并
    merge(elem, start, mid, end);
}

// 合并操作
public void merge(int[] elem, int low, int mid, int high) {
    //用一个临时数组用来交换顺序
    int[] tmp = new int[high - low + 1];
 
    int s1 = low; // 左区间开始位置
    int s2 = mid + 1; // 右区间开始位置
 
    int k = 0;//临时数组的索引开始位置
 
    // 比较两个区间中的元素
    while (s1 <= mid && s2 <= high) {
        if (elem[s1] <= elem[s2]) {
            tmp[k++] = elem[s1++];
        } else {
            tmp[k++] = elem[s2++];
        }
    }
    
    //循环结束两种情况
    //1、左区间还剩数值没有被放到tmp数组上
    while (s1 <= mid) {
        tmp[k++] = elem[s1++];
    }
    //2、右区间还剩数值没有被放到tmp数组上
    while (s2 <= high) {
        tmp[k++] = elem[s2++];
    }
    //将tmp数组的值放回到原数组中
    //[i+low] 就是当前的左区间下标开始位置
    for (int i = 0; i < tmp.length; i++) {
        elem[i + low] = tmp[i];
    }
}

O(nlogn)  O(nlogn)   不稳定

 

7.快速排序

基本思想：通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序的目的。

public void quickSort(int[] elem) { quick(elem, 0, elem.length - 1); }
private int partition(int[] elem, int low, int high) {
    int key = elem[low];//保存基准值，形成一个坑
    while (low < high) {
        //找比基准值小的值，记录该下标
        while (low < high && elem[high] >= key) {
            high--;
        }
        //找到后将左边形成的坑放置比基准小的值，此时右边就新形成了一个坑
        elem[low] = elem[high];
        //找比基准值大的值，记录该下标
        while (low < high && elem[low] <= key) {
            low++;
        }
        //找到后将右边形成的坑放置比基准大的值，此时左边就新形成了一个坑
        elem[high] = elem[low];
    }
    //low 和 high相遇时，一定是个坑，此时将基准放到low下标处
    elem[low] = key;
    return low;
}
 
private void quick(int[] elem, int start, int end) {
    //递归结束条件
    if (start >= end) {
        return;
    }
    
    int pivot = partition(elem, start, end); // 拿到基准值位置
 
    quick(elem, start, pivot - 1); // 在基准左边形成一个区间
 
    quick(elem, pivot + 1, end);    // 在基准右边形成一个区间
}

 

8.基数排序

以空间换时间

O(n+k)  O(n)  稳定

 

ps:参考链接 https://blog.csdn.net/qq_45270751/article/details/121066947