高数题目解法思路

第一章 函数、极限连续

1、夹逼定理求解

2、差分法求解

3、构造重要极限求解
最常见的就是构造那个等于e的
详情看纸质笔记本

4、等价无穷小

5、极限求不出来，一般情况是原式可以化简，直接因式分解或者凑项，然后消去

第二章 导数

不可导点个数的判断

函数\(f(x)=(1-cosx)|x^3-3x^2+2x|\)的不可导点的个数为2

判断方法：令绝对值中的函数为g(x),使之为0.求出来的x带入前面的函数，若是前面的函数也为0，则是可导点，反之为不可导点

第三章 不定积分与定积分

不定积分

1、换元
凑微分、换元
2、分部积分
公式见[[高数学习笔记#🎇利用分布积分法求不定积分]]
3、注意2倍角公式和角平方和公式的运用
有时候需要进行转换才可以利用，注意转换
4、最后一个C因为是任意常数，所以就怎么方便怎么来
有时候可能需要自己构造C
5、最后把那24个常见的不定积分给背下

6、分项积分法
尽量构造根号里复杂的式子，如下


若是有些算式不能直接构造微分，尝试从下面的括号中分离再构造，如下👇

✨构造的时候注意构造最复杂的，然后你会发现上面的东西都会被消掉，若是不能构造，尝试分离一下再构造
7、若是拆分很麻烦的话，不妨试一下添加，比如分数上下同时乘以相同的数或者凑一下平方差

定积分

1、注意不要先急着求函数，首先需要看一下是否可以后面直接使用导数

2、注意复和函数一定要求导，勿忘！！！

变限积分

• 变限积分在函数方程中求原函数

变限积分求导注意公式参考：[[高数定理集合#变限积分求导]]

对于变限积分的话可以设定积分为一个未知量A，然后进行积分求解

例题1：

解答：

• 变限积分求导数

当你的原函数求出来发现是0的时候注意这肯定是不对的，可以使用换元的方法尝试一下

eg：

广义积分

瑕积分

注意做题的时候范围内是否有没有定义的点，这一点就是瑕点，然后要从这点分开计算

无穷积分

一目了然，上下限中含无穷的

🐥有理函数求不定积分专项

一、解法通用思路

因式分解拆分示例：

二、常见的有理函数积分情形处理

情形一：上可化下导数

情形二：分子为常数，分母为2次函数形式

情形三：包含三角函数类型

方法一：待定系数法

ep：用在分式下面是两个三角函数相加的形式

eg：

方法二：二倍角

当分式下面只有一个三角函数的时候

eg：

方法三：上下同乘，构造平方差或者平方和

方法四：换元法

这个方法非常的实用，务必要记住⭐⭐⭐⭐⭐

eg：

这个x=2倍的那个，这里写错了

情形四：带根号的类型

方法一：考虑圆的面积的求法

方法二：直接换元换掉整的根号

方法三：根号中构造平方或者是构造平方和

区间在现

令x=上限+下限-t，然后换元带入求解

定积分的性质

1.线性性质：设\(f(x)\)和\(g(x)\)在区间\([a,b]\)上可积，\(k_1,k_2\)为任意常数，则$$\int_a^{b(k_1f(x)+k_2g(x))dx=k_1\int_a}bf(x)dx+k_2\int_a^bg(x)dx$$

2.区间可加性：设\(f(x)\)在区间\([a,b]\)上可积，\(c\in(a,b)\)，则$$\int_a^{bf(x)dx=\int_a}cf(x)dx+\int_c^bf(x)dx$$

3.估值定理：设\(f(x)\)在区间\([a,b]\)上连续，则存在\(\xi\in[a,b]\)，使得$$\int_a^bf(x)dx=f(\xi)(b-a)$$

4.积分第一中值定理：设\(f(x)\)和\(g(x)\)在区间\([a,b]\)上连续，\(g(x)\)不变号且不恒为\(0\)，则存在\(\xi\in(a,b)\)，使得$$\int_a^{bf(x)g(x)dx=f(\xi)\int_a}bg(x)dx$$

5.积分第二中值定理：设\(f(x)\)在区间\([a,b]\)上连续，\(m,M\)分别为\(f(x)\)在区间\([a,b]\)上的最小值和最大值，则存在\(\xi\in[a,b]\)，使得$$m(b-a)\leq\int_a^bf(x)dx\leq M(b-a)$$

🐥证明题解法

中值定理类的解法

罗尔中值定理解法

参考视频：B站视频

解题步骤：
1、构造辅助函数
2、带入点
3、求出导数
4、得证

题目样例：类似如下基本上都是罗尔中值定理

✨如何构造辅助函数？

构造辅助函数的本质实际上是求原函数

方法一：求微分方程

• 这个方法一般是用在只有一个柯西的情况下，也是首选的方法

• 格式

\(化成f(x)=C的格式\)，也就是说右边只是一个常数

方法二：两边同时积分

次选方法，格式同上

不等式证明解法

解题步骤：
首先是移项--->然后是另左边所有为一个函数---->根据函数分类讨论x处于不同范围时的值---->也就是要求出单调递减和单调递增区间

例题一：

第四章 向量代数与空间几何

点到点的距离

点到直线的距离

设直线的方程为 Ax+By+C=0 ，平面上任意一点 \((x_0,y_0)\) 到该直线的距离 d 的公式为：

\[d=\frac {|Ax_0+By_0+C|} {\sqrt {A^2+B^2}} \]

直线与面的交点

设直线的方向向量为\(\{x_0,y_0,z_0\}\)，过的点为\((x_1,y_1,z_1)\)
列出直线的参数方程：\(x=x_0t+x_1,y=y_0t+y_1\)

点到面的距离

\[d=\frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}} \]

面到面的距离

直线与直线的距离

设一条直线上的一个点为M，另一条直线上的点为N，n向量为两个直线方向向量的向量积，两直线的距离就是 \(\frac{|\overrightarrow {MN}\cdot \overrightarrow {n}|}{|\overrightarrow {n}|}\)

向量的向量积和数量积的运算

向量的数量积运算规律

(1) 交换律a∙b=b∙a；

(2) 结合律(λa)∙b=a∙(λb)=λ(a∙b)；

(3) 分配律(a+b)∙c=a∙c+b∙c；

向量的向量积运算规律

(1) 反交换律\(aⅹb=-bⅹa\)；

(2) \(aⅹa=0\)；

(3) 结合律\((λa)ⅹb=aⅹ(λb)=λ(aⅹb)\)，其中λ为实数；

(4) 分配律\((a+b)ⅹc=aⅹc+bⅹc\).

⭐向量的混合积

公式如下：

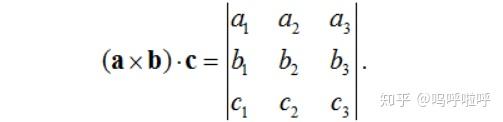
根据行列式的运算性质，可得向量的混合积满足轮换性，即

\({\vec{a} \cdot (\vec{b} \times \vec{c})}\)=\(\vec{b} \cdot (\vec{a} \times \vec{c})\)=\(\vec{c} \cdot (\vec{a} \times \vec{b})\)

例题：

第五章 无穷级数

幂级数

收敛域

收敛半径R

幂级数的收敛半径可以用根值测试来求。具体来说，设幂级数为 \(\sum_{n=0}^{\infty} a_n x^n\)，则它的收敛半径 \(R\) 满足：
 \(R=\lim_{n\to ∞}| \frac{a_n}{a_{n+1}}|\)

当\(R>x>-R\)时是绝对收敛的，当取到R或是-R的时候则不确定其敛散性

幂级数求和函数

第一种情况：等比级数的样子

第二种情况：全幂级数

第三种情况：奇幂级数

改写技巧：

参考链接：

https://www.bilibili.com/video/BV19Y4y1z7ah/?buvid=XYD0576DD82E6A9A4088F981E2E5534B8259F&is_story_h5=false&mid=jGNO3DynBwwSVRImjOKPVA%3D%3D&p=1&plat_id=122&share_from=ugc&share_medium=android&share_plat=android&share_session_id=d0e38698-8809-4c1b-875c-d12ee961259e&share_source=QQ&share_tag=s_i&timestamp=1677820211&unique_k=IISfdBC&up_id=505412533&vd_source=6a717407be105416bfd0c9030e5cf6f8

第六章 常微分方程

补充

• 需要掌握的一些基础

• 微分方程最高有几阶导，那么其通解有几个独立的常数字

一阶微分方程

可分离变量的求法

情形一：直接分离dy、dx，构造关于y的方程

eg：

情形二：需要构造x/y或者y/x的情况，构造好后换元

eg：

• 分析：可以发现题目中出现的x/y的分式，构造成这个形式，然后进行换元

一阶齐次方程

基础掌握

• 一般的形式：\(dy/dx+p(x)y=q(x),q(x)=0\)
• 一阶齐次线性微分方程的通解为\(y=C_e^{-\int p(x)dx}\)，其中\(C\)为任意常数。

情况一：需要构造x/y的形式，然后换元

情况二：关于x的方程(与常规的关于y的相反)

一阶非齐次方程

基础掌握

• 一般的形式：\(dy/dx+p(x)y=q(x),q(x)不等于0\)
• 求解公式：\(y=e^{-\int p(x)dx}(\int q(x)e^{\int p(x)dx}dx+C)\)

伯努利方程解法

二阶常系数线性微分方程

基础掌握

• 解的结构：
  1、非齐次的通解=齐次的通解+非齐次的一个特解(需要求出C)
  2、齐次通解是以线性无关的特解与独立的常数的线性组合
  线性指相除为一个常数，否则为非线性

二阶齐次求解

基础掌握

二阶非齐次求解

基础掌握

• 求解的公式以及情况讨论
  
• 常见的求解思路：
  求出齐次的通解-->根据具体情况设非齐次的特解的形式--->将特解的形式求导带入原来的方程求出一个特解--->非齐次特解和齐次通解相加

情形一：q(x)有两个形式相加

将他们分开讨论即可

eg：

情形二：q(x)为三角函数的形式求通解

eg：

提分视频学习

有理函数不定积分

https://www.bilibili.com/video/BV1UA41127tH/?spm_id_from=333.788&vd_source=6a717407be105416bfd0c9030e5cf6f8

专升本证明题总结

https://www.bilibili.com/video/BV1Am4y1R7q6/?spm_id_from=333.337.search-card.all.click&vd_source=6a717407be105416bfd0c9030e5cf6f8

反函数总结

反函数求导问题

原函数的导数和反函数的导数互为倒数

参考视频：
https://www.bilibili.com/video/BV1iT411e7e3/?spm_id_from=333.337.search-card.all.click&vd_source=6a717407be105416bfd0c9030e5cf6f8`

无穷小的比较

主要是看次数，次数高的为高阶的无穷小