Paper Reading ---- QFlex 3.0: Fast and Accurate ARM Server Simulation | Knowledge Points： 中心极限定理 ，正态分布，置信度，置信空间，抽样误差

image

from pixiv

image

from AGPC ’25

Simulator and Simulation

QEMU 并不是一个 cycle‑accurate timing simulator，而是一个 功能级（functional）ISA 模拟／动态二进制翻译（dynamic binary translation）工具。它的主要特点和定位可以这样概括：

  1. 功能级仿真（Functional Simulation）

    • QEMU 的核心是准确地模拟指令的行为——「这条指令在寄存器或内存上做了什么」——而不是去精确建模每条指令在硬件上花了多少时钟周期。
    • 它使用 Tiny Code Generator（TCG）将被模拟平台的二进制代码动态翻译成宿主机的本地二进制，从而极大地提升了模拟速度。

  2. 用户态 vs 系统态模拟

    • 用户态模式（user‑mode emulation）：只模拟单个用户进程的 ISA，调用系统调用时切换到宿主机内核。
    • 系统态模式（system‑mode emulation）：模拟整台机器，包括 CPU、内存、I/O 设备、BIOS/固件 等，可以在 QEMU 上直接启动一个完整操作系统。

  3. 时序模型非常粗略

    • 虽然 QEMU 为一些设备（比如定时器、中断）引入了事件队列，但它并不会把每条指令的执行拆成若干个周期去推进流水线，也不会模拟缓存层次、分支预测惩罚或总线仲裁带来的时延。
    • 因此不能用它来测 IPC、pipeline stalls、cache miss latency 等微架构级性能指标，只能信赖它给出的「功能正确性」结果。

  4. 对比其它模拟器

    模拟器类型 典型工具 特点
    功能级模拟 QEMU, Spike 快速、动态翻译／解释；不保证时序准确
    Cycle‑accurate 模拟 gem5 (Timing 模式)、SimpleScalar 精确到每个时钟周期；可做微架构级性能分析，但速度很慢
    Statistical 模拟 SMARTS, SimPoints 通过抽样或统计模型加速时序仿真；在精度和速度之间折中
    Transaction‑level 模拟 SystemC TLM 在功能模型基础上加事物级通信延迟；更适合系统级验证

结论：

  • QEMU = 功能级 ISA 模拟／动态二进制翻译器
  • 不是 cycle‑accurate 的 timing simulator。如果你需要精确评估指令在流水线、cache、互连网络上的时序行为，就要选择像 gem5 的 Full‑System Timing 模式、SimpleScalar 或者 Sniper 这类真正的时序仿真器。

时序仿真（timing simulation）是一种在电路或系统设计验证中，用来检查信号在真实延迟条件下的行为和交互是否符合预期的仿真方法。它与纯功能仿真（仅关注逻辑正确性，不考虑延迟）不同，主要特点和目的包括：

  1. 考虑实际延迟

    • 在时序仿真中，会为每个逻辑门、连线和时钟网络分配真实的延迟值（通常来自后仿真提取的 SDF 文件）。
    • 仿真器根据这些延迟，计算信号从输入到输出所需的时间，并检查是否会引起时序违例（如建立时间、保持时间冲突）。

  2. 验证时钟和时序约束

    • 时序仿真能验证时钟树分布、时钟偏差（clock skew）、抖动（jitter）等对系统时序的影响。
    • 检查触发器（FF）、锁存器（latch）和组合逻辑之间的路径延迟是否满足设计的最大/最小时序要求。

  3. 常见的仿真类型对比

    仿真类型 主要关注点 优点 缺点
    功能仿真 逻辑功能正确性 快速、易于发现逻辑错误 不保证时序正确性
    时序仿真 真实延迟下的时序行为 能发现时序违例、时钟相关问题 仿真速度慢、对仿真资源要求高
    统计仿真（Statistical） 在抽样或统计模型下估算性能 兼顾速度和精度，可做大规模设计评估 精度受模型假设影响
    性能仿真（Performance） 系统级性能指标（吞吐、延迟等） 验证系统级性能需求 通常不关注每个门级时序

  4. 流程示例

    1. 综合 (Synthesis)：生成门级网表，并提取门延迟。
    2. 布局布线 (Place & Route)：确定物理位置并提取连线延迟。
    3. 延迟注入 (SDF Annotation)：将后仿真提取的延迟数据注入到网表中。
    4. 时序仿真：运行仿真波形，检查是否有时序违例或逻辑功能偏差。

  5. 应用场景

    • ASIC/FPGA 设计的后仿真（post-place-and-route verification）。
    • 时钟域跨越（CDC）验证，检查不同域间的数据稳定性。
    • 高速接口（DDR、PCIe、Ethernet 等）设计，时钟精度和延迟至关重要。

小结：
时序仿真通过注入真实的门级和连线延迟，能帮助设计者在功能正确之外，进一步保证电路在实际工作条件下的时序安全性，避免因延迟和时钟问题导致的失效或不稳定。

在计算机体系结构研究中，Timing Simulation 指的是一种仿真方法论——它关注“按时序（时钟周期）准确地模拟各模块之间的延迟与交互”，以评估微架构级别的性能指标（例如 IPC、流水线气泡、缓存命中延迟等）。而一个 Timing Simulator（时序仿真器）则是“承载”这种仿真方法论的软件工具或框架。两者的关系和区别可以归纳如下：

  1. 定义对比

  • Timing Simulation（时序仿真）

    • 是什么？ 一种仿真策略/方法。

    • 特点：

      • 周期级或亚周期级 地跟踪指令执行或硬件事件。
      • 精确建模流水线阶段、缓存访问、总线仲裁、互连网络延迟、分支预测惩罚等。
      • 输出性能指标（IPC、吞吐率、延迟分布）和瓶颈分析数据。

    • 应用： 微架构设计探索、性能调优、验证各种硬件优化（比如不同深度的流水线、不同大小的缓存）。

  • Timing Simulator（时序仿真器）

    • 是什么？ 将 Timing Simulation 方法论付诸实践的软件系统。

    • 特点：

      • 提供事件驱动或周期驱动的仿真引擎，实现对处理器内各个功能单元、缓存层次、互联、外设等的建模。

      • 通常内置 ISA 模拟（functional simulation）能力，以及 时序模型（cycle‑accurate 或 cycle‑approximate）。

      • 可分为：

        • 全系统（Full‑System）仿真器：支持启动完整操作系统（Linux、RTOS 等）、驱动与外设交互——gem5 的 full‑system 模式就是典型代表。
        • 用户级或系统调用（Syscall‑Emulation）仿真器：只仿真单个用户进程，不加载完整 OS，适合快速验证应用逻辑。
  1. 关系

  • 方法 vs 工具

    • Timing Simulation 是“做什么”：要精确到周期来评估延迟和性能。
    • Timing Simulator 是“用什么来做”：实现这一方法的模拟器软件。

  • 模拟器类型决定可用的仿真模式

    • 不同的 timing simulator（如 gem5、SimpleScalar、Sniper、ZSim）在精度（cycle‑accurate vs cycle‑approximate）、速度（慢 vs 快）、功能（全系统 vs 应用级）上各有取舍，但它们核心都是为了执行 Timing Simulation。
  1. gem5 里的 Full‑System Timing 模式
  • Full‑System：可以像在真实硬件上一样，启动并运行 Linux 内核、驱动程序和多个用户进程，甚至模拟各类外设（网卡、磁盘控制器等）。
  • Timing 模式：gem5 会在每个仿真周期里精确地推进 CPU 的流水线状态、缓存层次状态，以及互联和外设的事件队列，从而产出精确的性能数据。

因此，gem5 的 Full‑System Timing Simulator 就是一个既能模拟完整系统软件栈，又能执行高精度时序仿真的工具——它把 Timing Simulation 这一方法论落实到对整机（包括 OS + 应用）的仿真上。

  1. 小结
维度 Timing Simulation Timing Simulator
本质 仿真方法论／策略 实现该策略的软件工具
关注 周期级／亚周期级延迟与硬件事件的精确 支持何种仿真模式（全系统 vs 应用级）、仿真精度和性能
典型例子 — gem5（Full‑System Timing）、SimpleScalar
  • Timing Simulation = “做时序级别的精确仿真”
  • Timing Simulator = “用某个软件来跑这种精确仿真”

Paper Summary

PPT

到底什么是中心极限定理？

参考：3Blue1Brown

我们以掷骰子为例，我们定义随机变量x为一次掷六面骰子得到的点数

注意随机变量x也是有概率分布的，此时我们很好获得其概率分布，最典型的概率分布如下：

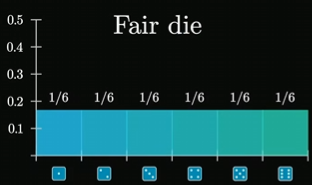
image-20250728193303797

当然我们可以在骰子上做些手脚，让其概率分布例如如下：

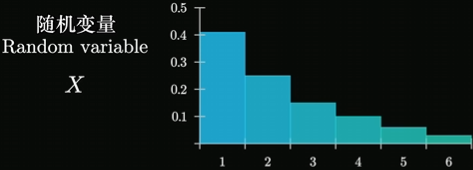
image-20250728193059406

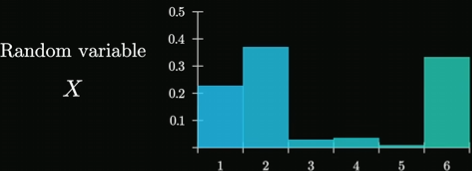
image-20250728193156025

但是不管随机变量x的初始概率分布是什么样的，我们选取n（n > 0）个骰子进行抛掷，并计算点数和

经过大量重复实验会发现点数和的分布符合正态分布

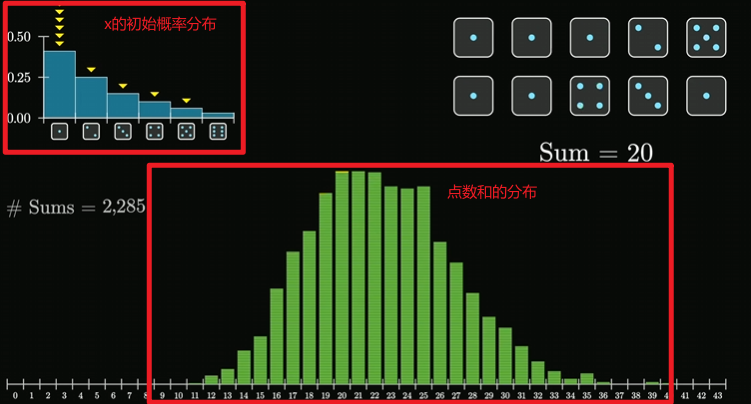
image-20250728193812650

期望(均值)，方差，标准差，与正态分布的性质

现在让我们来回顾下 期望(均值)，方差，标准差，与正态分布的性质

期望 \(\mu = E(X) = \sum_{x}P(X = x)x\)

在“有限总体”情形下，如果我们等概率抽取一个元素，那么每个 \(x_i\) 出现的概率都是

\(P(X = x_i) = \frac1N\)

于是用期望的定义：\(\mu = \sum_{i=1}^N P(X = x_i)\,x_i = \sum_{i=1}^N \frac1N\,x_i = \frac1N\sum_{i=1}^N x_i.\)

也就是说，当所有样本点概率相等时，“概率加权和”恰好退化为“算术平均”。

拓展：连续情形

在连续总体中，概率“密度”变成了 f(x)f(x)，数学期望要改用积分：

\(\mu = \int_{-\infty}^{+\infty} x\,f(x)\,\mathrm{d}x.\)

但核心思想一样：把每个可能的 xx 乘以它“出现的权重（概率或密度）”，再求和（或积分）。

期望（均值） \(\mu\) 表示分布的重心

  • 总体均值：总体中所有个体的真实平均值，是一个常数（通常未知）。记作\(\mu\)
  • 样本均值：从总体中随机抽取 n 个样本后的平均值，用来估计总体均值。记作\(\bar x\)
  • \(\bar x \;=\;\frac{1}{n}\sum_{i=1}^n x_i.\)

方差

  • 总体方差：总体中各数据点相对于总体均值的平均平方偏差，表示总体数据的离散程度。
    • 记作\(\sigma^2\)
    • $ \sigma^2 = \frac{1}{N}\sum_{i=1}^N (x_i - \mu)^2.$
  • 样本方差：本数据相对于样本均值的平均平方偏差，用来无偏估计总体方差。
    • 记作\(s^2\)
    • $ s^2 = \frac{1}{n-1}\sum_{i=1}^n (x_i - \bar x)^2.$

标准差：记作\(\sigma\), 表示分布的范围广度，标准差越大，分布越广（宽）

案例：

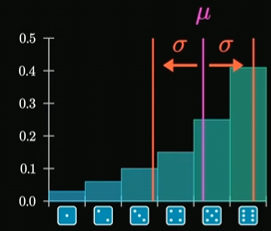
image-20250728200636525

image-20250728200701119

正态分布有**68–95–99.7 rule **

img

在正态分布中大约 68%、95%和 99.7%的值分别位于均值一个、两个和三个标准差范围内。

即可以理解为正态分布下任意一个随机变量\(X \backsim N(\mu, \sigma^2)\)有如下性质：

\(Pr[\mu - Z\sigma <= X <= \mu + Z\sigma] = 1 - \alpha\)

  • \(1-\alpha\) 就是置信度
  • \(Z\)是对应这个置信度的z值（z-score）常见取法：
    • 90% 置信度 → \(Z\approx1.645\)
    • 95% 置信度 → \(Z\approx1.96\)
    • 99% 置信度 → \(Z\approx2.576\)

68–95–99.7 rule 是一种粗略的经验法，精确还需要看具体的z值

好，回顾结束，现在让我想一下上述掷六面骰子，每次我们选择n个骰子进行重复实验，最终可以得到骰子点数总和的分布是正态分布的结论

正态分布也是有期望（均值）和 标准差的，那么随着n的变化，点数总和的分布会有什么变化呢？

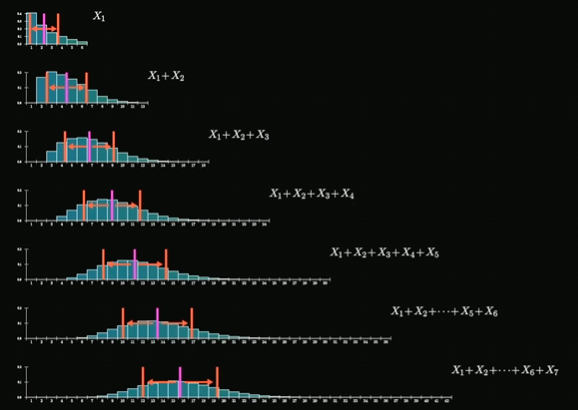
image-20250728200613744

答案是期望\(\mu\)越来越大，标准差\(\sigma\)越来越大； 从分布上的体现是越来越右移，越来越广(宽)，分布也越来越像正态分布了

有结论（要求随机变量x之间独立同分布）：

记：\(x_s = x_1 + x_2 +...+ x_n\)

那么：

  • \(\mu_s = n\mu, 其中\mu为x的初始分布的期望(均值)\)
  • \(\sigma_s^2 = n \sigma^2, 其中\sigma^2为x的初始分布的方差\)

那么\(\sigma_s = \sqrt{n} \sigma\)

从上我们可以得出：总和的分布变广(宽)的速度与参与求和的随机变量个数的平方根成正比

这里的“样本量 n”指的是你用来计算平均值的独立观察值的个数——不管你是一次性同时掷 n 个骰子，还是分 n 次掷一个骰子，数学上是等价的。

  1. 同时掷 n 个骰子
    • 你一次性拿 n 个骰子，同时掷出，得到的点数是一组 n 个独立的观测值。
    • 这组观测值的平均\(\bar X = \tfrac{1}{n}\sum_{i=1}^n\) \(X_i\) 随着 n 增大就会更接近正态分布。
  2. 分 n 次掷一个骰子
    • 你用同一个骰子连续投掷 n 次，记每次的点数为 \(X_1, X_2, \dots, X_n\)。
    • 再把这 n次点数求平均，同样 \(\bar X = \tfrac{1}{n}\sum_{i=1}^n X_i\)，随着 n 增大也会更接近正态分布。

两者在数学模型上完全一样：都是对同一分布（这里是“骰子点数，均匀分布在 1–6”）做 n 次独立采样，然后看它们的平均值。中心极限定理告诉我们：

\(\bar X = \frac{1}{n}\sum_{i=1}^n X_i \;\xrightarrow[n\to\infty]{d}\; N\bigl(\mu,\;\sigma^2/n\bigr)\)

所以关键在于“用于平均的独立样本个数”——这就是 n。无论你是一口气扔掉 n 个骰子，还是分 n 次扔同一个骰子，都是 n个独立样本。

拓展：重复这个实验

如果你想观察“平均值真的越来越像正态”的效果，通常会这样做：

  1. 固定一个 n（比如 10），
  2. 重复多次（比如做 1,000 次实验，每次都掷 10 次骰子，算一次平均），
  3. 把那 1,000 个平均值画成直方图，就能看到随着 n 从 10 → 30 → 100，直方图越来越像钟形曲线。

这里第二层“重复多次”只是用来可视化／估计分布，不是CLT里所说的样本量 n。CLT 关注的正是“每一次平均中用到的样本数” n。

置信度和置信区间

运用上述性质我们来解决一个现实问题：

image-20250728201851346

依据上述知识点可知：

  • 点数和的分布为正态分布

  • 假设骰子的初始分布为1~6点面出现概率均等，即：

    image-20250728193303797

    那么\(\mu = \frac{1}{6}(1+2+3+4+5+6) = 3.5\)

    \(\sigma = \sqrt{\frac{1}{6}((1-3.5)^2 + (2-3.5)^2 + ... + (6-3.5)^2)} = 1.71\)

  • 可得点数和的分布\(u_s = 100*\mu = 350 \\ \sigma_s = \sqrt{100}*\sigma = 17.1\)，即\(x_s \backsim N(\mu_s, \sigma_s^2)\)

  • 依据68–95–99.7 rule 这个区间应该为\([\mu_s - 2*\sigma_s, \mu_s + 2* \sigma_s]\) , 即 [316,384]

如何理解置信度？

上述说的 95%确定 就是置信度，会落在某个区间就是置信区间

置信度和置信区间还有更广泛的应用，常常用于用样本估计总体。

  • 点估计（Point Estimate): 点估计就是用样本统计量（如样本均值 \(\bar x\)、样本比例 \(\hat p\)、样本方差 \(s^2\) 等）去估计总体参数（如总体均值 \(\mu\)、总体比例 \(p\)、总体方差 \(\sigma^2\)）的一个“单一值”结果。例如：

    • 当我们想估计总体均值 \(\mu\) 时，常用的点估计就是样本均值

      \(\hat\mu = \bar x = \frac{1}{n}\sum_{i=1}^n x_i.\)

    • 想估计总体比例 p 时，用样本中“成功”次数除以样本容量 n：

      \(\hat p = \frac{\text{成功次数}}{n}.\)

  • 误差（Error / Margin of Error): 误差是指“点估计值”与“真实总体参数”之间的不一致程度，通常分为：

    1. 抽样误差（Sampling Error）：由于只观察了样本而非整个总体，产生的随机波动。

    2. 标准误（Standard Error, SE）：抽样误差的标准差，用来衡量点估计的变动大小。比如估计均值时

      \(\mathrm{SE}(\bar x) = \frac{\sigma}{\sqrt{n}}\)

      如果总体标准差 \(\sigma\) 未知，常用样本标准差 s 代替：

      \(\mathrm{SE}(\bar x)\approx\frac{s}{\sqrt{n}}.\)

    3. 置信区间半宽度（Margin of Error, MoE）：在给定置信水平（如 95%）下，用临界值（如正态分布的 \(z_{0.975}=1.96\) 或 t 分布的 \(t_{n-1,0.975}\)）乘以标准误，得到的“误差带”

    \(\mathrm{MoE} = z_{1 - \alpha/2}\times \mathrm{SE}.\)

  • 置信区间: 置信区间（Confidence Interval）确实通常写作 \([\;\text{点估计} - \mathrm{MoE},\;\; \text{点估计} + \mathrm{MoE}\;].\)

    例如，要构造总体均值的 95% 置信区间： \(\bigl[\;\bar x - z_{0.975}\,\tfrac{s}{\sqrt n},\;\;\bar x + z_{0.975}\,\tfrac{s}{\sqrt n}\bigr].\)

    • 如果总体分布未知但样本量 \(n\) 足够大（通常 \(n\ge30\)），根据中心极限定理，\(\bar X\) 仍近似正态，可近似使用 \(z\)。
    • 若总体标准差未知且样本量较小，则需用 Student’s \(t\) 分布的临界值 \(t_{n-1,\,1-\alpha/2}\)。

要理解置信区间，就要从统计学最基本最核心的思想去思考，那就是

用样本估计总体。

比如抽样调查会员满意度，结果是满意度为80%，误差为正负5%，置信度是95%。这一结果意味着3点：

1）样本中的满意度是80%，这是用样本对总体的点估计

2）点估计的范围是区间（75%，85%）

3）如果用类似的方法，重复抽取大量（样本量相同）样本时，产生的大量类似区间中有些会覆盖真正的总体参数值（即总体满意度），而有些不会，但其中大约有95%会覆盖真正的总体参数值。

对某个参数（如总体均值 \(\mu\) 或总体比例 \(p\)）的点估计值（样本均值 \(\bar{X}\) 或样本比例 \(\hat{p}\)），我们希望给出一个区间：

\(\bigl[\text{点估计} - E,\;\text{点估计} + E\bigr]\)

使得这个区间“以 \(1−α\) 的概率”覆盖真参数。这里的 E 就是误差，它度量了我们在该置信水平下，可能偏离真实值的最大幅度。

误差在统计学上就是置信区间的半宽度\(MoE\)

我们也很快能够在知道误差E的最大限度下，在指定的置信度下反所需的样本量n:

假设在95%置信度下，要求抽样误差最大不超过5%，那么

\(z_{1-\alpha/2} * SE = z_{0.975} * \frac{s}{\sqrt{n}} = E <= 0.05\)

上述内容其实也可以按照我们掷骰子的案例进行理解：

我们选取n（n > 0）个骰子进行抛掷，并计算点数和的平均，经过大量重复实验会发现点数和平均的分布符合正态分布：

我们知道点数和的分布$u_s = n\mu \ \sigma_s = \sqrt{n}\sigma $

点数和平均的分布为$u_a = \mu \ \sigma_a = \frac{\sigma}{\sqrt{n}} \(， 即\)\bar{x} \backsim N(\mu_a, \sigma_a^2)$ (\(\mu,\sigma\)为骰子初始分布的期望和标准差)

有没有感觉点数和平均的分布的标准差和上述的标准误公式是一样的？对，下面还有更巧的：

依据正态分布的性质应该有：

\(Pr[\mu_a - Z\sigma_a <= \bar{x} <= \mu_a + Z\sigma_a] = 1 - \alpha\)

我们变化下上面的公式可以得到：\(Pr[\bar{x} - Z\sigma_a <= \mu_a <= \bar{x} + Z\sigma_a] = 1 - \alpha\)

上述掷骰子的案例，若骰子的初始分布我们未知，我们只能通过点估计用 \(样本标准差s代替总体标准差\sigma\)，所以在95%置信度下，置信区间为 \(\bigl[\;\bar x - z_{0.975}\,\tfrac{s}{\sqrt n},\;\;\bar x + z_{0.975}\,\tfrac{s}{\sqrt n}\bigr].\)

现在我们能够解决一个更加困难的问题了：

目前端到端时序仿真采集性能指标U-IPC过慢（因为全程端到端进行时序仿真太慢了），我现在选择n个抽样节点进行时序仿真，其余时间进行功能仿真以加速仿真采集性能指标U-IPC的过程

现在我希望仿真抽样得到的 U‑IPC 平均值 与 端到端时序仿真得到的 U‑IPC 真值 之间的 相对误差在95%的置信度下控制在5%, 求抽样节点n应该满足什么条件？

  • 绝对误差（Absolute Error）: 估计值 \(\bar x\) 与“真实值”或参考值 \(\mu_x\) 之间的直接差距，不考虑量级或比例关系。

  • \[\text{绝对误差} = \bigl|\bar x - \mu_x\bigr|. \]

  • 相对误差（Relative Error）: 把绝对误差归一化到真实值的比例，反映误差在整体量级里所占份额。

  • \[\text{相对误差} = \frac{\bigl|\bar x - \mu_x\bigr|}{\mu_x} \]

答案是：

\[n >= (\frac{Z}{\epsilon}V_x)^2 \\ 其中V_x = \frac{\sigma_x}{\mu_x} 被测性能指标 𝑥（如 U‑IPC）的 变异系数（coefficient of variation） \\ \epsilon 取 5\% \\ Z 取 Z_{0.975} = 1.96 \]

推理：

若我们对 \(n\) 个独立样本测得指标值 \(x_1,\dots,x_n\)，它们的样本平均 \(\bar x\) 的标准差（标准误差）是

\[\mathrm{SE}(\bar x) = \frac{\sigma_x}{\sqrt{n}}. \]

正态分布性质告诉我们：

\[\Pr\Bigl[\,\mu_x - Z\cdot\mathrm{SE}(\bar x) \le \bar x \le \mu_x + Z\cdot\mathrm{SE}(\bar x)\Bigr] = 1-\alpha. \\ \Pr\Bigl[\,\bar x - Z\cdot\mathrm{SE}(\bar x) \le \mu_x \le \bar x + Z\cdot\mathrm{SE}(\bar x)\Bigr] = 1-\alpha. \\ 可得在95\%置信度下会有： \\ \bigl|\bar x - \mu_x\bigr| \leq Z\cdot\mathrm{SE}(\bar x) \]

令置信度 \(1-\alpha=95\%\)，则 \(Z=1.96\)。

因为：

\[\epsilon = \frac{\bigl|\bar x - \mu_x\bigr|}{\mu_x} \\ 为了确保当\epsilon取5\%时应该是远远足够了的，即 \\ \bigl|\bar x - \mu_x\bigr| \leq \epsilon\mu_x \]

即：

\[Z\cdot\mathrm{SE}(\bar x) \leq \epsilon\mu_x \\ Z\cdot\frac{\sigma_x}{\sqrt{n}} \leq \epsilon\mu_x \\ n >= (\frac{Z}{\epsilon}V_x)^2 \]

Derivation:

Suppose we take \(n\) independent samples of the metric, obtaining values \(x_1, x_2, \dots, x_n\). Their sample mean \(\bar x\) has standard deviation (standard error)

\[\mathrm{SE}(\bar x) \;=\; \frac{\sigma_x}{\sqrt{n}}. \]

By the properties of the normal distribution, we have

\[\Pr\Bigl[\mu_x - Z\,\mathrm{SE}(\bar x) \;\le\; \bar x \;\le\; \mu_x + Z\,\mathrm{SE}(\bar x)\Bigr] = 1-\alpha, \]

which is equivalent to

\[\Pr\Bigl[\bar x - Z\,\mathrm{SE}(\bar x) \;\le\; \mu_x \;\le\; \bar x + Z\,\mathrm{SE}(\bar x)\Bigr] = 1-\alpha. \]

Thus, at a 95% confidence level we have

\[\bigl|\bar x - \mu_x\bigr| \;\le\; Z\,\mathrm{SE}(\bar x). \]

Setting the confidence level \(1-\alpha=95\%\) gives \(Z = 1.96\).

Next, define the relative error \(\epsilon\) by

\[\epsilon \;=\; \frac{\bigl|\bar x - \mu_x\bigr|}{\mu_x}. \]

If we wish to bound the relative error by 5%, we require

\[\bigl|\bar x - \mu_x\bigr| \;\le\; \epsilon\,\mu_x. \]

Combining with the previous inequality,

\[Z\,\mathrm{SE}(\bar x) \;\le\; \epsilon\,\mu_x \quad\Longrightarrow\quad Z\,\frac{\sigma_x}{\sqrt{n}} \;\le\; \epsilon\,\mu_x. \]

Rearranging to solve for \(n\) yields

\[n \;\ge\; \biggl(\frac{Z}{\epsilon}\,V_x\biggr)^2, \]

where \(V_x = \sigma_x / \mu_x\) is the coefficient of variation.

posted @ 2025-07-29 19:42  次林梦叶  阅读(11)  评论(0)    收藏  举报