并行计算架构和编程 | Parallel Programing

image

from pixiv

Parallel Programing Basics

Creating a parallel program

并行加速比的下限：Amdahl’s Law（阿姆达尔定律）

并行程序的宏观思考过程可总结如下：

  • 挖掘工作可并行的部分。
  • 划分工作。
  • 管理数据的方面，沟通，同步。

最初我们计算并行效率可通过如下公式：

\(Speedup (Pprocessor) = \frac{Time(1 Processor)}{Time(P Processor)}\)

我们能够依据Amdahl’s定律得知\(Speedup\)是有上限的，定义\(S\)为不可并行执行占总顺序执行的比例，那么：

\(Amdahl’s Law = \frac{1}{s+\frac{1-s}{p}}\)

举例

先需要对一个\(N * N\)的图片进行如下两个步骤：

  1. 提高图片每一个像素的亮度至两倍
  2. 对图片全部像素求平均

我们可以很容易此种方法：对于步骤1无数据依赖完全可并行，对于步骤2可以先P个线程分别并行求和某一块区域，最终将P块区域的和相加，求平均。那么就有下图所示：

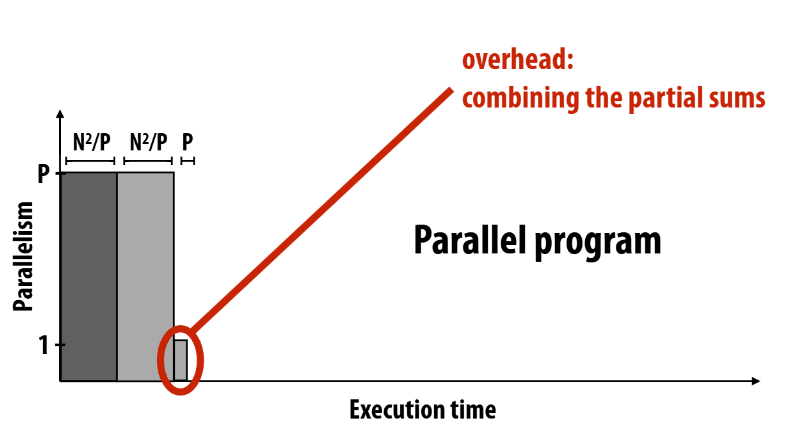
image-20250309213226775

其中\(S = \frac{p}{2^n}\), \(Speedup <= \frac{2n^2p}{p^2+2n^2-p}，当n>>p时，Speedup <= 1\)

并行加速比的上限: Gustafson's law(古斯塔夫森定律)

深入研究阿姆达尔定律和古斯塔夫森定律

Parallel Programming Process

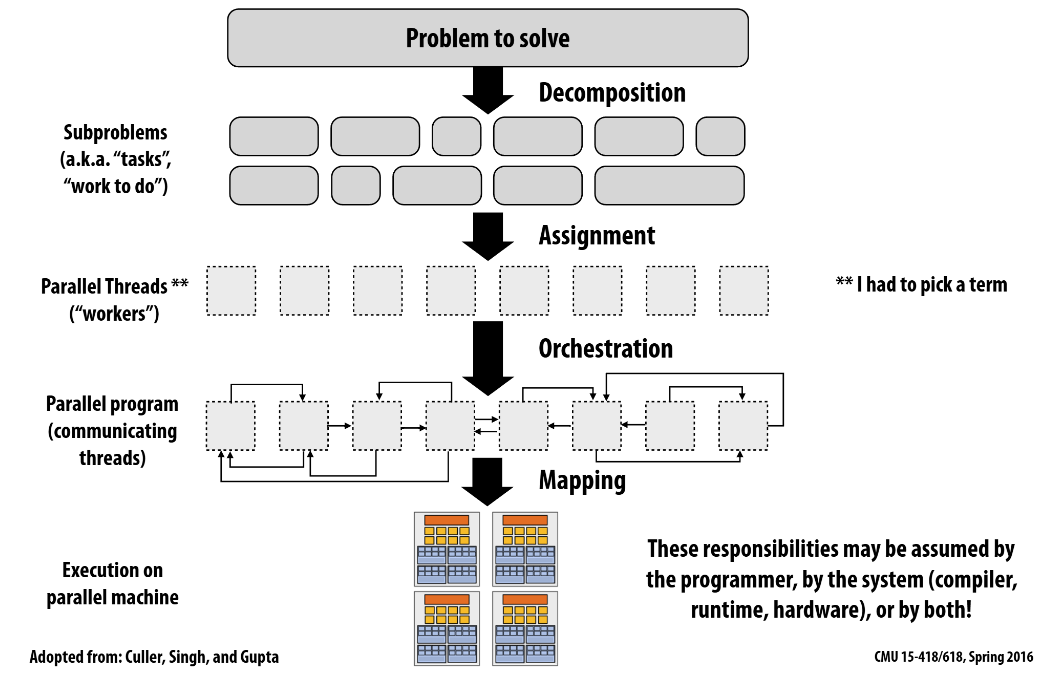
image-20250309214120208

  • Decomposition(分解)：将原问题分解为许多子问题（tasks），这个过程需要思考依赖关系，最好能够分解出足够的子问题让全部的执行部件处于忙碌状态
  • Assignment(分配)：将子问题分配给线程进行执行，这个过程需要思考负载均衡，减少消息传递消耗（communication costs）
    • 静态分配：硬编码分配方式，指定tasks给线程执行
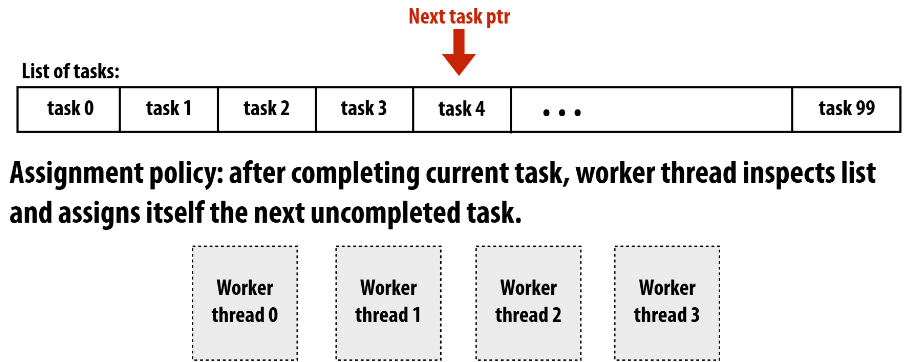
    • 动态分配：运行时决定线程执行哪些tasks，比如将tasks装入queue，线程执行完task后再从queue中取出task，一般不会有太差的负载均衡

​ image-20250309220716737

  • Orchestration(编排)：需要考虑组织消息传递，同步，保持较好的局部性
  • Mapping(映射)：将线程的工作映射到处理器执行单元上，一般不是程序员需要考虑的事情，一般由操作系统，编译器，硬件（CPU,GPU）决定

A parallel programming example

算法执行Gauss - Seidel sweeps

$Gauss-Seidel \ sweeps更新方式: A[i,j] = 0.2 * (A[i, j] + A[i,j - 1] + A[i - 1, j] + A[i, j + 1] + A[i + 1, j]) $， 数据依赖如下：(回想下PLCS问题，其LCS普通算法数据依赖很像这个)

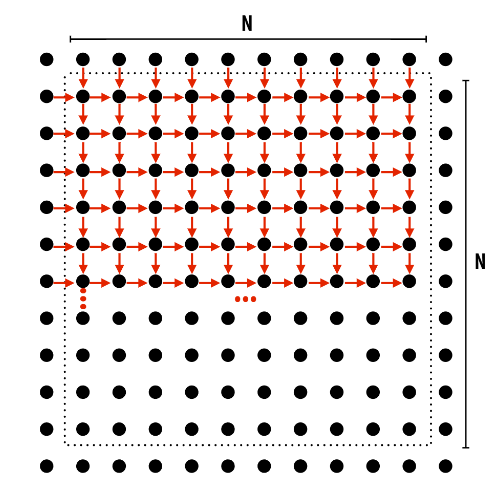
image-20250309221953997

对于这个算法，我们挖掘其中的可并行性，发现对角线上的元素无数据依赖：

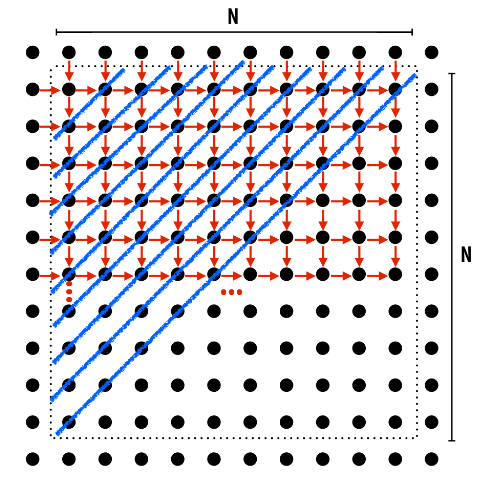
image-20250309222132625

但是这依旧有许多问题：

  • 负载不均衡：每个对角线上需处理的元素个数偏差较大
  • 局部性差
  • 需要同步

换个算法吧，我们需要让生活更美好更简单一点：红黑排序

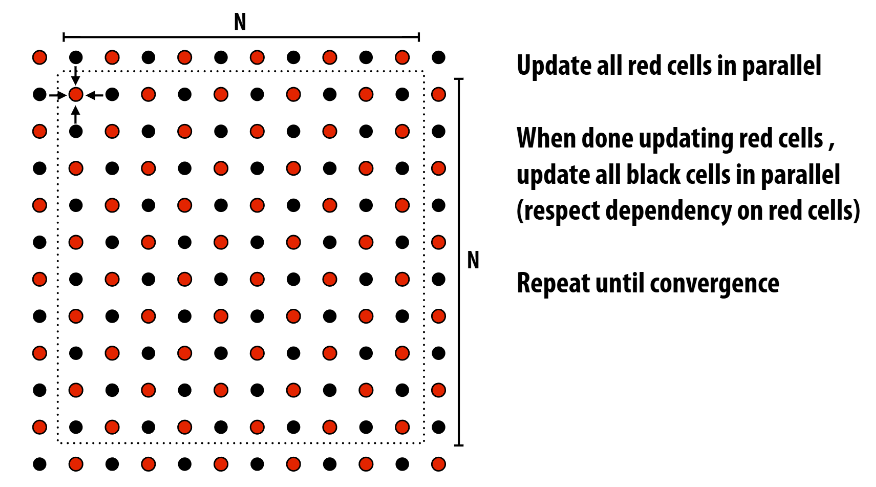
image-20250309223119928

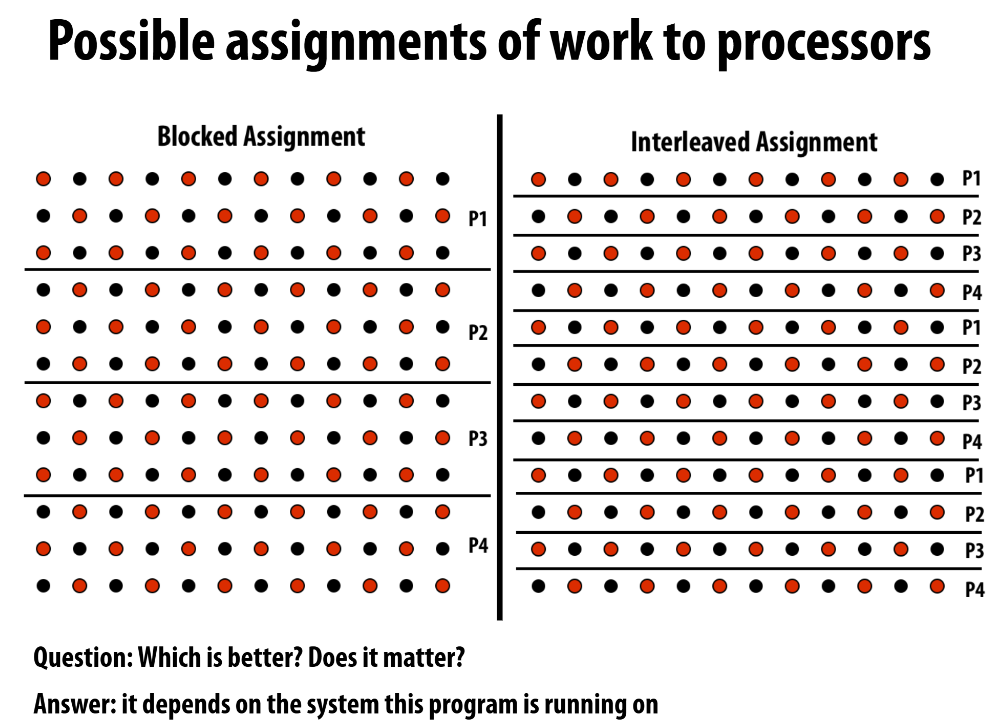
image-20250309223423325

为什么说要取决于程序运行在哪个机器上呢？

需要注意边界情况，当程序运行在Message passing Model时，因为数据在不同的机器/处理器上，边界数据传递需要开销，那么边界越多开销也越大

Work Distribution and Scheduling

Assignment

Static Assignment

  • 优点：减少了运行时动态分配所需的额外计算。
  • 缺点：容易负载不均衡。尽管我们静态分配看起来分配平均，但可能总有某些任务运行的时间很长。
  • 适合静态分配的场景：
    • work num和work execution time已知或可预测
    • work num已知，work execution time未知但其统计分布可知

Dynamic Assignment
实现方式之一就是任务队列和线程池了，be like:
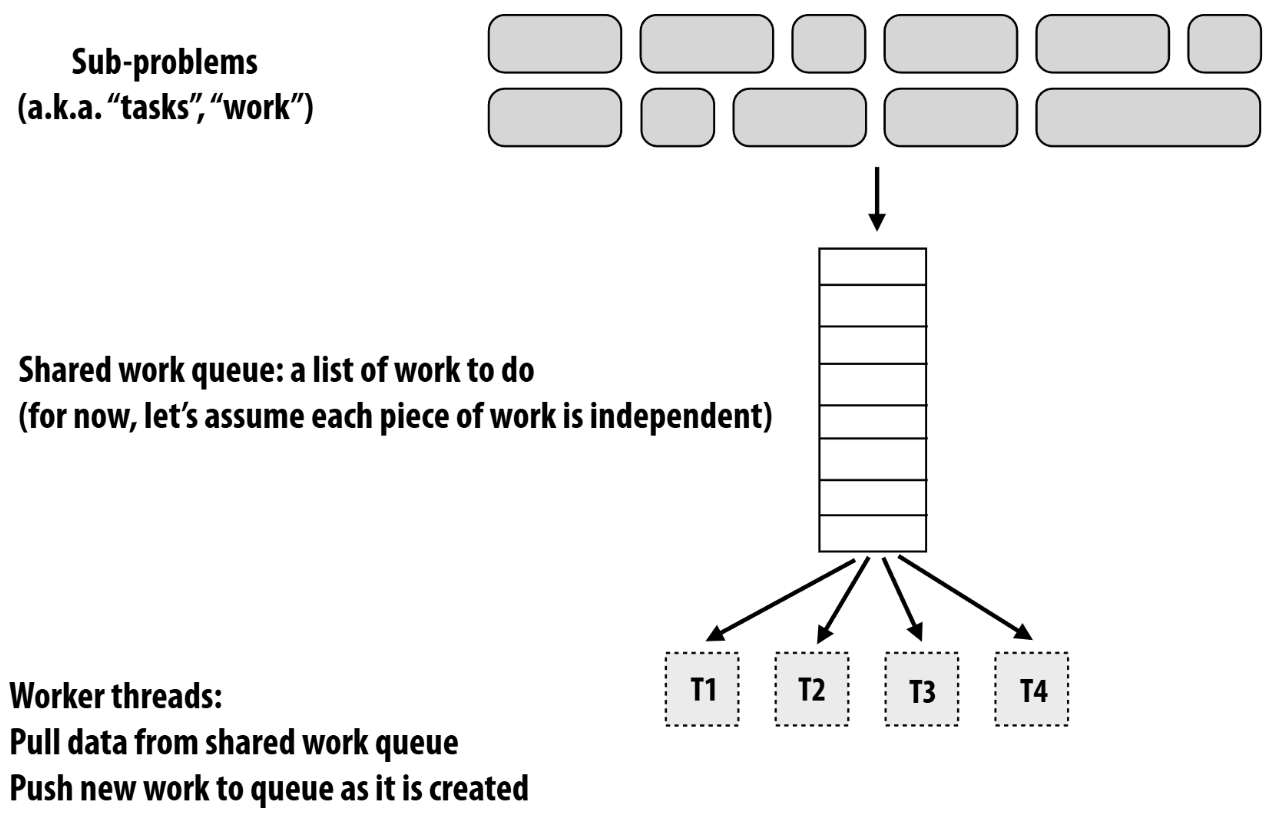
image

  • 优点：很好地缓解了负载不均衡的问题，不管任务执行时间长短，线程执行完即可继续到任务队列中获取任务执行。（当然这需要一点额外任务的安排，下面将会讲解）
  • 缺点：锁的竞争。在任务队列中获取任务涉及到同步，通信等问题，情况可能be like:
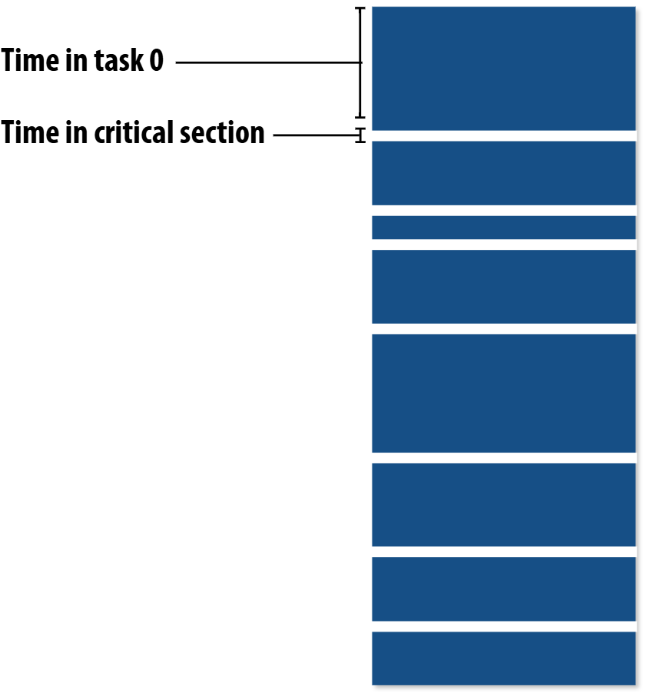
    image
    critical section即临界区，可以看到上图中有很多临界区的开销。
    • 大颗粒度的任务划分解决临界区开销，但是会引入负载不均衡的问题。
    • 小颗粒度的任务划分解决负载不均衡，但是会引入更对临界区的开销。

所以我们需要一些聪明的任务划分方法，经验告诉我们：先划分为大颗粒度，再不断细化为小颗粒度，大颗粒度任务优先执行

上述问题的主要来源是只有一个任务队列，那么我们拥有Distributed work queues不就解决了这个问题吗？be like:
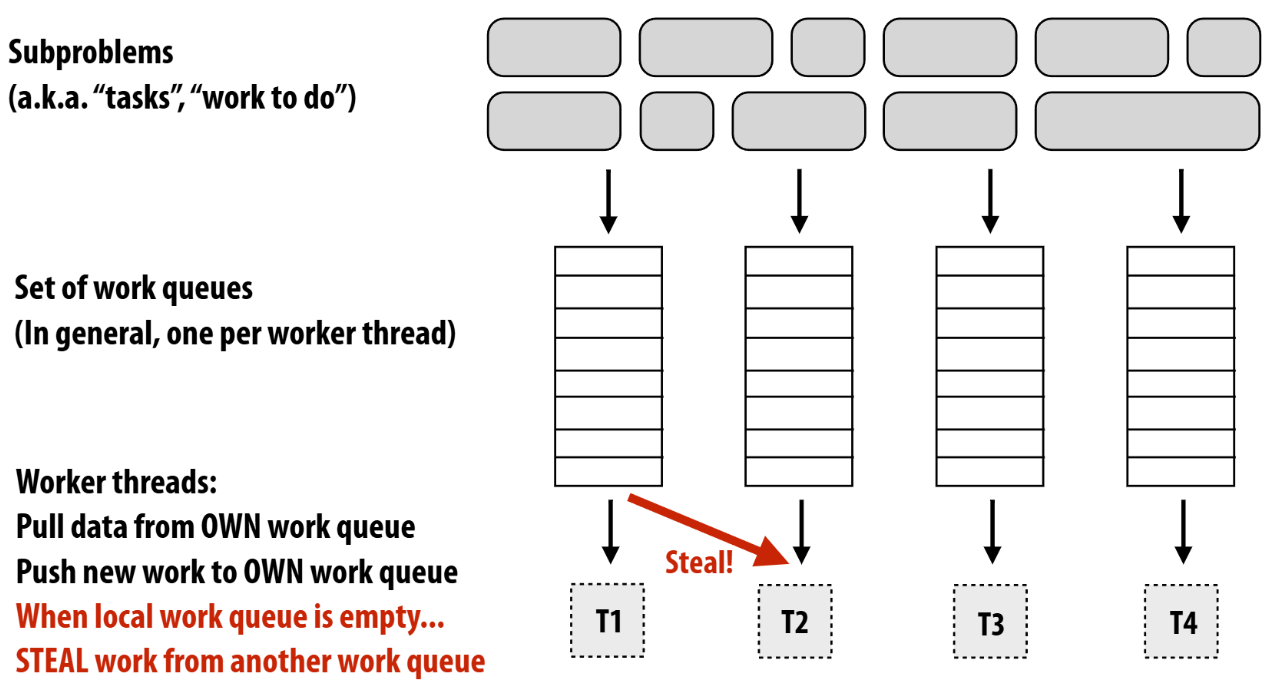
image

对于steal还有很多问题有待解决：1. 从哪个任务队列中steal? 2.steal多少？...

fork-join parallelism

Common parallel programming patterns

  • Data parallel. such as: ISPC foreach, ISPC bulk tasj launch

  • 用线程显示地管理并行，such as C code with pthreads

    • 需要注意的是这种方式会导致每一个thread占用一个core(如果是超线程的话，两个thread占用一个core)。
    • 当显示创建的软件线程超过了硬件线程，那么软件线程会抢占硬件资源，导致上下文管理花费较高。

fork-join parallelism是一种隐式的基于线程管理并行的方式。典型运用场景为需要用分治算法解决的问题。be like:

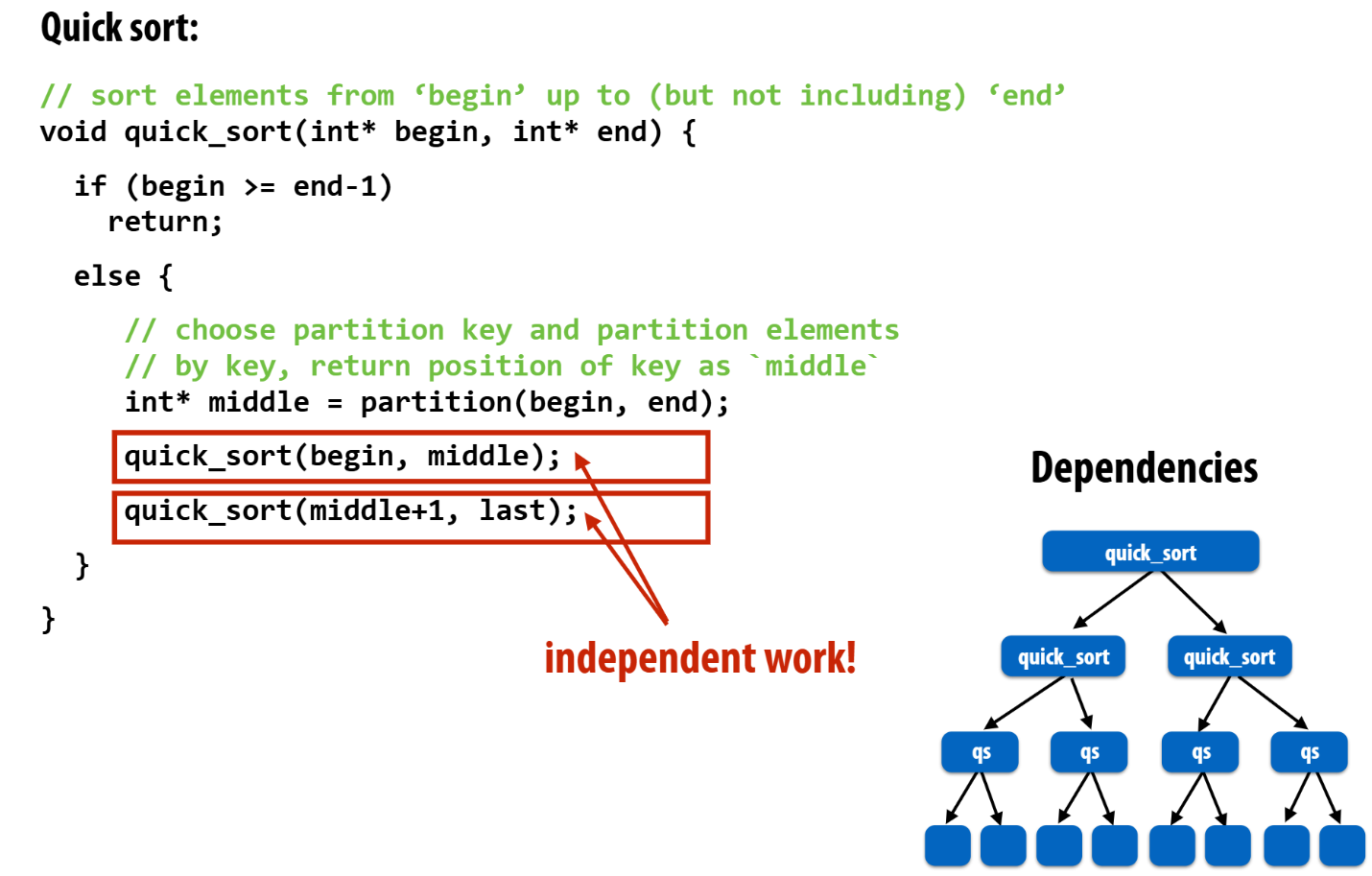
image

抽象实现
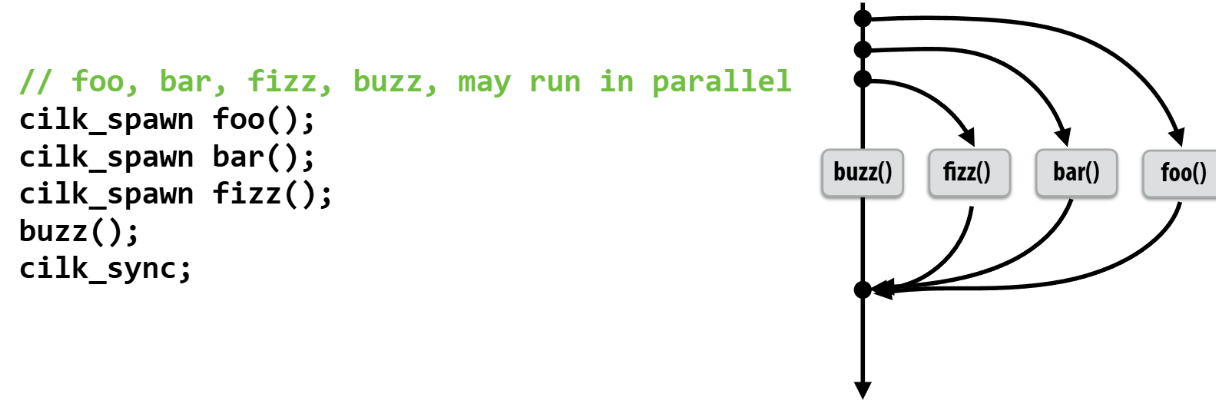
image
逻辑效果
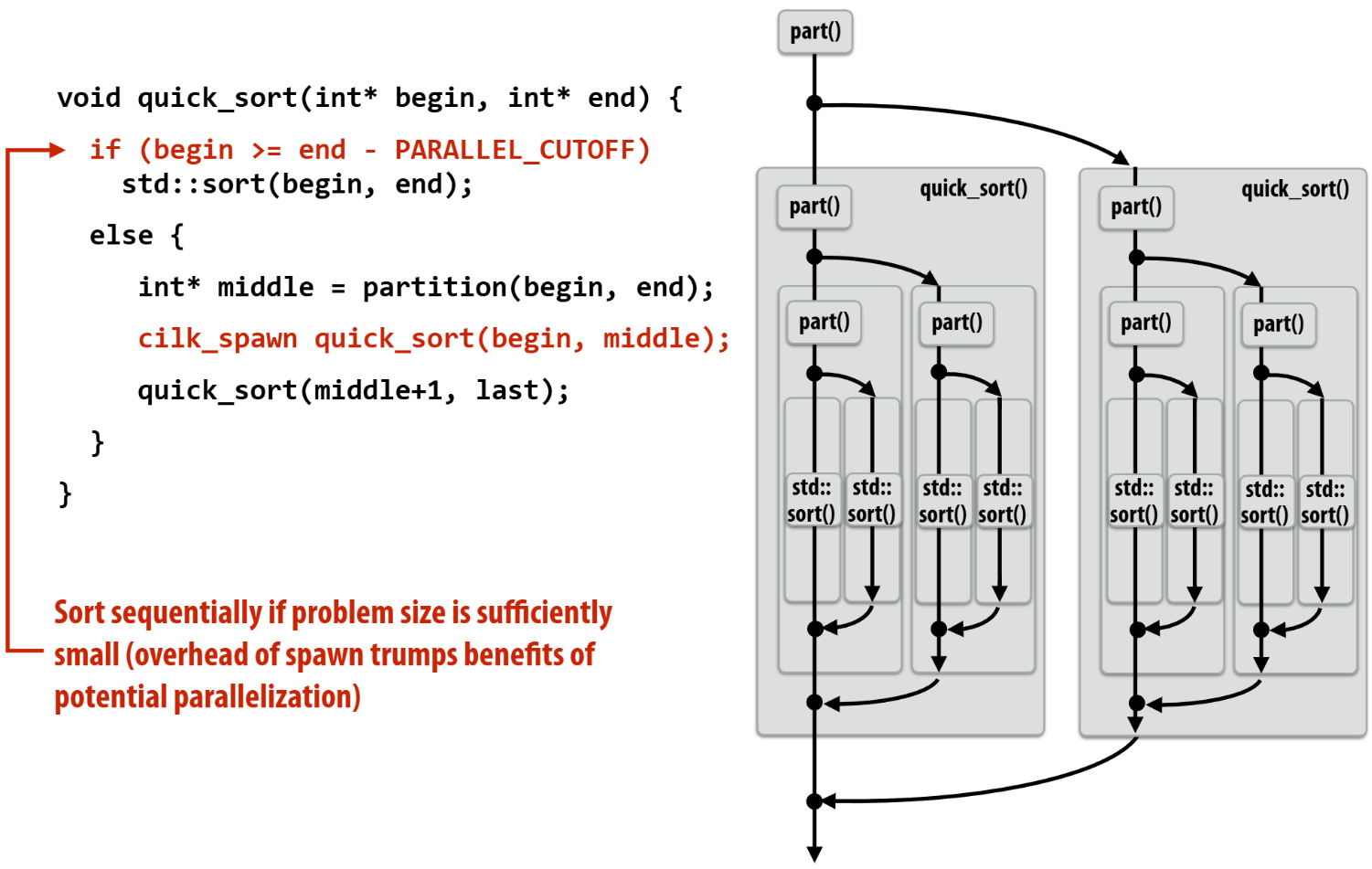
image
具体效果
image
具体实现
实现思路即上述提及到的Distributed work queues + threads pool

数据并行（Data Parallelism）

并行计算模式（Parallel Patterns）是一组可复用的设计方案，用于组织并行算法的结构，以提升可扩展性和性能。

并行模式大致可分为两类：

  • 任务并行（Task Parallelism）：将一个大任务递归或系统地拆分为多个子任务，分别并行处理，再将结果汇聚。这类模式包括 Fork–Join 和 Branch-and-Bound 等。

  • 数据并行（Data Parallelism）：对大规模数据集合执行相同的操作，每个数据元素或块独立并行地被处理，常见模式有 Map、Reduce、Scan 等。

    理论知识

    介绍了相关优化知识

Map 模式

Map 模式对集合中每个元素执行相同的操作，完全独立，典型实现为并行 for-loop。每次迭代互不依赖，易于在多处理器上分配。例如，将数组中每个元素乘以常数、图像像素滤波等。

parallel_for(i = 0; i < N; ++i)
  B[i] = f(A[i]);

Reduce 模式

Reduce（规约）模式将集合中的所有元素通过某个二元操作（如求和、最大值）合并为单个结果。并行实现通常先将数据分块，在各自块内完成局部规约（local reduction），然后再将所有局部结果汇总（global reduction）。

形式化定义：给定二元函数 ⊕、输入集合 A[0..n) 和初始值 b0，最终结果

b = A[0] ⊕ (A[1] ⊕ ( ... ⊕ (A[n-1] ⊕ b0)...))

Scan（Prefix Sum）模式

Scan（前缀和或前缀运算）与 Reduce 类似，但输出一个与输入等长的数组，其中每个元素 S[i] 是前 i 个元素规约的结果。即

S[0] = b0
S[i] = S[i-1] ⊕ A[i-1],  for 1 ≤ i ≤ n

并行实现典型算法（Blelloch scan）分为上升（up-sweep）和下降（down-sweep）两个阶段，时间复杂度为 O(log n)，适用于 GPU 和多核 CPU。

Assagement 3的作业即是完成Scan

posted @ 2025-03-27 22:00  次林梦叶  阅读(59)  评论(0)    收藏  举报