JXNU数据库----关系数据理论

from pixiv

---

基本概念

• 关系 P40

  D1xD2x...xDn 的子集叫做在域D1，D2，...,Dn 上的关系

• 关系模式 P42

  在关系数据库中，关系模式是型，关系是值，关系模式是对关系的描述
  现实世界随着时间在不断地变化，因而在不同时刻关系模式的关系也会有所变化，但是已有的事实和规则限定了关系模式所有可能的关系必须满足一定的完整性约束条件

  关系的描述称为关系模式 他可以形式化地表示为：
  R（U,D,DOM,F）
  R为关系名，U为组成该关系的属性名集合，D为U中属性所来自的域，DOM为属性向域的映射集合，F为属性间数据的依赖关系集合

  由于D，DOM与模式设计关系不大，因此在实际运用的过程中把关系模式看作一个三元组：
  R<U,F>

• 第一范式 P178

  当且仅当U上的一个关系r满足F时，r称为关系模式R<U,F>的一个关系

  满足条件：关系满足每一个分量必须是不可分的数据项 的关系模式 为第一范式

• 数据依赖 P178

  数据依赖是一个关系内部属性与属性之间的约束关系。

  数据依赖包括 函数依赖 和 多值依赖

  函数依赖如： Sname=f(Sno) 表示 一旦学号Sno 被确定了，那么 姓名Sname也就被确定了
  记作 Sno->Sname

• 函数依赖

  R<U,F>
  X,Y是U的子集
  当X被决定了，Y就被唯一决定了时， 记作：X->Y

  为何这里X，Y是U的子集呢？ 有（Sno,Sname）-> Sclass
  这样情况的存在

• Y对X的完全函数依赖 P181

  记作方式看书
  即 X 中属性没有冗余，缺失了 其中任何属性都无法推出Y

  Y对X的部分函数依赖则相反，X中是有冗余的

  如（Sno,Sname）-> Sclass 是Sclass 对（Sno,Sname）的部分函数依赖，因为本来只要Sno->Sclass 就行了，现在多了个Sname

• 码 P181
  主码和候选码都有性质： K为R<U,F>的码，则U对K完全依赖

范式

• 2NF P182
  R<U,F> ,R∈1NF，且每一个非主属性完全依赖于任何一个候选码，则R<U,F>∈2NF
  消除非主属性对码的部分函数依赖

• 3NF P184
  R<U,F> ,R∈1NF，R中不存在码X，属性组Y，非主属性Z(Z不为Y的子集)，使得X->Y，Y->Z成立，X不依赖于Y，R<U,F>∈3NF

  效果相当于在2NF基础上，消除了非主属性对码的传递函数依赖

• BCNF P184
  R<U,F> ,R∈1N，若X->Y,且Y不是X的子集时，X必含有码，R<U,F>∈BCNF

  效果相当于在3NF基础上消除主属性对码的部分函数依赖和传递函数依赖

  解释一下由BCNF得到的结论：

  因为我们知道码K，U完全依赖于K，又我们任何属性集都是U的子集，所以可说任何属性集完全依赖于K

举例

---

现在有F={A->C,B->C,C->D,DE->C,CE->A},问当前是几范式？

• 先求码 key=BE

• 一眼没有任何一个表示式满足BCNF，所以不是

• 而且有BE的真子集->非主属性（B->C），所以2NF和3NF都不是

• 则为1NF

---

Fmin={C->T,HR->C,HT->R,CS->G,HS->R},问当前是第几范式？

• 先求码 key=HS

• 只有HS->R，满足BCNF，其余都不满足，所以不是BCNF

• 不存在HS的子集->非主属性；但是存在 HS->HR->R->C,即存在传递依赖

HS能够推到HR这个属性组，因为HS->R，HS->H。

• 所以为2NF

# 数据依赖的公理系统

• 逻辑蕴含
  R<U,F> ,任何一个关系r,若函数依赖X->Y都成立（上面我们说了，关系就是值，在二维表中每一行为一个关系), 则称 F逻辑蕴含X->F

Armstrong 公理系统 P190,191

• A1 自反律
  Y⊆X⊆U，则X->Y 为F所蕴含

  解释：首先X，Y⊆U是先前条件，因为Y⊆X，所以 X->Y是恒成立的，如（Sno,Sname）-> Sname ,X 即（Sno,Sname）都包含Sname了，能够推出Sname不是毫无疑问的吗？

• A2 增广律

  若X->Y为F所蕴含，且Z⊆U，则XZ->YZ为F所蕴含

• A3 传递律

  若X->Y及Y->Z为F所蕴含，则X->Z为F所蕴含

• 合并规则
  X->Y,X->Z,则X->YZ

• 伪传递规则
  X->Y,WY->Z,有XW->Z

• 分解规则
  X->Y,Z⊆Y,有X->Z

• 引理
  X->A1A2..An成立的充分必要条件是X->Ai成立（i=1,2,..,k）

闭包

X+ 属性集X关于函数依赖集F的闭包 定义为：

X+={A|X->A能够由F根据Armstrong公理推导出}

需要注意的是A是属性，可以理解为X+表示所有X可以决定的属性

From this blog<----

案例：

F={AD->E AC->E BC->G BD->A AB->G A->C}

AD的闭包：

• 首先准备一个空集合吧，就叫他为S了：
  S首先初始化为AD，即最开始S=

• 然后通过S中的元素不断地推导
  AD->E A->C 然后相当于S={ADEC}
  然后AC->E
  然后推导不了

• 最终S中集合元素为 ADCE

最小依赖集/最小覆盖 P193

若函数依赖集F满足一下条件，则称F为一个极小函数依赖集

• （1）F中任一函数依赖的右部仅含有一个属性

• （2）F中不存在这样的函数依赖X->A,使得F与F-{X-A}等价
  即 （2）我们是要去除掉冗余的依赖

• （3）F中不存在这样的函数依赖X->A,X有真子集Z使得 F-{X->A} ∪ {Z->A} 与 F等价
  即（3）我们是要去除掉 左部中冗余的元素

案例

R<U,F>
U={ABCDEG}
F={AD->E,AC->E,BC->G,BCD->AG,BD->A,AB->G,A->C}
求Fmin

• 首先我们将F的右边变成仅含有一个属性的样子

  AD->E
  AC->E
  BC->G
  BCD->A
  BCD->G
  BD->A
  AB->G
  A->C

• 然后我们去除冗余的依赖

  • 通过去除 右部相同，左部包含的依赖
    如 BC->G 和 BCD->G
    BD->A 和 BCD->A
    我们要去除掉 BCD->G , BCD->A
    于是留下
    AD->E
    AC->E
    BC->G
    BD->A
    AB->G
    A->C

  • 通过 “闭包” 判断依赖是否冗余
    这里的闭包有点特别，不是我们上面说的闭包
    如 AD->E 我们求AD的“闭包”，S初始化为{AD}，但是然后不能够通过AD->E 来将E加入到S
    因为我想看下这个E是否能够通过别的依赖推出，如果能够推出则说明AD->E是多余的
    最终：AD+={ADCE}，说明AD->E冗余 ，要删除

  AC+={AC}
  BC+={BC}
  BD+={BD}
  AB+={ABCG} AB->G要删除
  A+={A}

  于是留下：
  AC->E
  BC->G
  BD->A
  A->C

• 然后我们去掉左部冗余的元素

  如AC->E 但是 A->C，所以说明 AC->E中C是冗余的
  则为
  AC->E 要变成 A->E

最终结果Fmin={A->E
BC->G
BD->A
A->C}

求候选码

下面例题来源:

已知关系模型R<U,F>，其中U=(A,B,C,D,E,G)，F={AB-->C,CD-->E,E-->A.A-->G}，求R的候选码。

算法：

• 找出只在函数依赖左部出现的属性X，X肯定是任意一个候选码的成员。
  因为只在左边出现，所以少了它肯定推不出全集U。
  只在右部出现，肯定不属于任何一个候选码。则不考虑这个元素为候选码

  具体做法为拿出左边出现的全部属性(以上述例子为例)： A B C D E
  再拿出右边出现的全部属性：C E A G
  然后对比一下发现 B D 只在左边出现过， G只在右边出现过
  即候选码中一定包含BD，而不包含G
  剩下属性为ACE

• 看下已经求出的属性组合的闭包是否为U ，这里BD的闭包不为U，如果为U那不用再往下面接着求了，答案就是BD，否则
  从剩下的属性中选择，与已经求出的属性组合进行组合: BDA BDC BDE
  再进行求闭包，如果闭包是全集U，那么就是候选码。

结果：

只在左边出现的是B和D，所以确定了BD，只在右边出现的是G，所以排除G，剩下A，C，E。

先考虑一个的组合，ABD，BCD和BDE，三个的闭包都是全集U，所以三个都是候选码，算法结束。

模式的分解

下面算法的描述均来自博客<----

基本概念 P194,195

• 模式的分解是什么？ P194

  关系模式R<U,F>的一个分解是指
  p={R1<U1,F1>,R2<U2,F2>...,Rn<Un,Fn>},其中U= U1 U U2...U Un,且并没有Ui属于Uj,1<=i,j<=n,Fi是F在Ui上的投影

• 无损连接性是什么？P195

  表示分解后的各个Ri能够通过自然连接还原到分解之间的R状态

• 保持函数依赖性是什么? P195

  表示分解前的R中存在的函数依赖 在 分解后的各个Ri中，而没有缺失

判别一个分解的无损连接性 P197

一般题目会给我们一下信息：

关系模式R<U,F> 告知U={A1,A2...,An}和F中的内容； 然后告知R<U,F>的一个分解p={R1<U1,F1>,R2<U2,F2>....Rk<Uk,Fk>},然后要我们判断这个分解的无损连接性

• 首先将F化为最小依赖集

• 然后求出R<U,F>的候选码，其作用可以用来判断：最后出现a1a2..an的行对应的Ri<Ui,Fi>，其中Ui一定包含了候选码，没有包含则说明求错了

接下来我以例子讲解：

R<U,F>,U={ABCDE},F={A->C,B->C,C->D,DE->C,CE->A}
R<U,F>的一个分解为p={R1(AD),R2(AB),R3(BE),R4(CDE),R5(AE)}

• 上述F已经为最小依赖集了，而且码为BE

• 构建一张5行5列的表格，其中行表示p中的每一个R，列表示U中的每一个属性;
  如果列j中的属性Aj，出现在行i对应Ri的Ui中，那么这个这个格子中填入aj
  如果没出现，这个格子填入bij

  	A	B	C	D	E
  R1(AD)	a1	b12	b13	a4	b15
  R2(AB)	a1	a2	b23	b24	b25
  R3(BE)	b31	a2	b33	b34	a5
  R4(CDE)	b41	b42	a3	a4	a5
  R5(AE)	a1	b52	b53	b54	a5

  根据我们上面说的候选码的作用，我们可以提前猜测到 R3(BE)这一行是会出现a1a2..a5的行

• 接下来我们要用F={A->C,B->C,C->D,DE->C,CE->A}来不断更新上述表,结束状态有两种

  • 第一种状态是某行中出现了a1a2...a5这样的情况，则说明上述题目给出的分解是无损连接分解
  • 第二种状态是已经遍历完了全部F中的依赖式，表中一点变化也没有，则可以退出了，则说明上述题目给出的分解不是无损连接分解
    
    

• 具体更新规则为：

  拿出F中的一个函数依赖式，这里我就拿出A->C了
  然后看A这一列，找出其中有相同元素的行：这里第1,2,5行都是相同元素a1

  然后看C这一列，对应刚才我们找出的行（即第1,2,5行）,如果C这列这些行（即第1,2,5行）中出现过元素a,那么我们可以将C这列这些行（即第1,2,5行）全部改为a；
  举例：假设C列真的在第1,2,5行中的某一行出现了a3，则可将C列第1,2,5行全部改为a3

  如果如果C这列这些行（即第1,2,5行）中没有出现过元素a，我们将C这列这些行（即第1,2,5行）全部改为最小的b
  举例：就如题目中所示，C列第1,2,5行元素分别为b13,b23,b53, 那么最小的b就是b13了，然后将C列第1,2,5行元素全部改为b13

  然后不断用上述规则更新，直到到终结状态

  特殊点说明：有时候还可能遇到如DE->C，那么这个时候就是看DE这两列，找出DE列中有相同元素的行来，如果没有就算了，执行continue

• 考试的时候，一定要画出最后的表处理，当然如果试卷上还有空的话，最好画出初始的表来

  上述例子中最终的表为：

  	A	B	C	D	E
  R1(AD)	a1	b12	b13	a4	b15
  R2(AB)	a1	a2	b13	a4	b25
  R3(BE)	a1	a2	a3	a4	a5
  R4(CDE)	a1	b42	a3	a4	a5
  R5(AE)	a1	b52	a3	a4	a5

  可以看出果然是R3(BE)这行出现了a1a2..a5,答案就是 上述题目给出的分解是无损连接分解

3NF的保持函数依赖分解

算法1：分解为3NF,且保持依赖保持性。
算法输入：关系模式R<U,F>;
算法输出：R的一个分解ρ=(R1,R2…Rn),Ri为3NF，且ρ具有依赖保持性。

具体步骤如下：

• 对R<U,F>中的F进行极小化处理(处理后依然记为F)

• 找出不在F中出现的属性集合（记作U0），把这样的属性构成一个关系模式R0<U0,F0>。同时将U0中的属性从U中除去（剩余的属性集合依然记作U）

• 若有 X->A ∈ F，且XA=U，则p={R},算法终止。

• 对于F中的每一个Xi->Ai,都构成一个关系子模式Ri=XiAi;

• 停止分解，输出ρ；

举例：

设有关系模式R<U,F>，其中U={C,T,H,R,S,G},F={CS->G,C->T,TH->R,HR->C,HS->R},保持函数依赖分解为3NF。

• F已经为最小依赖集

• U中不存在元素在F中没出现过

• 不存在X->A,XA=U

• 对于F中的每一个Xi->Ai,都构成一个关系子模式，得到R1=CSG,R2=CT，R3=THR,R4=HRC,R5=HSR;

4. ρ= { R1,R2,R3,R4,R5 } ;

3NF的保持函数依赖和无损连接性

算法2：分解为3NF,使他既具有无损连接性，又具有依赖保持性；
输入：关系模式R，最小依赖集Fm;
输出：R的一个分解ρ=(R1,R2…Rn),Ri为3NF，具有无损连接性且ρ具有依赖保持性。

具体如下：

• 根据算法1得到具有的依赖保持性分解ρ；

• 求出R的候选码X,令ρ=ρ∪{X};

• 停止分解，输出ρ；

举例

R<U,F>
U={ABCDEF}
Fmin={C->E C->F F->B AC->D D->E}

• 首先我们进行算法1，使得变成3NF的保持函数依赖

  • 不存在 X->A 满足 XA=U

  • 左部全部元素为 C,F,A,D
    右部全部元素为 E,F,B,D
    即不存在某些属性与F中所有依赖的左部与右部都无关

  • R1<{CEF},{C->E,C->F}> 因为C->E C->F 具有相同的左部，所以可以合并
    R2<{FB},{F->B}>
    R3<{ACD},{AC->D}>
    R4<{DE},{D->E}>

  • p= { R1,R2,R3,R4

• 求出R的候选码X,令ρ=ρ∪{X};

  • 找出只在左部出现的元素，其一定为候选码中的元素
    根据Fmin={C->E C->F F->B AC->D D->E}，
    左部全部元素为 C,F,A,D
    右部全部元素为 E,F,B,D
    所以 C,A为候选码

  • 找出只在右部出现的元素，其一定不是候选码中的元素
    所以 E,B一定不是

  • 余下 F,D; 但是AC本身就可以推出U来，所以AC就是候选码

  • 让p=p∪{AC}, 即让p∪R5<{ACD},{AC->D}>
    但是p中已经有了R5<{ACD},{AC->D}>，所以最终

• p= {R1,R2,R3,R4

---

---

• 解释一：首先我们看到因为CE->A的U={ACE},然后A->C的U={AC},他们是一种包含关系，所以我们可以尝试能不能将CE->A和A->C放到一起。根据我们上面求码的方法，我们得到如果将CE->A和A->C放到一起，那么码上CE或AE。因为3NF的要求是：不存在非主属性对码的部分依赖以及不存在非主属性的传递依赖。这里CEA三个属性都是主属性，所以不存在上述问题，即符合3NF，所以能将CE->A和A->C放到一起。

• 解释二：同上

• 解释三: 记得写

---

转换为BCNF范式 P199

需要注意的是这个方法当给出关系模式R<U,F>时，并不要求我们得到极小依赖集F再进行求，直接用其给出的F求就行

• 首先我们将我们的答案p（即分解后得到的关系模型集合p={R1<U1,F1>,R2<U2,F2>...Rn<Un,Fn>}）,初始化为p=

• 然后要得到p中每一个关系模型Ri的码，因为我们要判断p中每一个关系模式是否为BCNF，如果全是，则算法终止，p就是答案;否则就还要继续
  根据BCNF的定义 R<U,F> ,R∈1N，若X->Y,且Y不是X的子集时，X必含有码，R<U,F>∈BCNF
  则对于每一个关系模式Ri,都看下函数依赖的左部是否都是码，如果都是，则这个关系模式Ri是BCNF；反之不是

• 对于不是BCNF的关系模式Ri<Ui,Fi>,我们从Fi选择出“影响最小”（这个含义将在下面举例再讲）的函数依赖（假设为A->a）,然后将形成新的关系模式Ri+1<{A},{A->a}>；
  然后原来的Fi要去除A->a这个函数依赖，Ui要去除a这个属性，变成新的关系模式R，然后p中就少了关系模式Ri,多了关系模式Ri+1和Ri

• 重复上述步骤，直到p中的关系模式都是BCNF

举例

上述步骤看起来很繁杂，我们在考试的时候可以每一次分出新的关系模式时，都保证其为BCNF，然后就可以不管他了，这样减少了工作。

同时考试时要求画出二叉分解树

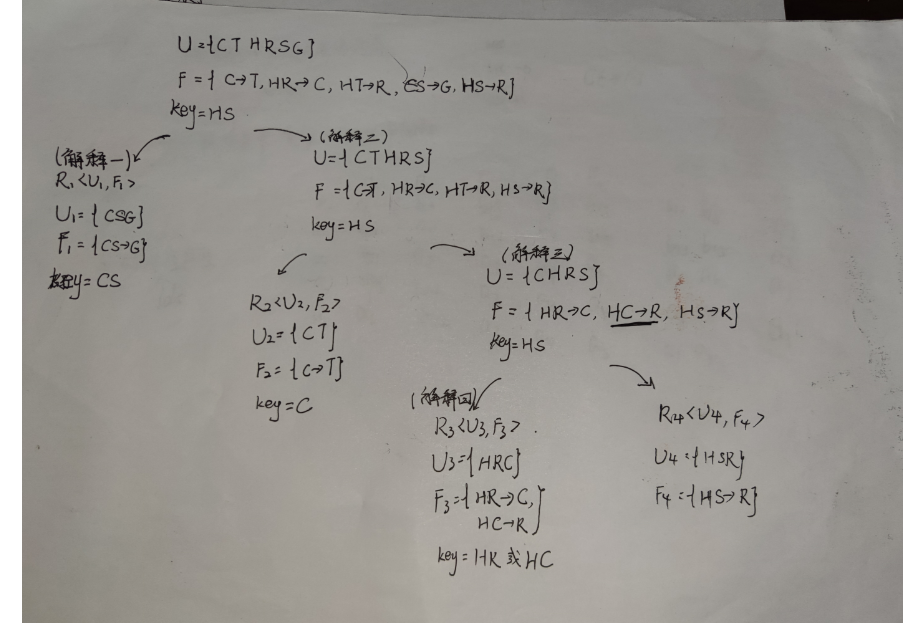
下面我会以例子：R<U,F>,U={CTHRSG},F={C->T,HR->C,HT->R,CS->G,HS->R}为例

• 解释一：可以观察到上述R并不是BCNF，则我们从F中拿出CS->G,形成新的关系模式R1。选择CS->G的原因是他“影响最小”，所谓影响最小是指从F中去除CS->G后，对于其他函数依赖影响个数，CS->G谁都不影响，因为F中的函数依赖左部都没有G；如果是去除HR->C后，那么C->T，CS->G会收到影响

• 解释二：可以看到这里的R<U,F>,U和F相比原来的U和F我们分别去除了G和CS->G
  R1已经是BCNF了，也就是说我们让他待到p就行了，以后可以不用管他，我们接下来只要考虑R

• 解释三： 注意这里的HC->R，以前是HT->R，因为我们分出了C->T,T已经被我们从U中去除了，又因为C->T，所以HT->R中的T被C代替了

• 解释四：需要注意的是，我们不一定每一次都只分一个出去，HR->C与HC->R，因为这两者的U都是{HRC}，这两者在放在一起，通过我们上面求码的方式可以得到码为HR或HC，那么F也符合BCNF的规则，所以这两者可以放到一起。

再来追加一问：分解为BCNF范式后，问函数依赖保不保持。

我们只要看下分析后得到的各个Fi,看下全部的Fi与最初还没分解的F相比是否一样

这里多了个HC->R，所以函数依赖并不保持！

---