AtCoder Beginner Contest 278

《F - Shiritori 》

博弈

 

 

 首先在这个博弈题中有个很重要的结论：

　　1.如果一个点，走一步，能够到达的点如果其中有一个为先手必胜点，那么这个点必然是先手必败点

　　2.如果一个点，走一步，能够到达的点如果全部为先手必败点，那么这个点必然是先手必胜点

这道题如果用爆搜的方式：

首先我们可以根据他的单词首尾相连的方式建个图，这个建图很有讲究，可以在O（n）的时间内建出

 

 

 即就是将开头为c的单词的下标i，保存在集合中，然后

在尾部为单词needc时，就去找头部为needc的单词

 

 

 注意这里的爆搜是要回溯的，因为全局的状态会根据搜索的起始点儿不同，比如：

 

 

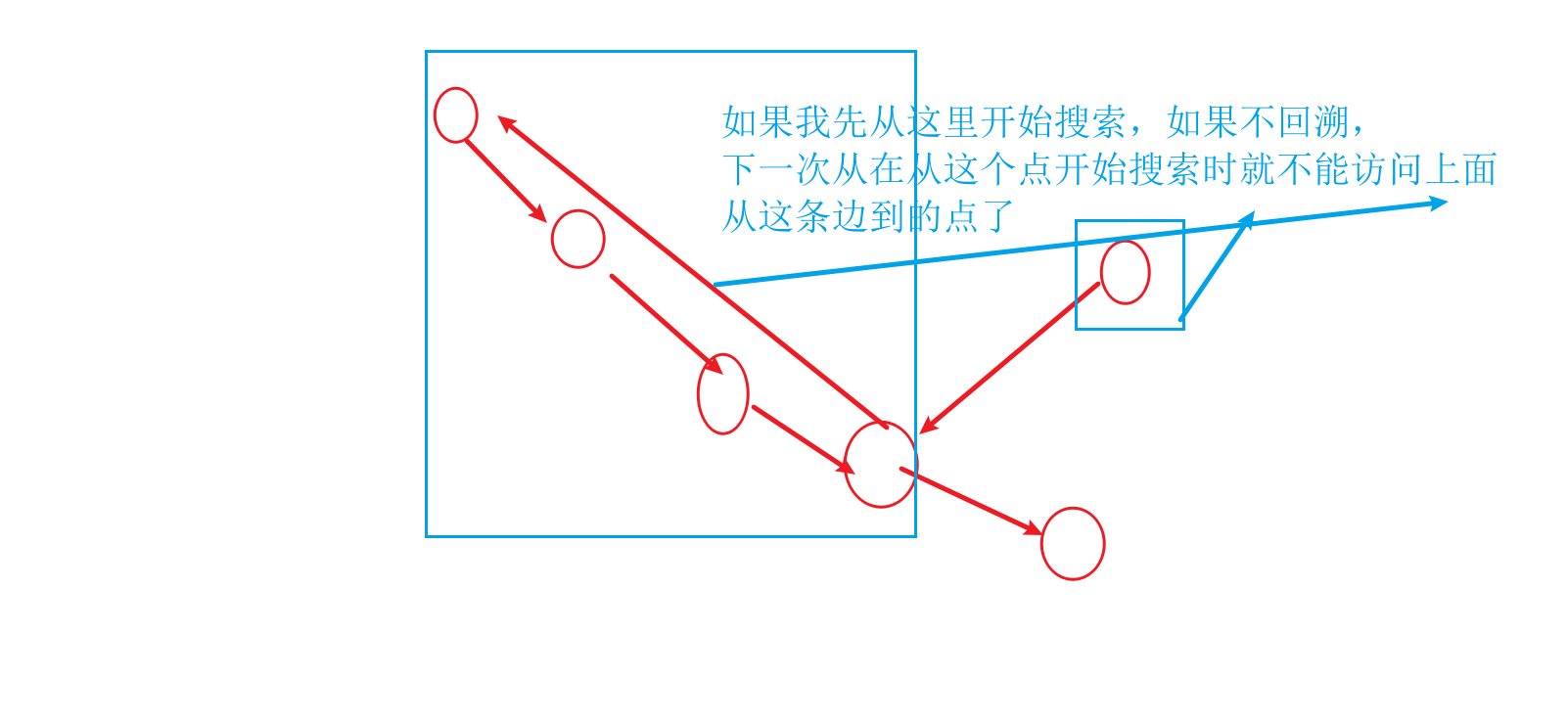
 于是：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
const int N = 20;
// dp[i]表示以第i个字符串为先手最终的结果
//-1表示最初始的状态，1表示先手必胜,0表示先手必败
int dp[N], n;
string str[N];
// sides[i]表示以字母i开头的字符有哪些
vector<int> sides[2 * N];
// dfs时有用
bool vis[N];
int dfs(int u)
{
    int needc = str[u].back() - 'a';
    for (int i = 0; i < sides[needc].size(); i++)
    {
        int to = sides[needc][i];
        if (!vis[to])
        {
            vis[to] = true;
            if (dfs(to))
            {
                vis[to] = false;
                return dp[u] = 0;
            }
            vis[to] = false;
        }
    }
    return dp[u] = 1;
}
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> str[i];
        int c = str[i][0] - 'a';
        sides[c].push_back(i);
    }
    for (int i = 1; i <= n; i++)
    {
        vis[i] = true;
        if (dfs(i))
        {
            cout << "First" << endl;
            return 0;
        }
        vis[i] = false;
    }
    cout << "Second" << endl;
    return 0;
}

然鹅会超时，按照状态压缩我还不理解：

 

 

 

 

 这里我有很多疑惑点:

1.这里枚举k，如果枚举的最后的一个单词，根本不存在怎么办？

比如状态1111011是枚举到的,但是枚举到的单词k根据不存在于任何上面的状态单词中怎么办？

  《AtCoder Beginner Contest 209 E - Shiritori 》

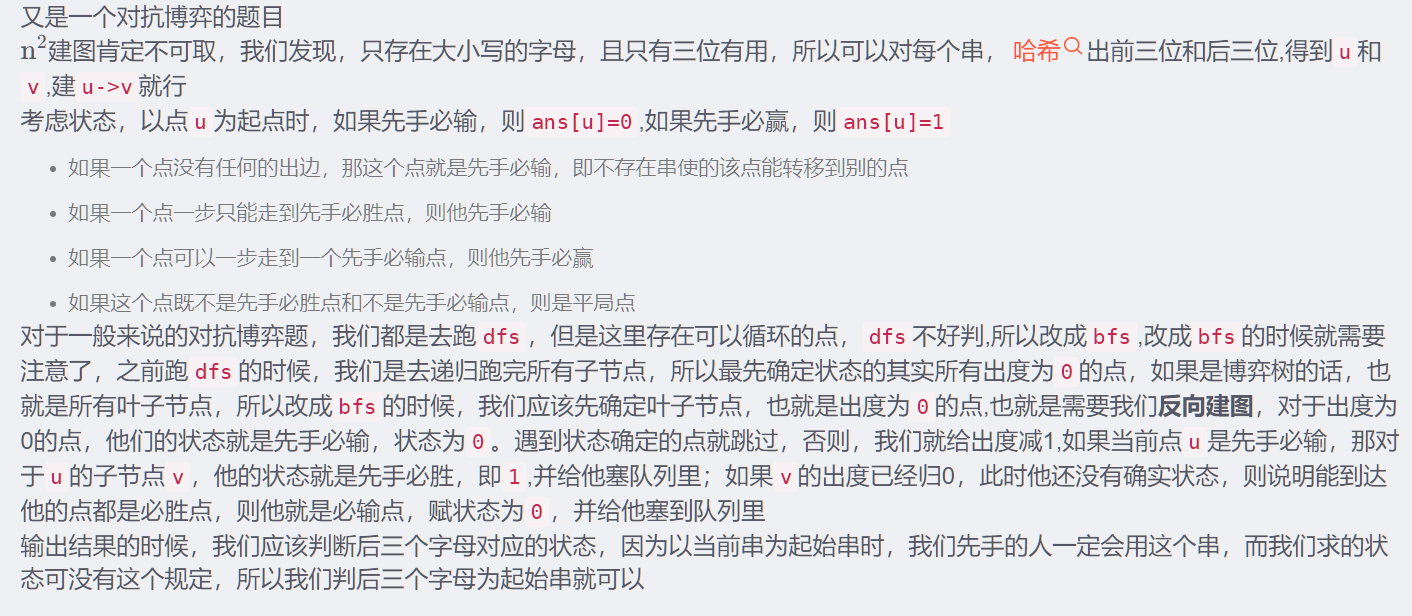
DAG(有向无环图)，拓扑排序，博弈

参考博客：https://blog.csdn.net/weixin_51216553/article/details/124272620

 

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
const int N = 200005;
// backstr[i]表示以数字i结尾的字符串有..
vector<int> sides[N], backstr[N];
string str[N];
int n, rd[N];
queue<int> q;
int get(string str)
{
    int num = 0;
    for (int i = 0; i < 3; i++)
    {
        if ('A' <= str[i] && str[i] <= 'Z')
            num += (str[i] - 'A' + 26);
        else if ('a' <= str[i] && str[i] <= 'z')
            num += (str[i] - 'a' + 0);
        num *= 52;
    }
    num /= 52;
    return num;
}
// ans[i]表示从第i个字符串开始的状态，如果为1表示必胜，-1表示必输，0表示平局
int ans[N];
void bfs()
{
    while (q.size())
    {
        int top = q.front();
        q.pop();
        /* cout << "top:" << top << endl; */
        int backnum = get(str[top].substr(0, 3));
        // 这里可以保证backstr[backnum].size()>0,因为如果其不大于0，那么这个top字符串就不会匹配到他了
        // 我这里看的是top字符串可以指向哪些字符串
        for (int i = 0; i < backstr[backnum].size(); i++)
        {
            int to = backstr[backnum][i];
            // 表示这个点的状态已经确定
            if (ans[to] != 0)
                continue;
            rd[to]--;
            // 表示存在一条可以让从to开始失败的路即to->top;
            // 即to是必败点
            //只要状态确定，就可以放到队列中更新状态
            if (ans[top] == 1)
            {
                ans[to] = -1;
                q.push(to);
            }
            // 表示到目前为为止周围的点都是必败点，同时rd[to]==0，表示把点都看过了
            else if (ans[top] == 0 && rd[to] == 0)
            {
                ans[to] = 1;
                q.push(to);
            }
        }
    }
}
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> str[i];
        sides[get(str[i].substr(0, 3))].push_back(i);
        backstr[get(str[i].substr(str[i].length() - 3, 3))].push_back(i);
    }
    for (int i = 1; i <= n; i++)
    {
        /*  cout << str[i].substr(str[i].length() - 3, 3) << endl; */
        string backstr = str[i].substr(str[i].length() - 3, 3);
        int num = get(backstr);
        /*  cout << num << endl; */
        rd[i] += sides[num].size();
        /*  cout<<rd[i]<<endl; */
        if (rd[i] == 0)
        {
            ans[i] = 1;
            q.push(i);
        }
    }
    bfs();
    for (int i = 1; i <= n; i++)
    {
        if (ans[i] == 0)
            cout << "Draw" << endl;
        else if (ans[i] == 1)
            cout << "Takahashi" << endl;
        else
            cout << "Aoki" << endl;
    }
    return 0;
}

但是这份代码是错误的。。。。。我完全不知道错在哪里