数论----质数

 《判断是否为质数》

 1 bool isPrime(int x)
 2 {
 3     if (x < 2)
 4         return false;
 5     for (int i = 2; i <= x / i; i++)
 6     {
 7         if (x % i == 0)
 8             return false;
 9     }
10     return true;
11 }
时间复杂度：O（sqrt(n)）;

《分解质因数》

 

 

 

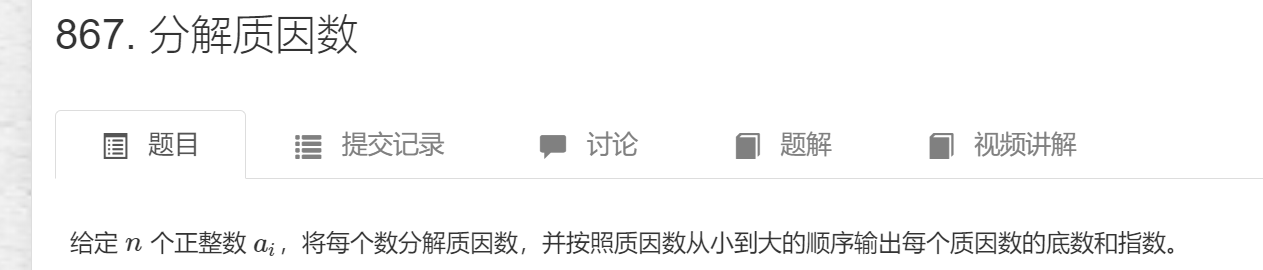
 1 void divide(int x)
 2 {
　　　　//所以这里可以优化成 x/i 
 3     for (int i = 2; i <= x / i; i++)
 4     {
　　　　　　　//这里不用担心i是合数而进入了if语句，能够进入if语句说明i一定是质数
　　　　　　　//因为合数可以被分解成质数相乘，然而这些质数早在x%i之前,就分解完了
 5         if (x % i == 0)
 6         {
 7             int s = 0;
 8             while (x % i == 0)
 9             {
10                 x /= i;
11                 s++;
12             }
13             cout << i << "^" << s << endl;
14         }
15     }
　　　　//注意：
16     if (x > 1)
17         cout << x << "^" << 1 << endl;
18     return;
19 }

 最好时间复杂度O（logn),最坏时间复杂度O（sqrt(n)）；

《筛质数》

 

 

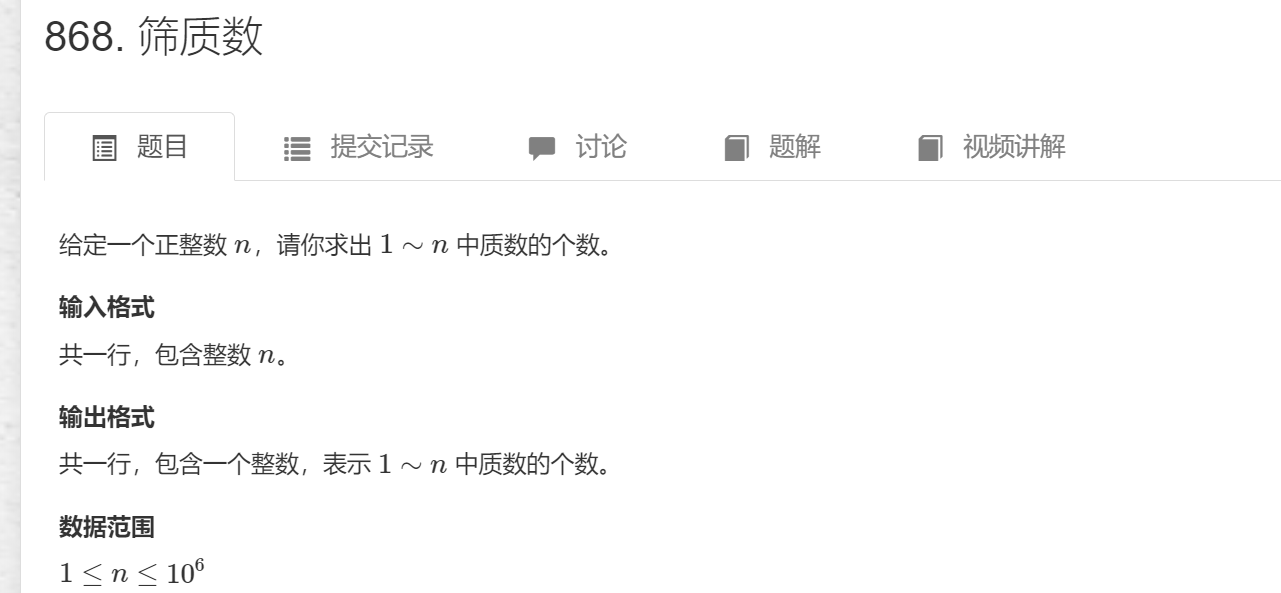
 这里介绍最常用的，时间复杂度为O（n）的写法：线性筛

其基本思想就是用最小质因子筛选出每一个合数，留下质数

 1 #include <iostream>
 2 #include <cstring>
 3 #include <algorithm>
 4 using namespace std;
 5 const int N = 1e6;
 6 int main()
 7 {
 8     int n;
 9     cin >> n;
10     int primes[N], cnt = 0;//primes是用来保存已经确定的质数
11     bool st[N];
12     for (int i = 2; i <= n; i++)
13     {
14         if (!st[i])
15             primes[cnt++] = i;
　　　　　　//对于一个数i，如果i%primes[j]==0,那么primes[j]一定是i的最小质因子（因为primes数组从小到大来装质数的）
　　　　　　//那么数i*primes[j]的最小质因子数i,所以st[primes[j]*i]=true;
　　　　　　//如果接下来不break，下次i*primes[j+1]这个数的最小质因子不一定是primes[j+1]，如i=4,primes[j]=2,primes[j+1]=3;
　　　　　　//如果i%primes[j]!=0,说明i与primes[j]互质，i*primes[j]就是个合数了,这个数是我们要筛选出的
　　　　　　//而且primes[j]一定是合数i*primes[j]的最小质因子
16         for (int j = 0; primes[j] <= n / i; j++)
17         {
18             st[primes[j] * i] = true;
19             if (i % primes[j] == 0)
20                 break;
21         }
22     }
23     cout << cnt;
24     return 0;
25 }

 《练习》

《素数距离》

原题链接：https://www.acwing.com/problem/content/description/198/

 

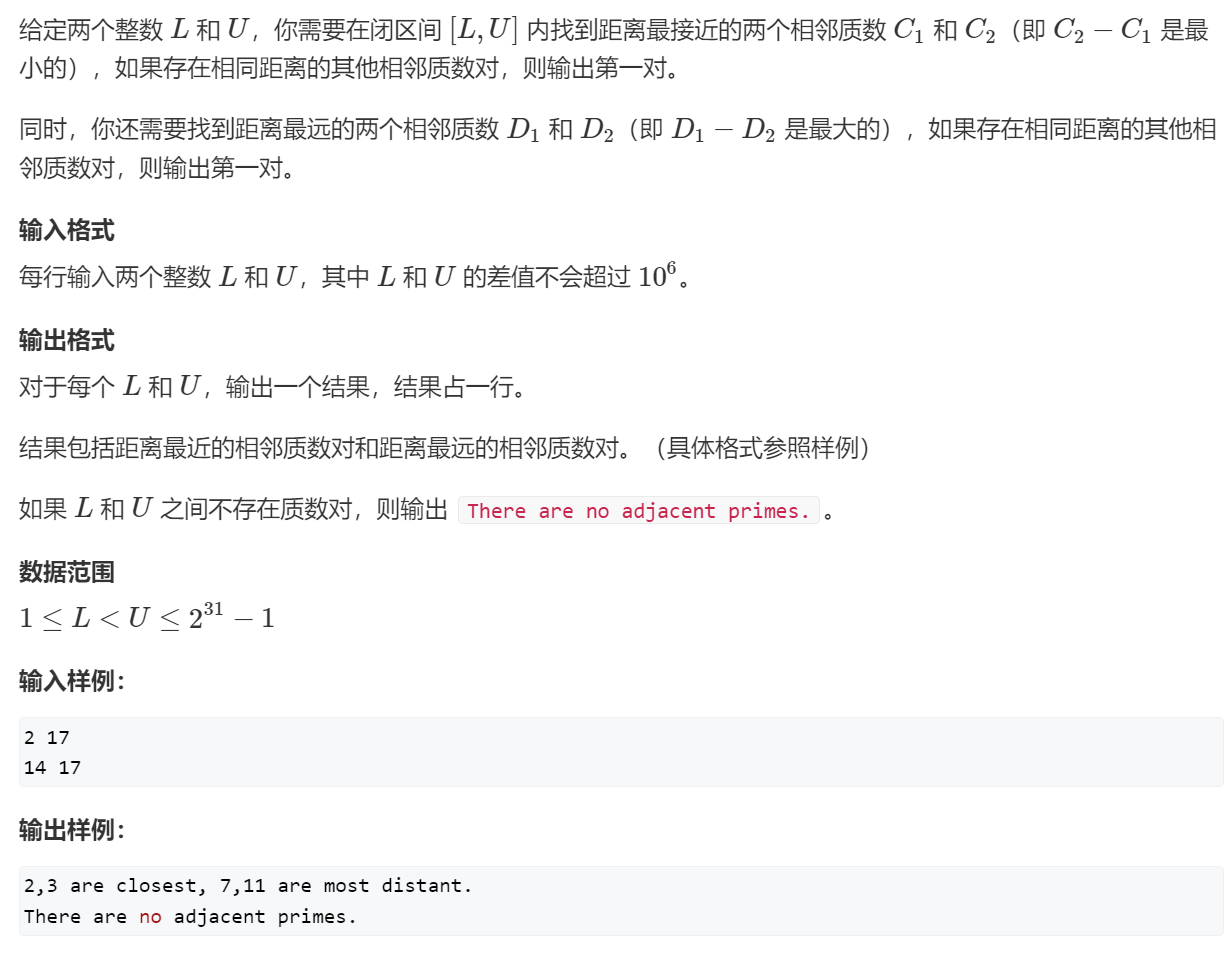
 一般情况下，直接一个线性筛就可以搞定问题，但是这里l<r<=2^31-1,即使是线性筛也会超时

这时就要注意到：一个合数n，一定有两个因子 d与d/n; 假设 d<d/n,那么一定有d<sqrt(n);

其中的因子一定包含质数

我们可以用将1~sqrt(2^31-1)中的质数全部求出来，然后用这些质数筛掉所给区间[l,r]中的合数，

因为[l,r]中任意一个数i,其全部的=<sqrt(i)的质因子，一定都被我先求出来了

具体怎么筛除呢？

　　枚举每一个我已经选出的质数

　　

　　对于这个质数p，首先，找到比l大而且是p的最小倍数p0（   (l+p-1)/p*p    ）然后在[l,r]的范围内筛选出因子是p0的数，然后p0+=p;

这里有个问题，l,r的范围很大，大到我不可能用一个st数组判断是否其中某个数是否被筛掉，怎么办？

可以用j-l，j是我现在正在判断的数，st[j-l]=true/fasle

　　每一个质数枚举完后，余下的数就是[l,r]中的质数了

　　在拿出来，遍历一遍即可

 1 #include <iostream>
 2 #include <cstring>
 3 #include <cstdio>
 4 
 5 using namespace std;
 6 
 7 typedef long long LL;
 8 
 9 //sqrt(2^31 - 1)
10 const int N = 1e6 + 10;
11 
12 bool st[N];
13 int primes[N], cnt;
14 
15 void get_primes(int n) {
16     memset(st, 0, sizeof st);
17     cnt = 0;
18     for (int i = 2; i <= n; ++ i) {
19         if (!st[i]) primes[cnt ++ ] = i;
20         for (int j = 0; primes[j] * i <= n; ++ j) {
21             st[primes[j] * i] = true;
22             if (i % primes[j] == 0) break;
23         }
24     }
25 }
26 
27 int main() {
28     int l, r;
29     while (~scanf("%d%d", &l, &r)) {
30         get_primes(50000);
31 
32         //把[l,r]区间内所有的合数用他们的最小质因子筛掉
33         memset(st, 0, sizeof st);
34         for (int i = 0; i < cnt; ++ i) {
35             LL p = primes[i];
36             for (LL j = max(2 * p, (l + p - 1) / p * p); j <= r; j += p)
37                 st[j - l] = true;
38         }
39 
40         //剩下的所有的都是素数了
41         cnt = 0;
42         for (int i = 0; i <= r - l; ++ i)
43             if (!st[i] && i + l > 1)
44                 primes[cnt ++ ] = i + l;
45 
46         if (cnt < 2) printf("There are no adjacent primes.\n");
47         else {
48             //计算间隔
49             int minp = 0, maxp = 0;
50             for (int i = 0; i + 1 < cnt; ++ i) {
51                 int d = primes[i + 1] - primes[i];
52                 if (d < primes[minp + 1] - primes[minp]) minp = i;
53                 if (d > primes[maxp + 1] - primes[maxp]) maxp = i;
54             }
55             printf("%d,%d are closest, %d,%d are most distant.\n", 
56             primes[minp], primes[minp + 1], 
57             primes[maxp], primes[maxp + 1]);
58         }
59     }
60     return 0;
61 }

 

posted @ 2022-08-03 16:20  次林梦叶  阅读(55)  评论(0)    收藏  举报