多项式乘法FFT与NTT
多项式乘法FFT与NTT
前言
所谓多项式乘法,就是给定两个\(n\)项多项式\(f(x)=a_0+a_1x+a_2x^2+\dots a_{n-1}x^{n-1}\)以及\(g(x)=b_0+b_1x+b_2x^2+\dots b_{n-1}x^{n-1}\),让你求出这两个多项式的乘积\((f*g)(x)=(a_0+a_1x+a_2x^2+\dots a_{n-1}x^{n-1})(b_0+b_1x+b_2x^2+\dots b_{n-1}x^{n-1})\),用乘法分配律展开之后可以看出,乘积\((f*g)(x)\)就等于\(\sum_{i=0}^n{\sum_{j=0}^{n}a_jb_{i-j}x^i}\)。暴力计算每一项的系数\(\sum_{i=0}^n\sum_{j=0}^{n}a_jb_{i-j}\)需要\(O(n^2)\)的复杂度,一般来讲是不太行的,需要优化。
因为代数基本定理,平面上的\(n\)个点就可以确定一个\(n\)次多项式,所以多项式还有一种表示方法,称为点值表示法,就是用\(f(x)\)上的\(n\)个点\((x_0,f(x_0)),(x_1,f(x_1)),\dots,(x_{n-1},f(x_{n-1}))\)来表示多项式\(f(x)\)。在点值表示法下,多项式乘法可以直接\(O(n)\)计算:\(f(x)\)乘以\(g(x)\)乘积的点值表示法就是\((x_0,f(x_0) \times g(x_0)),(x_1,f(x_1)\times g(x_1)),\dots ,(x_{n-1},f(x_{n-1})\times g(x_{n-1}))\),对应相乘就可以了。
现在我们的关键就在于如何完成“系数表示”和“点值表示”之间的互相转换。如果随便取值,比如说\(0,1,...,n-1\)这\(n\)个值,代入\(f(x)\)计算的话,复杂度又会是\(O(n^2)\),更不用说“点值表示”转“系数表示”还需要\(O(n^2)\)的拉格朗日插值或者\(O(n^3)\)的高斯消元。为了在\(O(n\log n)\)复杂度内快速完成“系数表示”和“点值表示”的转换,竞赛中出现了\(\text{FFT}\)和\(\text{NTT}\)两种算法。
快速傅里叶变换FFT
前置知识:复变函数(了解复数运算和初等复函数即可) 线性代数(了解逆矩阵和线性矩阵方程即可)
单位\(n\)次复根
由代数基本定理,复数域内\(x^n=1\)有\(n\)个解,我们记\(x=e^{i\theta}\),然后又已知\(e^{2k\pi i}=1\),可以解得\(x=e^{\frac{2k\pi}{n}i}\),\(k\)分别取\(0,1,\dots ,n-1\)就得到了这\(n\)个解。为了方便,我们记\(\omega_n=e^{\frac{2\pi}{n}i}\),然后就可以用\(\omega_n^0,\omega_n^1,\dots,\omega_n^k,\dots,\omega_n^{n-1}\)来表示这个方程的\(n\)个解,称为\(n\)次单位复根,其中\(\omega_n^k=e^{\frac{2k\pi}{n}i}\)。借用OIwiki上的一张图,可以看出这\(n\)个根是\(n\)等分单位圆的\(n\)个点:
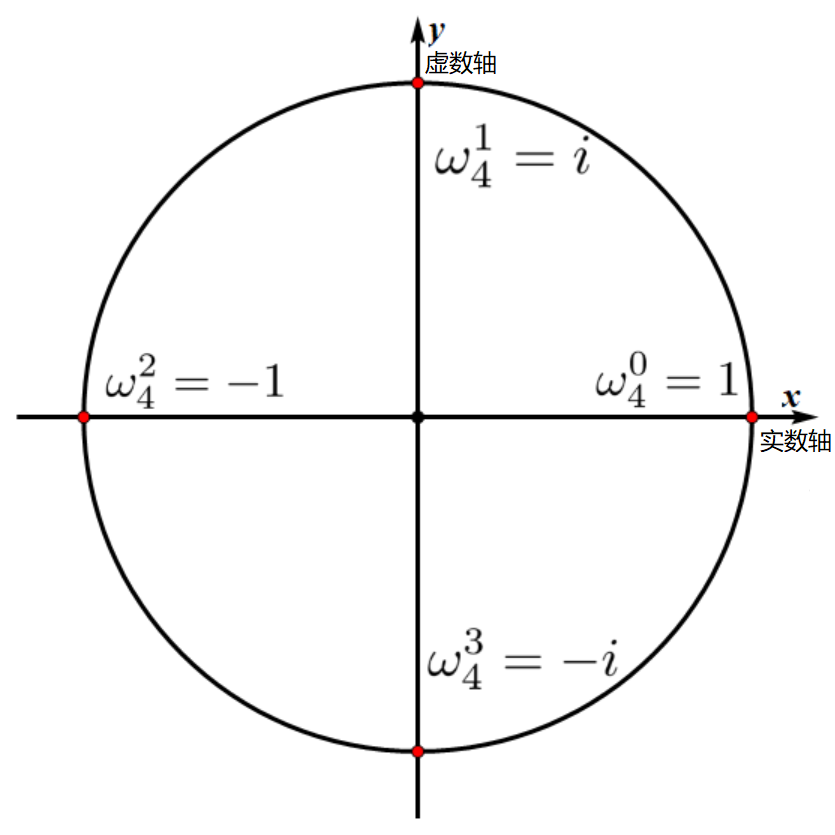
\(n\)次单位复根有两条非常美妙的性质:
折半引理:\(\omega_{2n}^{2k}=\omega_{n}^{k}\);证明非常简单,因为定义告诉我们\(\omega_n^k=e^{\frac{2k\pi}{n}i}\),所以\(\omega_{2n}^{2k}=e^{\frac{2(2k)\pi}{(2n)}i}=e^{\frac{2(k)\pi}{(n)}i}=\omega_{n}^{k}\),约分就完事了。
消去引理:\(\omega_{2n}^{k+n}=-\omega_{n}^{k}\),也可以由定义直接证:
除此以外你肯定还应该知道\(\omega_{n}^{k}=\omega_{n}^{k+n}\)以及\(\omega_{n}^{0}=1\),证明太简单就略过了。
离散傅里叶变换DFT
我们考虑多项式\(F(x)=a_0+a_1x+a_2x^2+\dots a_{n-1}x^{n-1}\),把下标按照奇偶分类,分成两个多项式:(假定\(n\)为偶数)
然后我们就发现,原先的\(F(x)=F_1(x^2)+xF_2(x^2)\)。此时我们把\(n\)次单位复根\(\omega_n^k\)代入,就会得到这样的结果,先看\(k<\frac{n}{2}\)的情况:
目前为止还没什么神奇的,但是如果比\(\frac{n}{2}\)大,神奇的事情就发生了。我们还是设\(k<\frac{n}{2}\),\((k+\frac{n}{2})\)表示比\(\frac{n}{2}\)更大的数,那么:
我们发现,\(F(\omega_{n}^{k+\frac{n}{2}})\)和\(F(\omega_{n}^{k})\)两个式子的区别仅仅只有一个“加号”和一个“减号”而已,也就是说,
只要把\(F_1(\omega_{\frac{n}{2}}^{0}),F_1(\omega_{\frac{n}{2}}^{1}),\dots,F_1(\omega_{\frac{n}{2}}^{k}),\dots,F_1(\omega_{\frac{n}{2}}^{\frac{n}{2}-1})\)这\(\frac{n}{2}\)个值算出来,
再把\(F_2(\omega_{\frac{n}{2}}^{0}),F_2(\omega_{\frac{n}{2}}^{1}),\dots,F_2(\omega_{\frac{n}{2}}^{k}),\dots,F_2(\omega_{\frac{n}{2}}^{\frac{n}{2}-1})\)这\(\frac{n}{2}\)个值算出来,
就可以用上面的两个公式算出所有的\(n\)个\(F(\omega_{n}^{k})\);而计算上面两串规模为\(\frac{n}{2}\)的数字又可以用递归,时间复杂度是\(O(n\log n)\)。
离散傅里叶逆变换IDFT
现在通过DFT我们把“系数表达式”转换成了“点值表达式”,但是完成乘法之后,我们还要想办法转回去。有人发现,这个过程可以完全和上面DFT的过程一模一样。
先说结论,把所有的\(\omega_{n}^{k}\)换成\(\omega_{n}^{-k}\),再用点值表达式跑一遍上面的DFT,得到的结果的实数部分,除以\(n\)就是系数表达式的结果了。下面给出的证明需要用到一点点线性代数的知识:
我们发现,其实离散傅里叶变换的过程可以理解为一个矩阵乘法。多项式\(F(x)=a_0+a_1x+a_2x^2+\dots a_{n-1}x^{n-1}\),把\(\omega_n^k\)代入,计算出的值记作\(f_k\),那么可以表示为
我们把左边那个矩阵记作\(X\),中间那个矩阵记作\(A\),等号右边那个记作\(Y\),得到矩阵方程\(XA=Y\)。而我们要求的一个矩阵\(B\),使得\(BY=A\),其实就是\(X\)的逆矩阵\(X^{-1}\)。结论是:
(其实就是把矩阵\(X\)里面的每个元素取倒数,或者说是把幂次变成原来的相反数,之后再除以\(n\)),证明这个玩意确实是逆矩阵,只要证明乘上\(X\)之后是单位矩阵\(E\)就行了。分类讨论:
①如果是在对角线上:\(X\)上的第\(k\)行是\(\omega_{n}^{0},\omega_{n}^{k},\omega_{n}^{2k},\dots,\omega_{n}^{k(n-1)}\),\(nX^{-1}\)的第\(k\)列是\(\omega_{n}^{-0},\omega_{n}^{-k},\omega_{n}^{-2k},\dots,\omega_{n}^{-k(n-1)}\),对应相乘就是
除以\(n\)之后就是\(1\);
②如果不是在对角线上:\(X\)上的第\(k_1\)行是\(\omega_{n}^{0},\omega_{n}^{k_1},\omega_{n}^{2k_1},\dots,\omega_{n}^{k_1(n-1)}\),\(nX^{-1}\)的第\(k_2\)列是\(\omega_{n}^{-0},\omega_{n}^{-k_2},\omega_{n}^{-2k_2},\dots,\omega_{n}^{-k_2(n-1)}\),对应相乘就是
令\(x=\omega_n^{k_1-k_2}\),这个东西就是个等比数列:
所以无论是除以\(n\)之前还是之后她都是\(0\);
乘积矩阵对角线上是\(1\),其他地方都是\(0\),那不就是单位矩阵\(E\)嘛。这样我们就完成了整个的证明。
递归版FFT
经历了上面的一系列操作和证明,其实我们已经可以写出递归版的\(\text{FFT}\)了。但是有一个小问题,就是我们在证明的时候都要求\(n\)是偶数,那\(n\)要不是偶数怎么办呢?
答案是没有办法(或者说办法很麻烦)。我们能做的只有在开始DFT之前,在多项式里面添加\(0\)使得\(n\)扩大到\(2\)的整数倍。比如说本来是\(5\)次多项式,我们就给他扩展到\(8\)项,只不过后面\(3\)项都是\(0\)。下面贴递归FFT的python代码:
from math import *
def dft(a: list, id = 1) -> list:
n = len(a)
if n == 1:
return a
k = n // 2
ans = []
a1 = []
a2 = []
for i in range(n):
if i % 2 == 0:
a1.append(a[i])
else:
a2.append(a[i])
a1 = dft(a1, id)
a2 = dft(a2, id)
for i in range(k):
angle = 2 * i * pi / n
x = cos(angle)
y = sin(angle) * id
ans.append(a1[i] + complex(x, y) * a2[i])
for i in range(k):
angle = 2 * i * pi / n
x = cos(angle)
y = sin(angle) * id
ans.append(a1[i] - complex(x, y) * a2[i])
return ans
def get_fx(a: list, x):
ans = 0
k = 1
for i in a:
ans = ans + i * k
k = k * x
return ans
def main():
a = list(map(int, input().split(' ')))
b = list(map(int, input().split(' ')))
n = 1
while n < len(a) + len(b):
n = n << 1
while len(a) < n:
a.append(0)
b.append(0)
print(a)
print(b)
a = dft(a)
b = dft(b)
ans = []
for i in range(n):
ans.append(a[i] * b[i])
print(ans)
ans = dft(ans, -1)
print(ans)
for i in range(n):
ans[i] = ans[i].real / n
print(ans)
if __name__ == '__main__':
main()
非递归版FFT
递归版FFT常数太大,如果你像我上面那样还用python写的话,那效率简直惨不忍睹。这玩意\(n=10000\)的时候都会有点卡,真的是让人怀疑自己是不是复杂度都写错了。
我们观察递归的“奇偶分组”这个过程,比如一开始是\(\{0,1,2,3,4,5,6,7\}\),第一次奇偶分组之后分成\(\{0,2,4,6\}\)和\(\{1,3,5,7\}\),第二次分组之后变成\(\{0,4\},\{2,6\},\{1,5\},\{3,7\}\);
观察序列\(0,4,2,6,1,5,3,7\),她们的二进制形式是\(000,100,010,110,001,101,011,111\)。可以发现这个序列其实就是把\(0,1,2,..,7\)二进制翻转之后的结果。
所以按照二进制翻转之后的顺序调整这个序列,然后不断把相邻两个合并,最终就能在\(O(n\log n)\)效率内完成非递归的\(\text{FFT}\)过程。这个操作成为蝴蝶操作。下面贴个\(\text{FFT}\)加速高精度乘法的完整代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
#define poi 1100100
#define inf 0x7fffffff
using namespace std;
typedef double db;
struct cpx {
db x, y;
cpx(db x = 0,db y = 0):x(x), y(y) {}
cpx operator + (cpx b) const{return cpx(x + b.x, y + b.y);}
cpx operator - (cpx b) const{return cpx(x - b.x, y - b.y);}
cpx operator * (cpx b) const{return cpx(x * b.x - y * b.y,x * b.y + y * b.x);}
}a[poi], b[poi];
int l, lim=1, r[poi], ans[poi];
inline int re() {
char x = getchar();
int k = 1, y = 0;
while(x < '0' || x > '9')
{if(x == '-') k = -1;x = getchar();}
while(x >= '0' && x <= '9')
{y = (y << 3) + (y << 1) + x - '0'; x = getchar();}
return y * k;
}
inline void wr(int x) {
if(x < 0) putchar('-'), x = -x;
if(x > 9) wr(x / 10);
putchar(x % 10 + '0');
}
void fft(cpx *a,int tp) {
for(int i = 0;i < lim; i++)
if(i < r[i]) swap(a[i], a[r[i]]);
for(int mid = 1;mid < lim; mid <<= 1) {
cpx bas(cos(M_PI / mid), tp * sin(M_PI / mid));
for(int i = mid << 1, j = 0; j < lim;j += i) {
cpx w(1, 0);
for(int k = 0; k < mid; k++, w = w * bas) {
cpx x = a[j + k], y = w * a[j + mid + k];
a[j + k] = x + y;
a[j + mid + k] = x - y;
}
}
}
}
signed main() {
int n = re() - 1;
for(int i = n; ~i; i--) {
char c = getchar();
while(c < '0'|| c > '9') c = getchar();
a[i].x = c-'0';
}
for(int i = n; ~i; i--) {
char c = getchar();
while(c < '0' || c > '9') c = getchar();
b[i].x = c - '0';
}
while(lim <= (n << 1)) lim <<= 1, l++;
for(int i = 0; i < lim; i++)
r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
fft(a, 1), fft(b, 1);
for(int i = 0; i <= lim; i++)
a[i] = a[i] * b[i];
fft(a, -1);
for(int i = 0; i <= lim; i++) {
ans[i] += (int)(a[i].x / lim + 0.5);
if(ans[i] >= 10) ans[i + 1] += ans[i] / 10, ans[i] %= 10, lim += (i == lim);
}
while((!ans[lim]) && lim >= 1) lim--;
for(int i = lim; ~i; i--) wr(ans[i]);
return 0;
}
快速数论变换NTT
FFT需要复数,还全是double,精度比较容易出问题,效率也比较差,还不能取模。如果是要用多项式来解决排列组合问题,FFT很多时候会无能为力。而基于数论的\(\text{NTT}\)就可以全是整数运算,而且还可以把结果取模,特别适合竞赛的环境。往往我们用多项式,说“多项式乘法”的时候,指的都是\(\text{NTT}\)。
原根
考虑一下这个方程的解\(x\),其中\(p\)是质数,\(\gcd(a,p)=1\):
用我们最熟悉的费马小定理一眼可以看出,\(x=p-1\)(当然\((p-1)\)的整数倍也可以,但与我们考虑的话题无关)。但是\(x=p-1\)可能不是最小的一个解,比如方程
\(x=6\)当然是方程的一个解,但是实际上最小的解是\(x=3\),因为\(2^3=8 \equiv 1 \pmod 7\)。那么我们就要考虑,什么时候\(x=p-1\)确实是方程\(a^x \equiv1 \pmod p\)的最小解呢?这就引出原根的定义:给定一个质数\(p\),如果正整数\(a\),满足\(a<p\),且使得\(a^x \equiv1 \pmod p\)的最小解是\(x=p-1\),那么称\(a\)是质数\(p\)的原根。
举例:比如说\(3\)是\(7\)的原根,因为\(3^1 \equiv 3 \pmod 7\),\(3^2 \equiv 2 \pmod 7\),\(3^3 \equiv 6 \pmod 7\),\(3^4 \equiv 4 \pmod 7\),\(3^5 \equiv 5 \pmod 7\),\(3^6 \equiv 1 \pmod 7\),可以看到最小的解确实是\(x=6\),而且当\(x\leq6\)时,每个\(3^x \mod 7\)的值都互不相同。
使用原根替代\(n\)次单位复根实现NTT
设\(g\)是质数\(p\)的原根,而且质数\(p=tn+1\)。那么原根的定义告诉我们,\(g^{tn}\equiv1 \pmod p\),而且除了\(x=tn\)之外,任何一个\(g^x\)对\(p\)取模的结果都不等于\(1\)。这样也可以得出,如果\(x\leq p-1\),那么每个\(g^x\)的值都互不相同。
所以我们设\(w_n=g^t\),那么我们可以得到\(n\)个互不相同的数字\(w_n^0,w_n^1,\dots,w_n^{n-1}\),其中第\((k+1)\)个数字\(w_n^k=(g^t)^k=g^{tk}\)。因为上面说过\(t=\frac{p-1}{n}\),所以\(w_n^k=g^{\frac{p-1}{n}k}\)。这个形式是不是有点似曾相识?\(\text{FFT}\)里面,\(\omega_n^k=e^{2\pi i \frac{k}{n}}\),而这里,\(w_n^k=g^{(p-1)\frac{k}{n}}\):也就是说,在\(\text{NTT}\)里,我们用\(g^{p-1}\)替代掉了原来的那个\(e^{2\pi i}\)。
我们还记得,\(\text{FFT}\)里面我们能搞那些操作,最重要的就是“折半引理”、“消去引理”两个性质。而现在我们发现:
折半引理:\(w_{2n}^{2k}=g^{\frac{(p-1)}{2n}(2k)}=g^{\frac{p-1}{n}k}=w_n^k\),约分完事。
消去引理:\(w_{2n}^{k+n}=w_{2n}^kw_{2n}^n=w_{2n}^kg^{(p-1)\frac{n}{2n}}=w_{2n}^kg^{\frac{p-1}{2}}\),并且我们知道,\((g^{\frac{p-1}{2}})^2=g^{p-1}=1\),但是\(g^{\frac{p-1}{2}}\)又不可能等于\(1\),所以一定有\(g^{\frac{p-1}{2}}=-1\),代回就得到\(w_{2n}^{k+n}=w_{2n}^kg^{\frac{p-1}{2}}=-w_{2n}^k\),这样就把消去引理证明了。
有了这两条引理,我们之前关于\(\text{FFT}\)的所有推导都可以成立。比如奇偶分组之后\(F(x)=F_1(x^2)+xF_2(x^2)\),\(k<\frac{n}{2}\)时代入\(x=w_n^k\)得到\(F(w_n^k)=F_1(w_{\frac{n}{2}}^k)+w_n^kF_2(w_{\frac{n}{2}}^k)\),代入\(x=w_n^{k+\frac{n}{2}}\)得到\(F(w_n^{k+\frac{n}{2}})=F_1(w_{\frac{n}{2}}^k)-w_n^kF_2(w_{\frac{n}{2}}^k)\)。这个结论使得我们能够用递归的方式处理离散傅里叶变换DFT。
也是同理,离散傅里叶逆变换IDFT的过程就是用\(w_n^{-k}\)代替\(w_n^k\)跑一遍DFT,跑完之后除以\(n\)就可以了。具体来讲,因为是在取模意义下,所以刚才的那个\(w_n^{-k}\)其实就是\(w_n^k\)在\(\mod p\)意义下的逆元;除以\(n\)其实也就是乘\(n\)在模\(p\)意义下的逆元。
最后还有一个小问题,就是我们要求质数\(p=tn+1\),也就是说\(n\)能整除\(p-1\)。我们只知道,在FFT之前我们会把\(n\)扩大到\(2\)的整数次幂,那NTT里面又如何来保证\(n|(p-1)\)这个性质呢?一般来讲,我们会选取的质数是\(p=998244353\),这个质数的原根是\(3\),而且还满足\(p-1=998244352=7\times 17\times 2^{23}\),所以我们只要让\(n\)扩大成\(2\)的整数次幂,那么就一定有\(n\)整除\((p-1)\)(因为我们扩展之后的\(n\)也不可能超过\(2^{23}\),\(2^{23}\)大概等于八百万)。
如果题目非要塞给你一个毫无特点的模数\(p\),那就只能使用任意模数\(\text{NTT}\),而这又是另一个故事了。
最后上一份\(\text{NTT}\)的完整代码
#include<bits/stdc++.h>
#define poi 2100000
using namespace std;
typedef long long ll;
const int mod=998244353,yg=3;//模数 998244353,原根为3
int a[poi],b[poi],lim=1,l,r[poi];
inline int re() {
char x = getchar();
int k = 1, y = 0;
while(x < '0' || x > '9')
{if(x == '-') k = -1;x = getchar();}
while(x >= '0' && x <= '9')
{y = (y << 3) + (y << 1) + x - '0'; x = getchar();}
return y * k;
}
inline void wr(int x) {
if(x < 0) putchar('-'), x = -x;
if(x > 9) wr(x / 10);
putchar(x % 10 + '0');
}
inline int ksm(int x,int y) {
int ans = 1;
for(; y; y >>= 1)
{
if(y & 1) ans = (ll)((ll)ans * x) % mod;
x = (ll)((ll)x * x) % mod;
}
return ans;
}
void ntt(int *a, bool tp)
{
for(int i = 0; i < lim; i++)
if(i < r[i]) swap(a[i], a[r[i]]);
for(int mid = 1; mid < lim; mid <<= 1)
{
int bas = ksm(tp ? yg : 332748118, (mod - 1) / (mid << 1));
for(int i = mid << 1, j = 0; j < lim; j += i)
{
int w = 1;
for(int k = 0; k < mid; k++, w = ((ll)w * bas) % mod)
{
int x = a[k + j], y = (ll)w * (ll)a[k + j + mid] % (ll)mod;
a[k + j] = (x + y) % mod;
a[k + mid + j] = (x - y + mod) % mod;
}
}
}
}
signed main() {
int n = re(), m = re();
for(int i = 0; i <= n; i++) a[i] = (re() + mod) % mod;
for(int i = 0; i <= m; i++) b[i]= (re() + mod) % mod;
while(lim <= n + m) lim <<= 1, l++;
for(int i = 0; i < lim; i++)
r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
ntt(a, 1), ntt(b, 1);
for(int i = 0; i < lim; i++) a[i] = ((ll)a[i] * b[i]) % mod;
ntt(a, 0);
int niyuan = ksm(lim, mod-2);
for(int i = 0;i <= n + m; i++)
wr(((ll)a[i] * niyuan) % mod), putchar(' ');
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号