排序算法

常见的大O表示形式

 

 

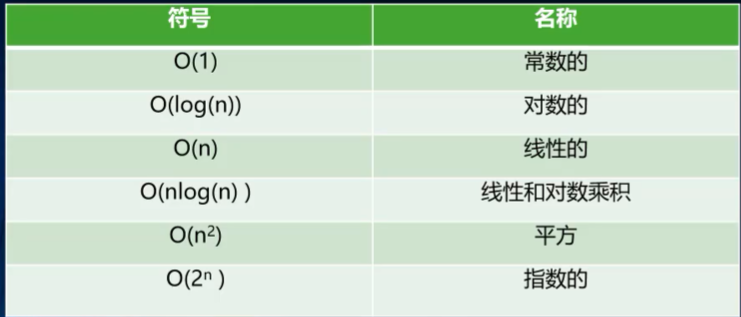
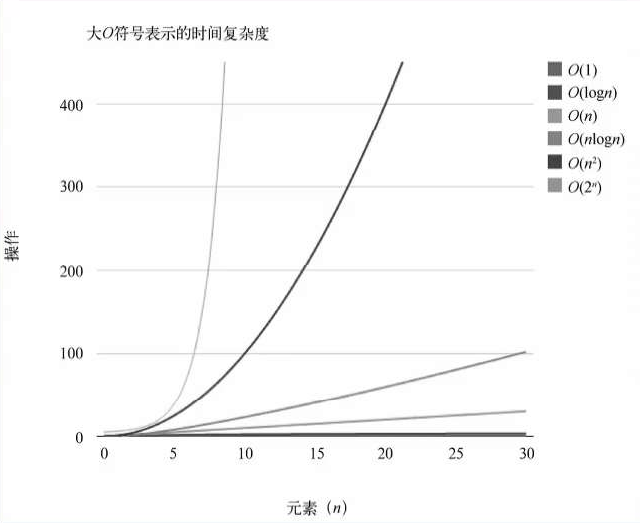
 可以看到效率从大到小分别是：O（1）> O（logn）> O（n）> O（nlog(n)）> O（n²）> O（2^n^）

 

推导大O表示法的三条规则：

• 规则一：用常量1取代运行时间中所有的加法常量。如7 + 8 = 15，用1表示运算结果15，大O表示法表示为O（1）；
• 规则二：运算中只保留最高阶项。如N^3 + 3n +1，大O表示法表示为：O（N^3^）;
• 规则三：若最高阶项的常数不为1，可将其省略。如4N^2^，大O表示法表示为：O（N^2^）;

 排序算法

1. 冒泡排序
2. 选择排序
3. 插入排序
4. 归并排序
5. 希尔排序
6. 快速排序
7. 堆排序
8. 桶排序

• 简单排序：冒泡排序、选择排序、插入排序；
• 高级排序：希尔排序、快速排序；

冒泡排序

冒泡排序的思路：

• 对未排序的各元素从头到尾依次比较相邻的两个元素大小关系；
• 如果左边的人员高，则将两人交换位置。比如1比2矮，不交换位置；
• 向右移动一位，继续比较2和3，最后比较 length - 1 和 length - 2这两个数据；
• 当到达最右端时，最高的人一定被放在了最右边；
• 按照这个思路，从最左端重新开始时，只需要走到倒数第二个位置即可；

 

实现思路：

两层循环：

• 外层循环控制冒泡趟数：

  • 第一次：j = length - 1，比较到倒数第一个位置 ；
  • 第二次：j = length - 2，比较到倒数第二个位置 ；

• 内层循环控制每趟比较的次数：

  • 第一次比较： i = 0，比较 0 和 1 位置的两个数据；
  • 最后一次比较：i = length - 2,比较length - 2和 length - 1两个数据；

详细过程如下图所示：

 

动态过程：

代码实现：

 // 冒泡排序
  ArrayList.prototype.bubblesort = function() {
    // 1 获取数组长度
    let length = this.array.length;
    //外层循环控制冒泡趟数
    for(let i = length - 1; i >= 0 ; i--) {
      //内层循环控制每趟比较的次数
      for (let j = 0; j < i; j++) {
        if(this.array[j] > this.array[j+1]) {
          // 交换两个数据
          this.swap(j, j+1);
        }
      }
    }
  }

冒泡排序的效率：

• 上面所讲的对于7个数据项，比较次数为：6 + 5 + 4 + 3 + 2 + 1;
• 对于N个数据项，比较次数为：(N - 1) + (N - 2) + (N - 3) + ... + 1 = N * (N - 1) / 2；如果两次比较交换一次，那么交换次数为：N * (N - 1) / 4；
• 使用大O表示法表示比较次数和交换次数分别为：O（ N * (N - 1) / 2）和O（ N * (N - 1) / 4），根据大O表示法的三条规则都化简为：O（N^2）;

选择排序

选择排序改进了冒泡排序：

• 将交换次数由O（N^2）减小到O（N）；
• 但是比较次数依然是O（N^2）；

选择排序的思路：

• 选定第一个索引的位置比如1，然后依次和后面的元素依次进行比较；
• 如果后面的元素，小于索引1位置的元素，则交换位置到索引1处；
• 经过一轮的比较之后，可以确定一开始指定的索引1位置的元素是最小的；
• 随后使用同样的方法除索引1意外逐个比较剩下的元素即可；
• 可以看出选择排序，第一轮会选出最小值，第二轮会选出第二小的值，直到完成排序。

实现思路：

两层循环：

• 外层循环控制指定的索引：

  • 第一次：j = 0，指定第一个元素 ；
  • 最后一次：j = length - 1，指定最后一个元素 ；

• 内层循环负责将指定索引（i）的元素与剩下（i - 1）的元素进行比较；

动态过程：

代码实现：

 // 选择排序
  ArrayList.prototype.selectionSort = function() {
    // 1 获取数组长度
    let length = this.array.length;
    // 2.外层循环,从0开始获取元素
    for(let i = 0; i < length -1 ; i++) {
      let min = i;
      //内层循环：从i+1位置开始，和后面的元素进行比较
      for (let j = min + 1; j < length; j++) {
        if(this.array[min] > this.array[j]) {
          // min变成更小的值的下标
          min = j;
        }
      }
      // 找到最小的值,交换位置
      this.swap(min, i);
    }
  }

选择排序的效率：

• 选择排序的比较次数为：N * (N - 1) / 2，用大O表示法表示为：O（N^2）;
• 选择排序的交换次数为：(N - 1) / 2，用大O表示法表示为：O（N）;
• 所以选择排序的效率高于冒泡排序；

插入排序

插入排序是简单排序中效率最高的一种排序。

插入排序的思路：

• 插入排序思想的核心是局部有序。如图所示，X左边的人称为局部有序；
• 首先指定一数据X（从第一个数据开始），并将数据X的左边变成局部有序状态；
• 随后将X右移一位，再次达到局部有序之后，继续右移一位，重复前面的操作直至X移至最后一个元素。

 

插入排序的详细过程：

 

动态过程：

代码实现：

// 插入排序
  ArrayList.prototype.insertionSort = function() {
    // 1. 获取数据长度
    let length = this.array.length;

    // 2.外层循环:从第一个位置开始获取数据,向前面局部有序进行插入
    for (let i = 1; i < length; i++) {
      // 内层循环：获取i位置的元素，使用while循环(重点)与左边的局部有序数据依次进行比较
      let temp = this.array[i];
      let j = i;
      while(this.array[j -1] > temp && j > 0) {
        this.array[j] = this.array[j -1];
        j --;
      }
      // while循环结束后，index = j左边的数据变为局部有序且array[j]最大。此时将array[j]重置为排序前的数据array[i]，方便下一次for循环
      this.array[j] = temp;
    }
  }

插入排序的效率：

• 比较次数：第一趟时，需要的最大次数为1；第二次最大为2；以此类推，最后一趟最大为N-1；所以，插入排序的总比较次数为N * (N - 1) / 2；但是，实际上每趟发现插入点之前，平均只有全体数据项的一半需要进行比较，所以比较次数为：N * (N - 1) / 4；

• 交换次数：指定第一个数据为X时交换0次，指定第二个数据为X最多需要交换1次，以此类推，指定第N个数据为X时最多需要交换N - 1次，所以一共需要交换N * (N - 1) / 2次，平局次数为N * (N - 1) / 2；

• 虽然用大O表示法表示插入排序的效率也是O（N^2），但是插入排序整体操作次数更少，因此，在简单排序中，插入排序效率最高；

希尔排序

 希尔排序是插入排序的一种高效的改进版，效率比插入排序要高。

希尔排序的历史背景：

• 希尔排序按其设计者希尔（Donald Shell）的名字命名，该算法由1959年公布；
• 希尔算法首次突破了计算机界一直认为的算法的时间复杂度都是O（N^2）的大关，为了纪念该算法里程碑式的意义，用Shell来命名该算法；

插入排序的问题：

• 假设一个很小的数据项在很靠近右端的位置上，这里本应该是较大的数据项的位置；
• 将这个小数据项移动到左边的正确位置，所有的中间数据项都必须向右移动一位，这样效率非常低；
• 如果通过某种方式，不需要一个个移动所有中间的数据项，就能把较小的数据项移到左边，那么这个算法的执行速度就会有很大的改进。

希尔排序的实现思路：

• 希尔排序主要通过对数据进行分组实现快速排序；
• 根据设定的增量（gap）将数据分为gap个组（组数等于gap），再在每个分组中进行局部排序；

假如有数组有10个数据，第1个数据为黑色，增量为5。那么第二个为黑色的数据index=5，第3个数据为黑色的数据index = 10（不存在）。所以黑色的数据每组只有2个，10 / 2 = 5一共可分5组，即组数等于增量gap。

• 排序之后，减小增量，继续分组，再次进行局部排序，直到增量gap=1为止。随后只需进行微调就可完成数组的排序；

具体过程如下：

• 排序之前的，储存10个数据的原始数组为：

• 设初始增量gap = length / 2 = 5，即数组被分为了5组，如图所示分别为：[8, 3]、[9, 5]、[1, 4]、[7, 6]、[2, 0]：

• 随后分别在每组中对数据进行局部排序，5组的顺序如图所示，变为：[3, 8]、[5, 9]、[1, 4]、[6, 7]、[0, 2]：

• 然后缩小增量gap = 5 / 2 = 2，即数组被分为了2组，如图所示分别为：[3，1，0，9，7]、[5，6，8，4，2]：

• 随后分别在每组中对数据进行局部排序，两组的顺序如图所示，变为：[0，1，3，7，9]、[2，4，5，6，8]：

• 然后然后缩小增量gap = 2 / 1 = 1，即数组被分为了1组，如图所示为：[0，2，1，4，3，5，7，6，9，8]：

• 最后只需要对该组数据进行插入排序即可完成整个数组的排序：

动态过程：

图中d表示增量gap。

增量的选择：

• 原稿中希尔建议的初始间距为N / 2，比如对于N = 100的数组，增量序列为：50，25，12，6，3，1，可以发现不能整除时向下取整。
• Hibbard增量序列：增量序列算法为：2^k - 1，即1，3，5，7... ...等；这种情况的最坏复杂度为O（N^3/2）,平均复杂度为O（N^5/4）但未被证明；
• Sedgewcik增量序列：

以下代码实现中采用希尔排序原稿中建议的增量即N / 2 。

 

这里解释一下上述代码中的三层循环：

• 第一层循环：while循环，控制gap递减到1；
• 第二层循环：分别取出根据g增量gap分成的gap组数据：将index = gap的数据作为选中的第一个数据，如下图所示，gap=5，则index1 = gap的数据为3，index2 = index1 -  gap = 0的数据为8，两个数据为一组。随后gap不断加1右移，直到gap < length，此时实现了将数组分为5组。

 

• 第三层循环：对每一组数据进行插入排序；

代码实现：

// 希尔排序
  ArrayList.prototype.shellSort = function() {
     //1.获取数组的长度
     let length = this.array.length
    //  2.获取初始增量(gap -> 间隔/间隙)
    let gap = Math.floor(length / 2);

    // 3.第一层循环：while循环(使gap不断减小)
    while (gap >= 1) {
      // 4. 第二层循环：以gap为增量，进行分组，对分组进行插入排序
      for (let i = gap; i < length; i++) {
        let temp  = this.array[i];
        var j = i;
        //5.第三层循环:寻找正确的插入位置
        while (this.array[j - gap] > temp && j > gap - 1) {
          this.array[j] = this.array[j - gap];
          j -= gap;
        }
      // 6. 将j位置的元素赋值temp
      this.array[j] = temp;
      }
      // gap减小
      gap = Math.floor(gap / 2);
    }
  }

 

快速排序

快速排序的介绍：

• 快速排序可以说是目前所有排序算法中，最快的一种排序算法。当然，没有任何一种算法是在任意情况下都是最优的。但是，大多数情况下快速排序是比较好的选择。

• 快速排序其实是冒泡排序的升级版；

快速排序的核心思想是分而治之，先选出一个数据（比如65），将比其小的数据都放在它的左边，将比它大的数据都放在它的右边。这个数据称为枢纽

和冒泡排序的不同：

• 我们选择的65可以一次性将它放在最正确的位置，之后就不需要做任何移动；
• 而冒泡排序即使已经找到最大值，也需要继续移动最大值，直到将它移动到最右边；

快速排序的枢纽：

• 第一种方案：直接选择第一个元素作为枢纽。但是，当第一个元素就是最小值的情况下，效率不高；
• 第二种方案：使用随机数。随机数本身十分消耗性能，不推荐；
• 优秀的解决方法：取index为头、中、位的三个数据排序后的中位数；如下图所示，按下标值取出的三个数据为：92，31，0，经排序后变为：0，31，92，取其中的中位数31作为枢纽（当（length-1）/2不整除时可向下或向上取整）：

数组经过获取枢纽函数操作之后，选出的3个下标值对应的数据位置变为：

动态过程：

快速排序代码实现：

 

// 快速排序
  // 1. 选择枢纽
  ArrayList.prototype.median = function(left, right) {
    // 取中间的位置
    let center = Math.floor((left + right) / 2);
    // 判断,进行交换
    if(this.array[left] > this.array[center]) {
      this.swap(left, center);
    }
    if(this.array[center] > this.array[right]) {
      this.swap(center, right);
    }
    if(this.array[left] > this.array[right]) {
      this.swap(left, right);
    }

    // 返回枢纽数值
    return this.array[center];
  }
  // 2. 快速排序的实现
  ArrayList.prototype.quickSort = function() {
    if (this.array.length == 0) {
      return [];
    }
    this.quick(0, this.array.length - 1);
  }
  ArrayList.prototype.quick = function(left, right) {
    // 1. 结束条件
    if(left >= right) return;
    // 2. 读取枢纽
    let pivot = this.median(left, right);
    console.log(pivot);
    // 3. 定义变量.用于记录当前找到的位置
    // i 小于枢纽位置
    // j 大于枢纽位置
    let i = left + 1;
    let j = right -1;
    // 4. 开始进行交换
    while(true) {
      // 如果左边的迭代器小于枢纽位置的值则一直向右寻找
      while(this.array[i] < pivot) {i++}
        // 如果右边的迭代器大于枢纽位置的值则一直向左寻找
      while(this.array[j] > pivot) {j--}
        // 如果左边的迭代器和右边的迭代重合了或者大于了则退出循环
      if(i >= j) {
        break;
      }
      // 6. 如果两个都找到了对应的值，则让他们进行交换位置,
      this.swap(i, j);
      // 7.分而治之
      this.quick(left, i - 1);
      this.quick(i + 1, right);
    }
  }

 快速排序  比较容易理解，但是内存占用较多的实现方法

 

 

//交换两个位置的数据
let swap = function(arr, m, n){
    let temp  = arr[m]
    arr[m] = arr[n]
    arr[n] = temp
}

//快速排序
//1.选择枢纽
let median = function(arr){
  //1.取出中间的位置
  let center = Math.floor(arr.length / 2)
  let right = arr.length - 1 
  let left = 0

  //2.判断大小并进行交换
  if (arr[left] > arr[center]) {
    swap(arr, left, center)
  }
  if (arr[center] > arr[right]){
    swap(arr, center, right)
  }
  if (arr[left] > arr[right]) {
    swap(arr, left, right)
  }
  //3.返回枢纽
  return center
}
//2.快速排序
let QuickSort = function(arr){
  if (arr.length == 0) {
    return []
  }
  let center = median(arr)
  let c = arr.splice(center, 1)
  let l = []
  let r = []

  for (let i = 0; i < arr.length; i++) {
      if (arr[i] < c) {
        l.push(arr[i])
      }else{
        r.push(arr[i])
      }        
  }
  return QuickSort(l).concat(c, QuickSort(r))
}

 

快速排序的效率：

• 快速排序最坏情况下的效率：每次选择的枢纽都是最左边或最右边的数据，此时效率等同于冒泡排序，时间复杂度为O（n^2^）。可根据不同的枢纽选择避免这一情况；
• 快速排序的平均效率：为O（N*logN），虽然其他算法效率也可达到O（N*logN），但是其中快速排序是最好的。