离散数学P6 Graph Theory and Coloring

【P6】 -Mathematics for Computer Science_哔哩哔哩_bilibili

Claim(University Chicago): on average, men have 74% more opposite gender partners than women.

Claim(ABC News):on average, men have 233% more opposite gender partners than women.

 

Def:A graph G is a pair  of sets (V, E) where 

V is a nonempty set of items called vertices or nodes.

and E is a set of 2-items subsets of V called edges.

🔍 区别和倾向用法

术语	领域倾向	含义与用法解释
Vertex / Vertices	更偏向数学图论术语（Graph Theory）	强调的是图的结构和拓扑关系，源自几何
Node / Nodes	更偏向计算机科学或网络分析	强调点作为实体、单元，如数据结构、网络中的计算单元、树的节点

Sample:

V:{x1,x2,x3,x4,x5,x6,x7}

E:{{x1,x2}, {x1,x3}, ..., {x5,x7}}  边的表示也可以x1-x2，有向图的时候加个箭头x1->x2

V不可以为空，E可以为空∅

 

Def: Two nodes xi and xj are adjacent, if {xi,xj}∈E

Def: An edge e={xi,xj} is incident to xi and xj.

在图论中：

A vertex $v$ and an edge e are incident if v is one of the endpoints of $e$。

也就是说，如果一个点在某条边的两端之一，就说这条边“incident to”这个点。

 

Def: the number of edges incident to a node is the degree of the node.

Def: A graph is simple if it has no loops or multiple edges.  loop是一个node自己连接自己， multiple edges是两条边连接的node是相同的。

 

Def:Am = average # of opposite gender partners for men.

Def:Aw = average # of opposite gender partners for women.

What is Am/Aw=? 1.74, 3.33

Am=Sumx属于Vm的deg(x)/Vm=|E|/|Vm|

Aw=Sumx属于Vw的deg(x)/Vw=|E|/|Vw|

Bipartite graph（二部图） 是图论中一种结构清晰、性质良好的图。以下是它的定义、关键特性、判定条件、应用与推论的系统整理。

一个无向图 G = (V, E) 是二部图（bipartite graph），当且仅当其顶点集 V 可以分成两个不相交的子集 V1​ 和 V2​，满足：

每一条边都连接一个来自 V1​ 的点和一个来自 V2 的点，即不存在任何一条边连接同一子集内的两个顶点。

 

Am/Aw=(E/Vm)/(E/Vw)=(E/Vm)*(Vw/E)=Vw/Vm=1.0325

 

给不同的课程排期末考试的时间，引入graph coloring问题

Graph coloring problem：Given a graph G and K colors, assign a color to each node, so that adjacent nodes get different colors.

Def: The minimum value of K for which such a coloring exists is the Chromatic Number of G. 着色数χ(G)

 

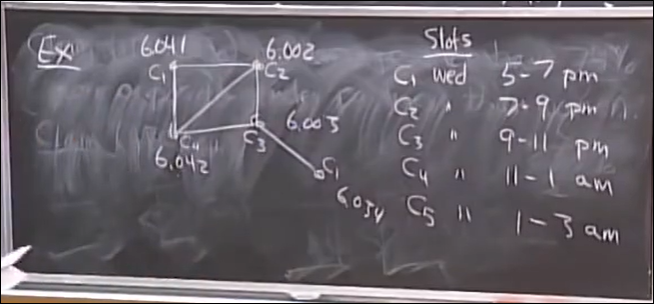
Bacic Coloring Algorithm: for G(V,E)

1.Order the nodes V1,V2,...,Vn

2.Order the colors C1,C2,...

3.For i=1,2,...,n

   Assign the lowest legal color Vi

 

Theorem: If every node in n-node G has degree<=d, the Basic Algorithm uses at most d+1 colors for G.

Proof by induction:

Suppose a graph with n nodes

Base Case: n=1, 0 edges, and degree is 0, and 1 color works, so d+1 is true

Inductive Step:Assume P(n) is true for induction

Let G=(V,E) be any (n+1)-node graph. Let d=max degree in G

Order the nodes V1,V2,...,Vn.Vn+1

Remove Vn+1 from G to create G'=(V', E')  移除一个node，不会让degree变大

G' has max degree<=d and n nodes, so P(n) says Basic Algorithm uses d+1 corlors for V1,V2,...,Vn

Vn+1 has <=d neighbors  因为P(n+1)的degree1，假设就是Vn+1这个node

there exist color in {C1,C2,...,Cd+1} not used by any neighbors

Give Vn+a that color.

=>Basic Algorithm uses <=d+1 colors for G=>P(n+1)

 

 

Def: A graph G(V,E) is bipartite if V can be split into VL and VR, so that all eges connect a node in VL to a node in VR.