激活函数

在最初的感知模型中，输入和输出的关系：

                                                                                                               

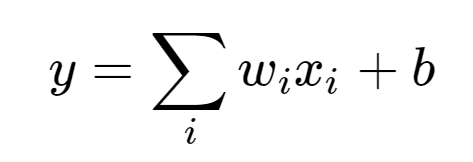
只有单纯的线性关系，当很多这样结构的网络层叠加，输入和输出还是线性的，无法处理非线性的输入和输出。因此我们可以将这个输入结果加到一个非线性函数中（激活函数）中，来进行非线性转化。

Sigmoid激活函数

                                                                                   

当网络层数较少的时候，可以很好的满足激活函数的作用。可以将实数压缩到0到1之间。当数字较大时，结果接近1；当输入是一个非常大的负数时，结果接近0。这种特性，能够很好的模拟神经元受刺激后，是否被激活反向传递信息（输出为0时，几乎不激活；输出为1时，完全被激活）

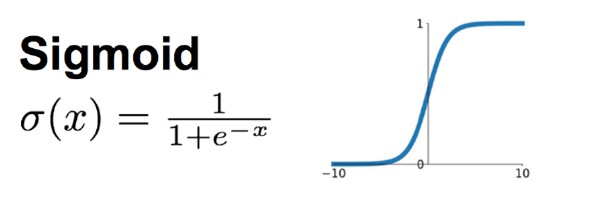
缺点：一个很大的问题就是梯度饱和，当输入的数字较大或较小的时候，其函数值趋于不变，导数变的非常小。在层数很多的神经网络中，进行反向传播时，由于很多很小的Sigmoid导数累成，导致其结果趋于0，权重更新慢。

Relu激活函数

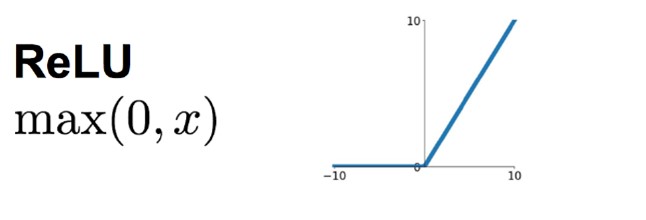
ReLU是一个分段线性函数，小于等于0则输出为0；大于0则恒等输出。

sigmoid的正向传播有指数运算，倒数运算，而Relu是线性输出；反向传播中，sigmoid有指数运算，而Relu有输出的部分，导数始终为1

Relu会使一部分的神经元输出为0，这样可以造成网络的稀疏性，并且减少参数的相互依存关系，缓解了过拟合的发生。

原理：本身虽然是一个线性的分段函数，但是可以把神经网络看成一个巨大的变换矩阵M，输入为所有训练样本组成的矩阵A，输出为矩阵B。

B = M *A

对于Relu来说，由于其是分段的，0的部分可以看成神经元没有激活，不同的神经元激活或者不激活，其神经元所组成的变换矩阵是不一样的。

每个训练样本使用的线性变换矩阵Mi是不一样的，对于整个训练样本空间来说，其经历的是非线性变换