N皇后问题
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
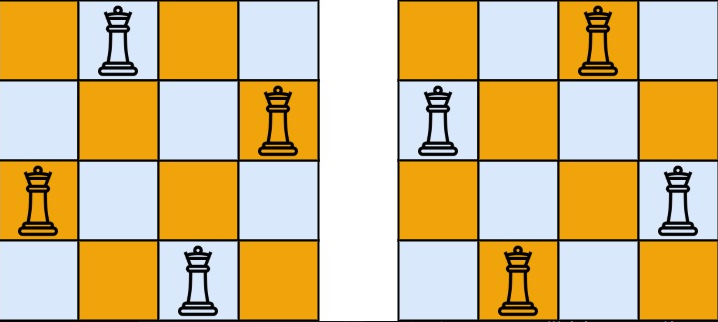
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[["Q"]]
想法:首先这里要用模板来解决这个问题:
//void backtracking(参数) { // if (终止条件) { // 存放结果; // return; // } // for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) { // 处理节点; // backtracking(路径,选择列表); // 递归 // 回溯,撤销处理结果 // } //}
- 首先是参数的问题,这里的参数应该包含,棋盘的大小n,新创建的棋盘,还有每次的行数,也就是n.chessboard,row
- 其次是最后的终止条件,这里只要row==n那么就返回。
- 节点上面的处理,要是这个点放进去判断的时候发现没有同行,同列,两个斜角都没有皇后,那就是合理的。
-
class Solution { public: vector<vector<string>>res; bool isval(int row,int i,vector<string>& chessboard,int n) { //检查列上是不是有皇后 for (int j = 0; j < row; j++) { if (chessboard[j][i] == 'Q') { return false; } } //检查45°角上 for (int j = row - 1, k = i - 1; j >= 0 && k >= 0; j--, k--) { if (chessboard[j][k] == 'Q') { return false; } } //检查135°角上 for (int j = row - 1, k = i + 1; j >= 0 && k < n; j--, k++) { if (chessboard[j][k] == 'Q') { return false; } } return true; } void backtracking(int n,int row,vector<string>& chessboard) { if (row == n) { res.push_back(chessboard); return; } for (int i = 0; i < n; i++) { if (isval(row,i,chessboard,n)) { chessboard[row][i] ='Q'; backtracking(n,row+1,chessboard); chessboard[row][i] = '.'; } } } vector<vector<string>> solveNQueens(int n) { vector<string>chessboard(n,string(n,'.')); backtracking(n,0,chessboard); return res; } };



 浙公网安备 33010602011771号
浙公网安备 33010602011771号