学习笔记：决策单调性优化DP

决策单调性优化是对求最优化DP问题加速转移的一种方法。

前缀转移

形如 \(f(i) = \min\limits_{j<i} g(j)+w(j,i)\) 的转移方程被称为前缀转移方程，本质上就是划分区间。

若 \(f=g\)，称它为自转移；否则称为他转移。

我们称转移到 \(i\) 的 \(j\) 为决策点，记为 \(opt(i)\)，\(i\) 为被决策点。对于同一个 \(i\) 可能存在多个决策点。

对于前缀转移，决策单调性的定义如下：

• 若 \(i_1\le i_2\)，

• 对于任意 \(opt(i_1)\)，存在 \(opt(i_2)\ge opt(i_1)\)，

• 对于任意 \(opt(i_2)\)，存在 \(opt(i_1)\le opt(i_2)\)。

显然所有 \(i\) 的最左侧的 \(opt(i)\) 是单调的。

分治

若 \(f\) 是前缀转移，且是他转移，则可以用分治求解。

• 初始 \([l,r]=[1,n]\)，

• 记 \(mid = \frac{l+r}{2}\)，求解 \(opt(mid)\)，

• 递归到 \([l, mid - 1]\)，并只用在 \([l,opt(mid)]\) 中找决策点，

• 递归到 \([mid + 1, r]\)，并只用在 \([opt(mid),r]\) 中找决策点，

• 复杂度 \(O(n\log n)\)。

若 \(f\) 为自转移，需要进行更多讨论。

四边形不等式

若对于任意 \(a\le b\le c\le d\)，有 \(w(a,c) + w(b,d)\le w(b,c) + w(a,d)\)，则 \(w\) 满足四边形不等式。可简记为 "相交小于包含"。

定理 \(1\)

若 \(w\) 满足四边形不等式，则 \(f\) 具有决策单调性。

证明 \(1\)

考虑反证，假设 \(f\) 不满足决策调性，但满足四边形不等式。设 \(opt(c) = b\)，\(opt(d) = a\)，\(a< b\le c< d\)，这里都取最左侧决策点，

则有 \(g(a)+w(a,d)\le g(b)+w(b,d)\)，\(g(b)+w(b,c)< g(a)+w(a,c)\)，

因此 \(g(a)-g(b)+w(a,d)-w(b,d)\le 0<g(a)-g(b)+w(a,c)-w(b,c)\)，两边同时消去 \(g(a)-g(b)\)，则 \(w\) 不满足四边形不等式，与假设矛盾。

定理 \(2\)

我们将四边形不等式变形为 \(w(a,d)-w(a,c)\ge w(b,d)-w(b,c)\)，则 \((g(a)+w(a,d))-(g(a)+w(a,c)) \ge (g(b)+w(b,d))-(g(b)+w(b,c))\)，

形象地说，被决策点增大时，越靠后的决策点，转移的代价的增量越小，

那么对于决策点 \(j_1<j_2\)，存在一个分界点 \(x>j_2\)，使得 \(j_2<i<x\) 的决策点由 \(j_1\) 转移，\(i\ge x\) 的决策点由 \(j_2\) 转移。

我们不妨把这个性质称为，"逐渐变劣"性质。

LGP3515 [POI 2011] Lightning Conductor

Solution

\(a_j\le a_i+p_i-\sqrt{|i-j|}\)，

\(p_i = \max\limits_{j} a_j-a_i+\sqrt{|i-j|} = \max\{\max\limits_{j<i}a_j-a_i+\sqrt{i-j}, \max\limits_{j>i}a_j-a_i+\sqrt{j-i}, 0\}\)，

分两遍求，接下来证明左边满足决策单调性，右边同理。

设 \(w(i,j) = a_j - a_i + \sqrt{i-j}\)，设 \(i<j<k<t\)，

\(w(i,k)+w(j,t) - w(i,t)-w(j,k) = \sqrt{k-i}-\sqrt{k-j}-(\sqrt{t-i}-\sqrt{t-j})\)，

由于 \(y=\sqrt x\) 这个函数随着 \(x\) 增大，每次变化量越来越小，因此上面的式子 \(>0\)，由于是 \(\max\)，因此四边形不等式要变成 \(\ge\)，因此 \(w\) 满足四边形不等式，也就满足决策单调性。

Code

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using ULL = unsigned long long;
using LD = long double;
using PII = pair<int, int>;

const int N = 5e5 + 5;
double INF = 2e9 + 5;

int n;
double a[N], f0[N], f1[N];

void work0(int l, int r, int L, int R) {
    if (l > r) return;
    int mid = l + r >> 1, cur = 0;
    for (int i = L; i <= min(R, mid - 1); i++) {
        double val = a[i] - a[mid] + sqrt(mid - i);
        if (val > f0[mid]) {
            cur = i;
            f0[mid] = val;
        }
    }
    work0(l, mid - 1, L, cur);
    work0(mid + 1, r, cur, R);
}

void work1(int l, int r, int L, int R) {
    if (l > r) return;
    int mid = l + r >> 1, cur = 0;
    for (int i = R; i >= max(L, mid + 1); i--) {
        double val = a[i] - a[mid] + sqrt(i - mid);
        if (val > f1[mid]) {
            cur = i;
            f1[mid] = val;
        }
    }
    work1(l, mid - 1, L, cur);
    work1(mid + 1, r, cur, R);
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) f0[i] = f1[i] = -INF;
    work0(1, n, 1, n);
    work1(1, n, 1, n);
    for (int i = 1; i <= n; i++) cout << (int)ceil(max({f0[i], f1[i], 0.0})) << '\n';
    return 0;
}

CF321E Ciel and Gondolas

Solution

设 \(f(i,j)\) 表示前 \(i\) 个人划分成 \(k\) 段的最小价值，

\(f(i,j) = \min\limits_{k<i} f(k,j-1)+w(k+1,j)\)，\(w(i,j)=\sum\limits_{k=i}^{j} \sum\limits_{t=k}^{j} u(k,t)\)，

显然 \(w\) 满足四边形不等式，所以做 \(k\) 次分治即可，复杂度 \(O(kn\log n)\)。

Code

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using ULL = unsigned long long;
using LD = long double;
using PII = pair<int, int>;

namespace FastIO {
    template <typename T>
    inline T read() {
        T x = 0, w = 1;
        char ch = 0;
        while (ch < '0' || ch > '9') { if (ch == '-') w = -1; ch = getchar(); }
        while (ch >= '0' && ch <= '9') { x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar(); }
        return x * w;
    }
    template <typename T>
    inline void write(T x, char c) {
        static T sta[35];
        T top{};
        do { sta[top++] = x % 10, x /= 10; } while(x);
        while (top) putchar(sta[--top] + 48);
        putchar(c);
    }
} using FastIO::read, FastIO::write;

const int N = 4005, INF = 1e9;

int n, k, a[N][N], dp[2][N];

inline int get_sum(int x1, int y1, int x2, int y2) {
    return a[x2][y2] - a[x2][y1 - 1] - a[x1 - 1][y2] + a[x1 - 1][y1 - 1];
}

void work(int l, int r, int L, int R, int now) {
    if (l > r) return;
    int mid = l + r >> 1, val = 0, cur = 0;
    dp[now][mid] = INF;
    for (int i = min(R, mid); i >= L; i--) {
        val = get_sum(i, i, mid, mid) / 2 + dp[now ^ 1][i - 1];
        if (val < dp[now][mid]) {
            dp[now][mid] = val;
            cur = i;
        }
    }
    work(l, mid - 1, L, cur, now);
    work(mid + 1, r, cur, R, now);
}

int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            a[i][j] = read<int>();
            a[i][j] += a[i][j - 1] + a[i - 1][j] - a[i - 1][j - 1];
        }
        dp[0][i] = INF;
    }
    // for (int i = 1; i <= n; i++) {
    //     for (int j = 1; j <= n; j++) {
    //         cout << a[i][j] << ' ';
    //     }
    //     cout << '\n';
    // }
    for (int i = 1; i <= k; i++) work(1, n, 1, n, i & 1);
    write<int>(dp[k & 1][n], '\n');

    return 0;
}

定理 \(3\)

若对于任意 \(a< b\)，有 \(w(a,b)+w(a-1,b-1)\le w(a-1,b)+w(a,b-1)\)，

那么 \(w\) 满足四边形不等式。

证明 \(3\)

必要性显然满足，下证充分性。

对于 \(b\le d\)，有
\(w(b,d)+w(b-1,d-1)\le w(b-1,d)+w(b,d-1)\)，\((1)\)
\(w(b-1,d)+w(b-2,d-1)\le w(b-2,d)+w(b-1,d-1)\)，\((2)\)

\((1)+(2)\) 得，\(w(b,d)+w(b-2,d-1)\le w(b-2,d)+w(b,d-1)\)，

不妨设 \(a=b-k\)，\(a\le b\)，那么通过这样不断减一，可以得到，
\(w(b,d)+w(a,d-1)\le w(a,d)+w(b,d-1)\)，\((3)\)

假设 \(d-1\ge b\)，那么有，
\(w(b,d-1)+w(a,d-2)\le w(a,d-1)+w(b,d-2)\)，\((4)\)

\((3)+(4)\) 得，\(w(b,d)+w(a,d-2)\le w(a,d)+w(b,d-2)\)，

不妨设 \(c=d-k\)，\(b\le c\le d\)，那么通过不断减一，可以得到，
\(w(b,d)+w(a,c)\le w(a,d)+w(b,c)\)，

证毕。

LGP4767 [IOI 2000] 邮局 加强版

Solution

首先可以发现，每个邮局控制的村庄一定是一段区间，那么原问题等价于把 \(n\) 个村庄划分成 \(m\) 个区间的最小代价。

设 \(dp(i,j)\) 表示将前 \(i\) 个村庄划分为 \(j\) 个区间的最小代价。\(dp(i,j)=\min\limits_{1\le k\le i} dp(k-1,j-1)+w(k,i)\)。

设 \(w(l,r)\) 表示区间 \([l,r]\) 的代价，容易发现把邮局放在 \(\lfloor \frac{l+r}{2}\rfloor\) 的位置是最优的，于是可以写出递推式 \(w(l,r)=w(l,r-1)+X(r)-X(\lfloor \frac{l+r}{2}\rfloor)\)。

这个式子为什么是对的？若 \([l,r-1]\) 长度为奇数，\(\lfloor \frac{l+r-1}{2}\rfloor = \lfloor \frac{l+r}{2}\rfloor\)；若为偶数，\(\lfloor \frac{l+r-1}{2}\rfloor+1=\lfloor \frac{l+r}{2}\rfloor\)，中点会移动一格，但是左边增加的距离和右边减少的距离抵消了，因此也是对的。

移项得到 \(w(l,r)-w(l,r-1)=X(r)-X(\lfloor \frac{l+r}{2}\rfloor)\)，\((1)\)

\(w(l-1,r)-w(l-1,r-1)=X(r)-X(\lfloor \frac{l+r-1}{2}\rfloor)\)，\((2)\)

由 \((1) - (2)\) 得，原式 \(= X(\lfloor \frac{l+r-1}{2}\rfloor)-X(\lfloor \frac{l+r}{2}\rfloor)\le 0\)，

于是 \(w(l,r)-w(l,r-1)-w(l-1,r)+w(l-1,r-1)\le 0\)，

\(w(l,r)+w(l-1,r-1)\le w(l,r-1)+w(l-1,r)\)，

因此 \(w\) 是满足四边形不等式的。

于是分治 \(O(mn\log n)\) 求解即可。

Code

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using ULL = unsigned long long;
using LD = long double;
using PII = pair<int, int>;

const int N = 3005, INF = 2e9;

int n, m, a[N], w[N][N], dp[2][N];

void work(int l, int r, int L, int R, int now) {
    if (l > r) return;
    int mid = l + r >> 1, cur = 0;
    dp[now][mid] = INF;
    for (int i = L; i <= min(R, mid); i++) {
        int val = dp[now ^ 1][i - 1] + w[i][mid];
        if (val < dp[now][mid]) {
            dp[now][mid] = val;
            cur = i;
        }
    }
    work(l, mid - 1, L, cur, now);
    work(mid + 1, r, cur, R, now);
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        dp[0][i] = INF;
    }
    sort(a + 1, a + 1 + n);
    for (int len = 2; len <= n; len++) {
        for (int l = 1; l + len - 1 <= n; l++) {
            int r = l + len - 1;
            w[l][r] = w[l][r - 1] + a[r] - a[l + r >> 1];
        }
    }
    for (int i = 1; i <= m; i++) work(1, n, 1, n, i & 1);
    cout << dp[m & 1][n] << '\n';
    return 0;
}

定理 \(4\)

对于限制区间个数的问题，设 \(f(i,j)\) 表示将 \([1,i]\) 划分为 \(j\) 个区间的最小代价，\(f(i,j)=\min\limits_{1\le k\le i} f(k-1,j-1)+w(k,i)\)。

若 \(w\) 满足决策单调性，则 \(opt(i,j-1)\le opt(i,j)\le opt(i+1,j)\)。

根据这个定理，我们倒序枚举第一维，正序枚举第二维，即可保证 \(f(i,j-1)\) 和 \(f(i+1,j)\) 在 \(f(i,j)\) 前被求解，它们的 \(opt\) 就可以记录下来，于是可以在 \([opt(i,j-1),opt(i+1,j)]\) 这个区间内查找 \(opt(i,j)\)，

但是要注意这里的复杂度并不是 \(O(nm)\)。考虑我们要求解一个 \(n\times m\) 的状态矩阵，那么对于 \(i-j\) 为定值的 \(f(i,j)\)，在矩阵中为一条对角线，总共的枚举次数为 \(O(n)\)，但是这样的对角线有 \(O(n+m)\) 条，所以复杂度为 \(O(n(n+m))\)。

证明 \(4\)

\(opt(i,j)\le opt(i+1,j)\) 就是第一维的决策单调性，前面已经证过了。

考虑反证，设 \(opt(i,j-1) > opt(i,j)\)，

对于问题 \(f(i,j)\)，假设其在 \([1,i]\) 的最优划分为，\([a_j,b_j]\dots [a_1,b_1]\)，
对于问题 \(f(i,j-1)\)，假设其在 \([1,i]\) 最优划分为，\([c_{j-1},d_{j-1}]\dots [c_1,d_1]\)，注意这里标号是倒序的。

若 \(opt(i,j-1) > opt(i,j)\)，则有 \(a_1 < c_1\)。

若 \(a_k<c_k\)，显然 \(b_{k-1}<d_{k-1}\)。

因为我们一直是从左往右考虑，\(opt(b_j)=a_j\)，\(opt(d_j)=c_j\)；假若我们以 \(i\) 为起点，从右往左考虑，那么有 \(opt'(a_j)=b_j\)，\(opt'(c_j)=d_j\)，这时候，\(f'(x,y)\) 就表示把 \([x,i]\) 划分为 \(y\) 个区间的最小代价，那么对于 \(opt(a_{k-1})=b_{k-1}\) 和 \(opt(c_{k-1})=d_{k-1}\)，可以看成是同一个维度的问题 \(f'(*,k-1)\) 的决策点，由于同一维度的决策单调性我们已经证过了，所以 \(a_{k-1}<c_{k-1}\)，

那这样不断迭代下去，得到 \(a_{j-1} < c_{j-1}\)，这显然不能成立，于是 \(opt(i,j)\le opt(i+1,j)\) 得证。

LGP4767 [IOI 2000] 邮局 决策单调性二次优化

Code

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using ULL = unsigned long long;
using LD = long double;
using PII = pair<int, int>;

const int N = 3005, INF = 2e9;

int n, m, a[N], w[N][N], dp[N][305], opt[N][305];

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        opt[i][0] = 1; // 处理边界
        dp[i][0] = INF;
    }
    sort(a + 1, a + 1 + n);
    for (int len = 2; len <= n; len++) {
        for (int l = 1; l + len - 1 <= n; l++) {
            int r = l + len - 1;
            w[l][r] = w[l][r - 1] + a[r] - a[l + r >> 1];
        }
    }
    for (int j = 1; j <= m; j++) {
        opt[n + 1][j] = n; // 处理边界
        for (int i = n; i >= 1; i--) {
            dp[i][j] = INF;
            for (int k = opt[i][j - 1]; k <= min(i, opt[i + 1][j]); k++) {
                if (dp[k - 1][j - 1] + w[k][i] < dp[i][j]) {
                    dp[i][j] = dp[k - 1][j - 1] + w[k][i];
                    opt[i][j] = k;
                }
            }
        }
    }
    cout << dp[n][m] << '\n';
    return 0;
}

二分队列

能用二分队列的前提是满足 "逐渐变劣"性质，也就是四边形不等式，而不仅仅是普通决策单调性的定义。

设 \(x_j\) 表示决策点 \(j\) 在分界点 \(x_j\) 之后劣于决策点 \(j+1\)，

因此，若 \(x_{j-1}\ge x_j\)，那么在 \(j\) 变得比 \(j-1\) 更优之前，\(j+1\) 会先比 \(j\) 更优，所以 \(j\) 不可能被选择，可以不用考虑。

若重复上述删除过程，我们可以得到一系列 \(x\) 单调递增的决策点 \(j_1,j_2,\dots,j_k\)，

那么若当前被决策的是 \(i\)，然后某个 \(j\) 的 \(x_j < i\)，那么这个 \(j\) 也可以删去。

那么根据这个，我们可以考虑维护 \(x\) 递增且首项最优的决策点序列，来进行加速转移，

• 假设已经决策完 \(i-1\)，并维护了对于 \(i-1\) 的决策点序列 \(j_1,j_2,\dots,j_k\)，现在要决策 \(i\)，

• 先计算 \(i-1\) 与 \(j_k\) 的分界点 \(x_k\)，若 \(x_k \le x_{k-1}\)，则删去 \(j_k\)，不断重复，最后加入 \(i-1\)，

• 若对于 \(i\)，\(x_{j_1}<i\)，则删去 \(j_1\)，不断重复，最后的 \(j_1\) 即为 \(i\) 的决策点。

• 可以用双端队列维护决策点，并用二分求解 \(x\)。于是这种方法可以将 自转移或他转移 优化到 \(O(n\log n)\)，被称作 二分队列。

LGP1912 [NOI2009] 诗人小G

转换一下题意，给定长度为 \(n\) 的序列 \(a\)，将 \(a\) 划分成任意段，每段的代价为 \(|\sum\limits_{i=l}^{r} a_i - L|^P\)，求一种划分方案使得代价和最小。

Solution

设 \(f(i)\) 表示前 \(i\) 个划分的最小代价，有转移 \(f(i) = \min\limits_{j<i} f(j)+|S_i-S_j-L|^P\)。其中 \(S\) 为 \(a\) 的前缀和。

关于这题的决策单调性证明，我觉得用图像分析来理解的话，特别方便。

那么要证决策单调性，我们考虑能不能从 四边形不等式 或者 "逐渐变劣"性质 来证明。

设 \(w_i(j) = |S_j-S_{i}-L|^P\)，是一个关于 \(j\) 的函数，

那么我们可以把 \(f\) 的转移方程改写为，\(f(i) = \min\limits_{j<i} f(j)+w_j(i)\)，

接下来要证明 \(w_a(d)-w_a(c)\ge w_b(d)-w_b(c)\)，\(a<b<c<d\)，也就是 "逐渐变劣"性质。

由于 \(w_b(x) = w_a(x+C)\)，其中 \(C=S_a-S_b\)，我们都知道，函数自变量加上一个常数，就相当于左右平移。

可以先画出 \(w_a\) 和 \(w_b\) 的图像，大概是这样的，

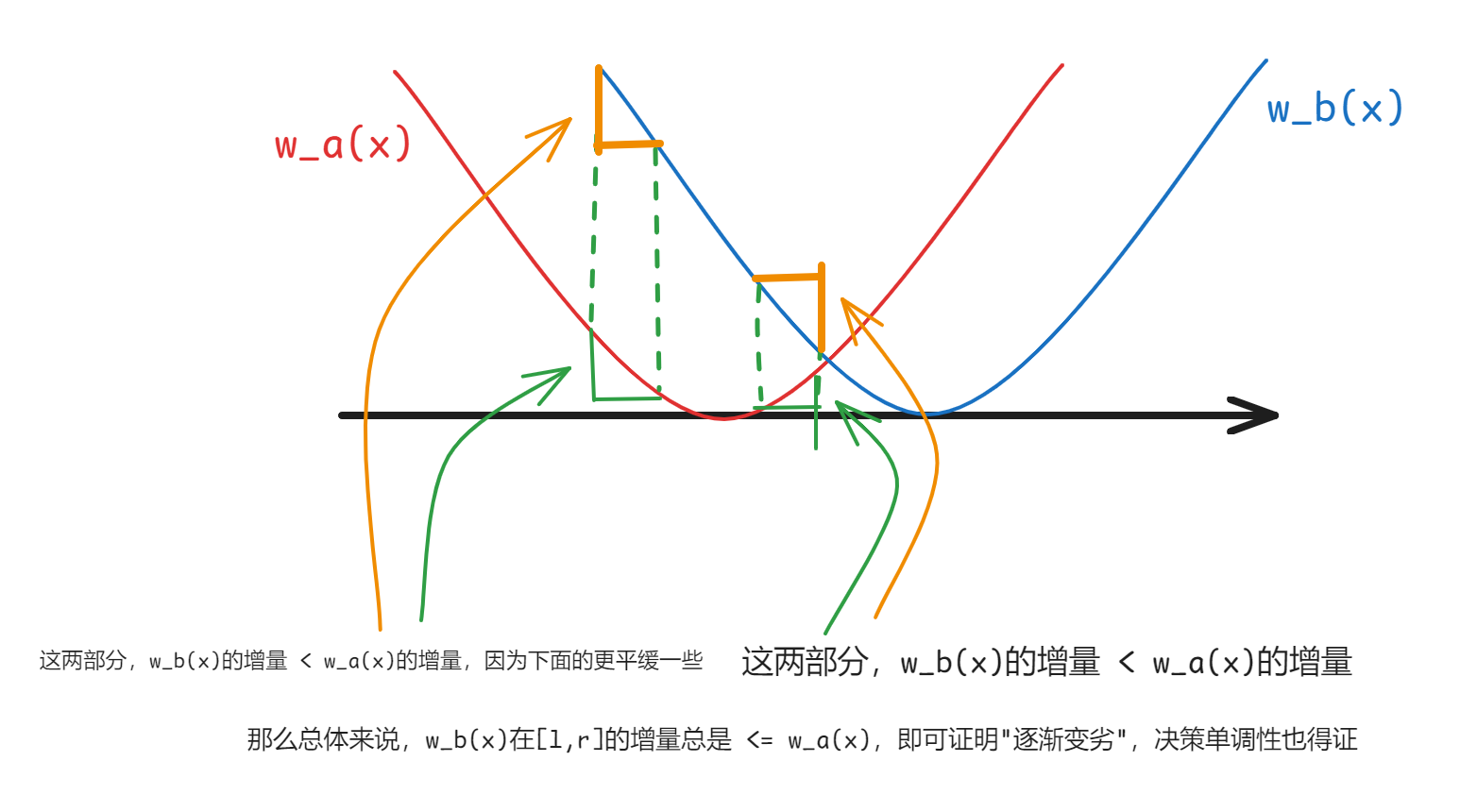
于是就证明了决策单调性，由于是自转移，用二分队列即可。

注意题目中的 \(a_i\) 还要算上空格，因此初始让 \(a_i=len(string)+1\)，然后 \(L+1\) 即可，因为末尾没有空格，要减 \(1\)。

Code

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using ULL = unsigned long long;
using LD = long double;
using PII = pair<int, int>;

const int N = 1e5 + 5;

int n;
string s[N];
int pre[N], x[N];
LD f[N], a[N], L, P;

LD fpow(LD a, int b) {
    LD ans = 1;
    for (; b; b >>= 1) {
        if (b & 1) ans = ans * a;
        a = a * a;
    }
    return ans;
}

inline LD val(int j, int i) {
    if (j == i) return 0;
    return f[j] + fpow(abs(a[i] - a[j] - L), P);
}

int calc(int j, int i) {
    int l = i, r = n, mid;
    while (l < r) {
        mid = l + r + 1 >> 1;
        if (val(j, mid) <= val(i, mid)) l = mid;
        else r = mid - 1;
    }
    return r;
}

void write(int x) {
    if (!x) return;
    write(pre[x]);
    for (int i = pre[x] + 1; i <= x; i++) cout << s[i] << (i == x ? '\n' : ' ');
}

struct Deque {
    int a[N], tl, hd;

    inline void clear() { hd = 1, tl = 0; }

    inline bool empty() { return tl < hd; }

    inline void push_back(int x) { a[++tl] = x; }

    inline void pop_back() { tl--; }

    inline void pop_front() { hd++; }

    inline int front() { return a[hd]; }

    inline int back() { return a[tl]; }

    inline int size() { return tl - hd + 1; }

    inline int begin() { return hd; }

    inline int end() { return tl; }
} dq;

void Solve() {
    cin >> n >> L >> P;
    L++;
    for (int i = 1; i <= n; i++) {
        cin >> s[i];
        a[i] = s[i].size() + 1;
        a[i] += a[i - 1];
    }
    f[0] = 0;
    dq.clear();
    dq.push_back(0);
    for (int i = 1; i <= n; i++) {
        while (dq.size() > 1 && x[dq.front()] < i) dq.pop_front();
        int j = dq.front();
        f[i] = val(j, i);
        pre[i] = j;
        while (dq.size() > 1 && x[dq.a[dq.end() - 1]] >= calc(dq.back(), i)) dq.pop_back();
        x[dq.back()] = calc(dq.back(), i);
        dq.push_back(i);
    }
    if (f[n] > 1e18) {
        cout << "Too hard to arrange\n";
        cout << "--------------------\n";
        return;
    }
    cout << (LL)f[n] << '\n';
    write(n);
    cout << "--------------------\n";
}

int main() {
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    
    int T;
    cin >> T;
    for (int i = 1; i <= T; i++) Solve();

    return 0;
}

区间转移

形如 \(f(i,j)=\min\limits_{i\le k<j} f(i,k)+f(k+1,j)+w(i,j)\) 的方程被称为区间转移方程。

一般只考虑自转移的情况，否则归纳为前缀转移方程。

同样的，我们设 \(opt(i,j)\) 表示 \(f(i,j)\) 的最佳且是最左端的决策点 \(k\)，\((i,j)\) 为被决策点。

对于区间转移，决策单调性定义如下：

• 对于 \(i_1\le i_2\)，\(j_1\le j_2\)，有 \(opt(i_1,j_1)\le opt(i_2,j_2)\)。

根据决策单调性，对于 \(i<j\)，有 \(opt(i,j-1)\le opt(i,j)\le opt(i+1,j)\)，由于 \(f(i,j-1)\) 和 \(f(i+1,j)\) 比 \(f(i,j)\) 先被求解，那么可以直接在这个范围内枚举计算 \(opt(i,j)\)。于是对于同样长度的区间，枚举次数和为 \(O(n)\)，一共有 \(O(n)\) 种长度，所以复杂度从朴素的 \(O(n^3)\) 优化到了 \(O(n^2)\)。

区间包含单调性

若对于 \(a\le b\le c\le d\)，有 \(w(b,c)\le w(a,d)\)，则称 \(w\) 满足区间包含单调性。

本质上是要求 \(w(i,j)\) 关于 \(i\) 递减，关于 \(j\) 递增。

定理 \(5\)

若 \(w\) 同时满足四边形不等式和区间包含单调性，则 \(f\) 满足决策单调性。

证明 \(5\)

先证明若 \(w\) 同时满足四边形不等式和区间包含单调性，则 \(f\) 也满足四边形不等式。

设 \(a\le b\le c\le d\)，

考虑数学归纳法，按照 \(d-a\) 从小到大的顺序归纳。

首先对于 \(d-a=0\) 的情况，显然是成立的。

设 \(e = opt(a,d)\)，

• 若 \(c\le e\) 或 \(e < d\)，不妨设 \(c\le e\)，第二种情况同理。

  • \(f(a,d)+f(b,c) = f(a,e)+f(e+1,d)+w(a,d)+f(b,c)\)，

  • 因为 \(e-a<d-a\)，根据归纳假设，有 \(f(a,d)+f(b,c)\ge f(a,c)+f(b,e)+f(e+1,d)+w(a,d)\)，

  • 根据 \(w\) 的区间包含单调性，有 \(f(a,d)+f(b,c)\ge f(a,c)+f(b,e)+f(e+1,d)+w(b,d)\)，

  • 因为 \(f(b,d)\le f(b,e)+f(e+1,d)+w(b,d)\)，所以得到 \(f(a,d)+f(b,c)\ge f(a,c)+f(b,d)\)。

• 若 \(b\le e<c\)，设 \(p=opt(b,c)\)，不妨设 \(p\le e\)，第二种 \(p>e\) 的情况同理。

  • \(f(a,d)+f(b,c)=f(a,e)+f(e+1,d)+w(a,d)+f(b,p)+f(p+1,c)+w(b,c)\)，

  • 同样根据归纳假设，\(f(a,d)+f(b,c)\ge f(a,p) + f(p+1,c)+w(b,c)+f(b,e)+f(e+1,d)+w(a,d)\)，

  • 根据 \(w\) 的四边形不等式，\(f(a,d)+f(b,c)\ge f(a,p)+f(p+1,c)+w(a,c)+f(b,e)+f(e+1,d)+w(b,d)\)，

  • 第三步和上面第三步同理，\(f(a,d)+f(b,c)\ge f(a,c)+f(b,d)\)。

因此 \(f\) 满足四边形不等式。

下证，若 \(f\) 满足四边形不等式，则 \(f\) 满足决策单调性 \(opt(i,j-1)\le opt(i,j)\le opt(i+1,j)\)，

设 \(g_i(k,j)=f(i,k)+f(k+1,j)+w(i,j)\)，代入并消去相同的项，容易算出，\(g_i(a,d)+g_i(b,c)\ge g_i(a,c)+g_i(b,d)\)，即 \(g_i\) 满足四边形不等式。

又因为 \(f(i,j)=\min g_i(k,j)\)，因此根据定理 \(1\)，容易得到 \(f(i,j)\) 关于 \(j\) 满足决策单调性，即 \(opt(i,j-1)\le opt(i,j)\)。

设 \(h_j(i,k)=f(i,k)+f(k+1,j)+w(i,j)\)，类似的，也可以得到 \(h_j\) 满足四边形不等式。

又因为 \(f(i,j)=\min h_j(i,k)\)，得到 \(f(i,j)\) 关于 \(i\) 也满足决策单调性，即 \(opt(i,j)\le opt(i+1,j)\)。

证毕。

LGP1880 [NOI1995] 石子合并

含 最大值问题只用取两个端点转移 的证明。

Solution

设 \(f(l,r)\) 表示将 \([l,r]\) 合并的最小代价。

\(f(l,r)=\min\limits_{l\le k<j} f(l,k) + f(k+1,r) + w(l,r)\)，\(w\) 是区间和，显然满足四边形不等式和区间包含单调性，直接优化即可。

若要求的是最大值，\(w\) 仍满足反四边形不等式，但是不满足反区间包含单调性，因此不能这样优化。

设 \(g(l,r)\) 表示最大值，下面我们证明 \(g(l,r) = \max\{g(l+1,r),g(l,r-1)\}+w(l,r)\)，

假设当前要解决 \(g(l,r)\)，设 \(l<q<p<r\)，

不妨设 \(w(l,p)\le w(p+1,r)\)，另一种情况同理。

若 \(g(l,r)\) 从 \(p\) 转移，\(g(l,p)\) 从 \(q\) 转移，有 \(g_1(l,r)=g(l,q)+g(q+1,p)+w(l,p)+g(p+1,r)+w(l,r)\)，

若 \(g(l,r)\) 从 \(q\) 转移，\(g(r,p)\) 从 \(q\) 转移，有 \(g_2(l,r)=g(l,q)+g(q+1,p)+g(p+1,r)+w(q+1,r)+w(l,r)\)，

因为 \(w(l,q)\le w(p+1,r)< w(q+1,r)\)，因此 \(g_1(l,r)<g_2(l,r)\)，所以转移点要尽量靠左。同理可得，另一种情况 \(w(l,q)\ge w(p+1,r)\) 时转移点要尽量靠右。

证毕。

Code

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using ULL = unsigned long long;
using LD = long double;
using PII = pair<int, int>;

const int N = 205, INF = 2e9;

int n, a[N], f[N][N], g[N][N], opt[N][N];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        a[n + i] = a[i];
    }
    for (int i = 1; i <= n * 2; i++) {
        a[i] += a[i - 1];
        opt[i][i] = i;
    }
    for (int len = 2; len <= n; len++) {
        for (int l = 1; l + len - 1 <= n * 2; l++) {
            int r = l + len - 1;
            f[l][r] = INF;
            for (int k = opt[l][r - 1]; k <= min(r - 1, opt[l + 1][r]); k++) {
                if (f[l][k] + f[k + 1][r] < f[l][r]) {
                    f[l][r] = f[l][k] + f[k + 1][r];
                    opt[l][r] = k;
                }
            }
            f[l][r] += a[r] - a[l - 1];
        }
    }
    for (int len = 2; len <= n; len++) {
        for (int l = 1; l + len - 1 <= n * 2; l++) {
            int r = l + len - 1;
            g[l][r] = max(g[l + 1][r], g[l][r - 1]) + a[r] - a[l - 1];
        }
    }
    int mn = INF, mx = -INF;
    for (int i = 1; i <= n; i++) {
        mn = min(mn, f[i][i + n - 1]);
        mx = max(mx, g[i][i + n - 1]);
    }
    cout << mn << '\n' << mx << '\n';
    return 0;
}

声明

本篇学习笔记目的是做个人笔记梳理和记录，一部分证明或理论写在这里不代表是编者原创的，而是经过整理后，加入了自己的想法，更利于自己理解的，读者仅供参考。

参考文章

• OI Wiki

• 题解 P4767 [IOI2000] 邮局

• 四边形不等式优化dp，超详细，概念定理详解证明，OJ练习