数据结构代码笔记

2020-5-9 11:08:51

2.2.2 插入,删除.查找 Demo(由于没有学C/C++,代码就那个意思,理解就好)

插入

// 插入代码
#include <iostream>

# define   InitSize 10 //默认长度

typedef struct{
    ElemType  data[MaxSize];    //用静态的数组存放数据元素
    int length;                    //顺序表的当前长度
}SqList;

//插入操作(自己写的那种) L:表  i:元素位序  e:插入元素
bool ListInsert(SqList &L, int i, int e){  
    if(i<1||i>L.length+1)    //判断i的范围是否有效
        return false;
    if(L.length>=MaxSize)    //当前存储空间已满,不能插入
        return  false;
    for(int j = L.length;j>=i; j--)    //讲第i个元素及之后的元素后移动
        L.data[j]=L.data[j-1];
    L.data[i-1]=e;                    //在位置i处放入e
    L.length++;                        //长度加1
    return true;                    
}


int main(){
    SqList  L;            //声明一个顺序表
    InitList(L);    // 初始化顺序表
    ListInsert(&L,1,0);    //插入一个元素  
    ListInsert(&L,2,1);    //插入一个元素
    ListInsert(&L,1,3);
}

按值查找

//顺序表的按值查找
#include <iostream>
typeef struct{
    int *data;        //指示动态分配数组的指针
    int MaxSize;    //顺序表的最大容量
    int length;        // 顺序表的当前长度
}SeqList

//在顺序表L中查找第一个元素值等于e的元素,并返回其位序
int LocateElem (SeqList L, int e){
    for(int i=0;i<L.length;i++)
        if(L.data[i]=e)
            return i+1;
    return 0;
}

int main(){
    SeqList(L);
    InitList(L);
    // 省略一些代码,插入一些数据
    LocateElem(L,3); // 查找元素值为3的元素
    
}

删除操作

//删除操作
#include <iostream>

# define   InitSize 10 //默认长度

typedef struct{
    ElemType  data[MaxSize];    //用静态的数组存放数据元素
    int length;                    //顺序表的当前长度
}SqList;

//删除操作(自己写的那种) L:表  i:元素位序  e:插入到的位置
bool ListDelete(SqList &L, int i , int &e){
    if|(i<1||i>L.length)    //    判断i的范围是否有效
        return false;        
    e=L.data[i-1];            // 将被删除的元素赋值给e
    for(int j=i; j<L.length;j++)    //将第i个位置后的元素前移
        L.data[j-i]=L.data[j]; //主义位序,数组下标的关系,并从前面的元素依次移动
    L.length--;    //线性表长度减1
    return true;
}

int main(){
    SqList  L;            //声明一个顺序表
    InitList(L);    // 初始化顺序表
    // ......此处省略一些代码,插入几个元素
    int e = -1;
    if(Listdelete(L,3,e))
        printf("已删除第3个元素,删除元素只为=%d\n",e);
    else
        printf("位序i不合法,删除失败\n");
}

 查找

// 查找方法
#include <iostream>
//定义一个表
typedef struct{
    ElemType  data[MaxSize];    //用静态的数组存放数据元素
    int length;                    //顺序表的当前长度
}SqList;

// 查找第几个元素
ElemType GetElem(SqList L, int i){
    return L.data[i-1]  //直接通过下标找元素
}
int main(){
    SqList  L;            //声明一个顺序表
    InitList(L);    // 初始化顺序表
    // ..省略一些代码,插入一些数据
    GetElem(&L,1);    //插入一个元素  

}

 2.3.1单链表的一些demo

1.不带头结点的单链表

#不带头结点的单链表
#include <iostream>
typedef struct LNode{    // 定义单链表节点类型
    ElemType data;        // 每个节点存放一个数据元素
    struct LNode *next;    // 指针指向下一个节点
}LNode, *LinkList;        // 通过typedef函数,定义的链表和结点别名

// 初始化一个空的单链表
bool InitList(LinkList&L){
    L = NULL;    //空表,暂时还没有任何结点 (防止脏数据)
    return true;
}

//判断单链表是否为空
bool Empty(LinkList L){
    if (L == null)
        return true;
    else
        return false;
}
//或者更简单
bool Empty(LinkList L){
    return (L== NULL);
}


int main(){
    LinkList L;        //声明一个指向单链表的指针
    InitList(L);    //初始化一个空表
    // ....后续代码
    
}

2.带头结点的单链表 (推荐使用,写代码更加方便)

//带头结点的单链表
#include <iostream>
typedef struct LNode{    // 定义单链表节点类型
    ElemType data;        // 每个节点存放一个数据元素
    struct LNode *next;    // 指针指向下一个节点
}LNode, *LinkList;        // 通过typedef函数,定义的链表和结点别名

// 初始化一个空的单链表(带头结点)
bool InitList(LinkList&L){
    L = (LNode *) malloc(sizeof(LNode));    //分配一个头结点
    if (L==NULL)        //内存不足,分配失败
        return false ;
    L->next = NULL;        // 头结点之后暂时还没有节点
    return true;
}

//判断单链表是否为空
bool Empty(LinkList L){
    if (L->next == null)
        return true;
    else
        return false;
}


int main(){
    LinkList L;        //声明一个指向单链表的指针
    InitList(L);    //初始化一个空表
    // ....后续代码
    
}

3.按位序插入(带头结点)

//按位序插入(带头结点)
#include <iostream>
typedef struct LNode{    // 定义单链表节点类型
    ElemType data;        // 每个节点存放一个数据元素
    struct LNode *next;    // 指针指向下一个节点
}LNode, *LinkList;        // 通过typedef函数,定义的链表和结点别名

// 在第i个位置插插入元素e(带头结点)
bool ListInsert(LinkList &L, int i ,ElemType e){
    // 找出 p点指针,也就是要插入的位置在位序为第i-1结点
    if(i<1);
        return false;
    LNode *p;    //指针p指向当前扫描到的结点
    int j = 0;    //当前p指向的第几个结点
    p = L         //L指向头结点,头结点是第0个结点(不存数据)
    while (p!=NULL && j<i-1){ // 循环找到第 i-1 个结点
        p=p->next;
        j++;
    }
    if(p==NULL)    //i值不合法
        return false;
    
    // 要在第i-1的结点之后插入一个新的结点
    LNode *s = (LNode *)malloc(sizeof(LNode));
    s->data = e;
    s->next=p->next;//用s指向后面指针替换了p点指向后面的指针
    p->next=s        //将结点s链接到p之后
    return true;    //插入成功
}



int main(){
    LinkList L;        //声明一个指向单链表的指针
    InitList(L);    //初始化一个空表
    // ....后续代码
    
}

4.按位  序插入(不带头结点)

#include <iostream>
typedef struct LNode{    // 定义单链表节点类型
    ElemType data;        // 每个节点存放一个数据元素
    struct LNode *next;    // 指针指向下一个节点
}LNode, *LinkList;        // 通过typedef函数,定义的链表和结点别名

// 在第i个位置插插入元素e(带头结点)
bool ListInsert(LinkList &L, int i ,ElemType e){
    // 找出 p点指针,也就是要插入的位置在位序为第i-1结点
    if(i<1);
        return false;
    if(i==1){    //插入第1个结点的操作与其他结点操作不同
        LNode *s = (LNode *)malloc(sizeof(LNode));
        s->data = e;
        s->next = L;
        L = s;    //头指针指向新结点
        return true;
    }
    LNode *p;    //指针p指向当前扫描到的结点
    int j=1;    //当前p指向的第几个结点
    p = L;        //p指向第1个结点(注意:不是头结点)
    while (p!=NULL && j<i-1){ //循环找到第 i-1个结点
        p=p->next;
        j++;
    }
    if(p==NULL)    //i的值不合法
        return  false;
    
    // 要在第i-1的结点之后插入一个新的结点
    // 插入逻辑和带头结点的一样,只是加了上面i=1的判断
    LNode *s = (LNode *)malloc(sizeof(LNode));
    s->data = e;
    s->next=p->next;//用s指向后面指针替换了p点指向后面的指针
    p->next=s        //将结点s链接到p之后
    return true;    //插入成功
}


int main(){
    LinkList L;        //声明一个指向单链表的指针
    InitList(L);    //初始化一个空表
    // ....后续代码
    
}

5. 指定结点的后插操作

//按位序插入(不带头结点)
#include <iostream>
typedef struct LNode{    // 定义单链表节点类型
    ElemType data;        // 每个节点存放一个数据元素
    struct LNode *next;    // 指针指向下一个节点
}LNode, *LinkList;        // 通过typedef函数,定义的链表和结点别名


// 指定结点的后插操作,  直接把原来插入逻辑解耦了一下
bool  InserNextNode(LNode *p, ElemType e){
    if(p==NULL)    //i的值不合法
    return  false;
    
    // 要在第i-1的结点之后插入一个新的结点
    // 插入逻辑和带头结点的一样,只是加了上面i=1的判断
    LNode *s = (LNode *)malloc(sizeof(LNode));
    s->data = e;
    s->next=p->next;//用s指向后面指针替换了p点指向后面的指针
    p->next=s        //将结点s链接到p之后
    return true;    //插入成功
}

// 在第i个位置插插入元素e(带头结点)
bool ListInsert(LinkList &L, int i ,ElemType e){
    // 找出 p点指针,也就是要插入的位置在位序为第i-1结点
    if(i<1);
        return false;
    if(i==1){    //插入第1个结点的操作与其他结点操作不同
        LNode *s = (LNode *)malloc(sizeof(LNode));
        s->data = e;
        s->next = L;
        L = s;    //头指针指向新结点
        return true;
    }
    LNode *p;    //指针p指向当前扫描到的结点
    int j=1;    //当前p指向的第几个结点
    p = L;        //p指向第1个结点(注意:不是头结点)
    while (p!=NULL && j<i-1){ //循环找到第 i-1个结点
        p=p->next;
        j++;
    }
    return InsertNextNode(p,e);
}


int main(){
    LinkList L;        //声明一个指向单链表的指针
    InitList(L);    //初始化一个空表
    // ....后续代码
    
}

6.指定结点的前插操作

//指定结点的前插操作
#include <iostream>
typedef struct LNode{    // 定义单链表节点类型
    ElemType data;        // 每个节点存放一个数据元素
    struct LNode *next;    // 指针指向下一个节点
}LNode, *LinkList;        // 通过typedef函数,定义的链表和结点别名

//直接写 前插操作逻辑

//前插操作: 在p结点之前插入元素e
bool InsertPrioNode (LNode *p, ElemType e){
    if (p==NULL)
        return false;
    LNode *s = (LNode *)malloc(sizeof(LNode));
    if(s==NULL)         //内存分配失败
        return false;
    s->next = p->next;
    p->next = s;        //新结点s链接到p之后
    s->data = p->data;    //将p中元素复制到s中
    p->data = e;        // p中元素覆盖为e
    return true;        
}

//王道书里面的,直接给穿了  LNode *s
bool InserPriorNode(LNode*p, LNode *s){
    if(p==NULL || s==NULL)
        return false;
    s->next = p->next;
    p->next = s;         // s练到p之后
    ElemType temp = p->next;    //交换数据域部分
    p->data = s->data;
    s-data = temp;
    return true;
    

}

7.按位序删除(带头结点)

//按位序删除(带头结点)
#include <iostream>
typedef struct LNode{    // 定义单链表节点类型
    ElemType data;        // 每个节点存放一个数据元素
    struct LNode *next;    // 指针指向下一个节点
}LNode, *LinkList;        // 通过typedef函数,定义的链表和结点别名

bool ListDelete(LinkList &L, int i , ElemType &e){
    if (i<1)
        return false;
    LNode *p;            // 指针p指向当前扫描到的结点
    int j = 0;            // 当前p指向的第几个结点
    p = L;                // L指向头结点,头结点是0个结点(不存数据)
    while (p!NULL && j<i-1) {    // 循环找到第i-1个结点
        p = p->next;
        j++;
    }
    if(p == NULL)        // i值不合法
        return false;
    if(p->next == NULL)    //第i-1个结点之后已无其他结点
        return false;
    
    LNode *q = p->next;    //令q指向被删除结点
    e = q->data;        // 用e返回元素的值
    p->next = q->next;    //将*q结点从链中"断开"
    free(q);            // 释放结点的存储空间
    return true;        // 删除成功

}

8.指定结点的删除

bool DeleteNode(LNode *p){
    if (p== NUll)
        return false;
    LNode *q = p->next;            // 令q指向*p的后继结点
    p->data = p->next->data;    // 和后继结点交换数据域
    p->next = q->next;            // 将*q结点从链中"断开"
    free(q);                    // 释放后继结点的存储空间
    return true;
}

2020-5-9 21:07:59 先写到这,写了一天代码,感觉还是很充实

2020-5-10 19:08:34上午断网,开始整理

9.按位查找,返回第i个元素(带头结点)

//按位查找,返回第i个元素(带头结点)
LNode*GetElem(LinkList L, int i ){
    if(i<0)
        return NULL;            //输入的值不合法
    LNode *p;                    //指针p当前扫描到的结点
    int j = 0;                    //当前p指向的第几个结点
    p = L;                        //L指向头结点,头结点是第0个结点(不存数据)
    while(p!=NULL && j<i){        //循环找到第i个结点
        p = p->next;
        j++;
    }
    return p;
}

 10.王道书版:按位查找,返回第i个元素(带头结点)

//王道书版:按位查找,返回第i个元素(带头结点)

LNode*GetElem(LinkList L, int i ){
    int j = 1;
    LNode *p = L->next;
    if(i==0)
        return L;                //返回头结点
    if(i<1)
        return NULL;
    while(p!=NULL && j<i){
        p = p->next;
        j++;
    }    
    return p;
}

// 按值查找,找到数据域 ==e 的结点
LNode *LocateElem(LinkList L, ElemType e){
    LNode *p = L->next;
    //从第1个结点开始查找数据域为e的结点
    while (p != NULL && p->data != e)
        p = p->next;
    return p ;                    // 找到后返回该结点指针,否则返回NULL
}

//求表的长度

int Length(LinkList){
    int len = 0;                // 统计表长
    LNode *p = L;
    while (p->next != null){
        p = o->next;
        len++;
    }
    return len;

}

//双链表的初始化(带头结点)

//初始化双链表
typedef struct DNode{
    ElemType  data;
    struct DNode *prior, *next;
}DNode, *DLinklist;


bool InitDLinkList(DLinkList &L){
    L = (DNode *)malloc(sizeof(DNode));        //分配一个头结点
    if(L==NULL)                                // 内存不足,分配失败
        return false;                        
    L->prior = NULL;                        // 头结点的prior永远指向NULL
    L->next = NULL;                            // 头结点之后暂时还没有结点
    return true;        
}
 
// 判断双链表是否为空(带头结点)
bool Empty(DLinklist L){
    if(L->next == NULL)
        return true;
    else
        return false;
}

viod testDLinkList(){
    //初始化双联链表
    DLinkList L;
    InitDLinkList(L);
    // 后续代码
}

// 双链表的后插入操作(按位序插入(就是找到该i-1结点,进行后插),前插操作(找到该结点的前一个结点,进行后插)都是在后插基础上)

// 在p结点之后插入s结点
boo InsertNextDNode(DNode *p, DNode *s){
    if(p==NULL || s==NULL)    //    非法参数
        return false;
    s->next = p ->next;
    if (p->next != NULL)        //如果p结点有后继结点
        p->next->prior = s;
    s->prior = p;
    p->next = s;
    return true;
}

//双链表的删除
// 删除p结点的后继结点
bool DeleteNextDNode(DNode *p){
    if (P==NULL)    
        return false;
    DNode *p = p->next;            //找到p的后继结点q
    if (q->next!=NULL)
        return false;            // p没有后继
    p->next =q->next;    
    if (q->next!=NULL)            //q结点不是最后一个结点
        q->next->prior = p;        
    free(q);                    // 释放结点空间
    return true;    
}

//销毁一个双链表
void DestoryList(DLinklist &L){
    //循环释放各个数据结点
    while(L->next!=NULL)
        DeleteNextDNode(L);
    free(L);                    //释放头结点
    L = NULL;                    //头指针指向NULL
}

//双链表的遍历
//后向遍历
while(p!=NULL){
    //对结点p做相应处理,如打印
    p=p->next;
} 

//向前遍历
while(p!=NULL){
    //对结点p做相应处理,如打印
    p=p->prior;
} 

//向前遍历(跳过头结点)
while(p->prior!=NULL){
    //对结点p做相应处理,如打印
    p=p->prior;
} 

//循环单链表
typedef struct DNode{
    ElemType  data;
    struct DNode *prior, *next;
}DNode, *DLinklist;

//初始化一个循环单链表
bool InitDLinkList(DLinkList &L){
    L = (DNode *)malloc(sizeof(DNode));        //分配一个头结点
    if(L==NULL)                                // 内存不足,分配失败
        return false;                        
    L->next = L;                            // 头结点next指向头结点
    return true;        
}
// 判断循环单链表是否为空
bool Empty(DLinklist L){
    if(L->next == L)
        return true;
    else
        return false;
}
//判断结点p是否为循环单链表的表未结点
bool isTail(LinkList L, LNode *p){
    if (p->next==L)
        return true;
    else
        return false;
}

viod testDLinkList(){
    //初始化双联链表
    DLinkList L;
    InitDLinkList(L);
    // 后续代码
}

//循环单双链表
typedef struct DNode{
    ElemType  data;
    struct DNode *prior, *next;
}DNode, *DLinklist;

//初始化空的循环双链表
bool InitDLinkList(DLinkList &L){
    L = (DNode *)malloc(sizeof(DNode));        //分配一个头结点
    if(L==NULL)                                // 内存不足,分配失败
        return false;                        
    L->prior = L;                            // 头结点prior指向头结点
    L->next = L;                            // 头结点的next指向头结点
    return true;        
}
// 判断循环双链表是否为空
bool Empty(DLinklist L){
    if(L->next == L)
        return true;
    else
        return false;
}
//判断结点p是否为循环双链表的表尾结点
bool isTail(LinkList L, LNode *p){
    if (p->next==L)
        return true;
    else
        return false;
}

viod testDLinkList(){
    //初始化双联链表
    DLinkList L;
    InitDLinkList(L);
    // 后续代码
}

// 双链表的插入
//在p结点之后插入s结点
bool InserNextDNode(DNode *p, DNode *s){
    s->next = p->next;                //将结点*s插入到结点*p之后
    p->next->prior = s;
    s->prior = p;
    p->next = s;
}

// 用代码定义一个静态链表(王道版)
# define MaxSize 10                    //静态链表的最大长度
typedef struct{                        //静态链表结构类型的定义
    ElemType data;                    //存储数据元素
    int next;                        //下一个元素的数组下标
}SLinkList[MaxSize];    

void  testSLinkList(){
    SLinkList a;                    // a是一个静态链表
    // ....后续代码
}

//等价于如下↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
//定义一个静态链表
# define MaxSize 10                    //静态链表的最大长度
struct Node{                        //静态链表结构类型的定义
    ElemType data;                    //存储数据元素
    int next;                        //下一个元素的数组下标
};
// 可用SLinkList定义 "一个长度为MaxSize的Node型数组"
typedef  struct Node SLinkList[MaxSize];        //主要是强调我是一个表,不是数组

void  testSLinkList(){
    struct Node a[MaxSize];            // a是一个Node型数组
    // ....后续代码
}

 2020-5-12 21:43:35

不知不觉更了那么多,小有成就感!

//定义一个栈,初始化操作

#define MaxSize 10;                 //定义栈中元素的最大个数
typedef struct{
    ElemType data[MaxSize];         // 静态数组存放栈中元素
    int top;                        // 栈顶指针
} SqStack;

//初始化栈
viod InitStack(SqStack &S){
    S.top = -1 ;                    //初始化栈顶指针
} 

//判断栈空
bool StackEmpty(SqStack S){
    if(S.top=1);                    // 栈空
        return  true;               
    else
        return false;               // 不空
}

void testStack(){
    SqStack S;                      //声明一个顺序栈(分配空间)
    InitStack(S);                  
    //后续操作  增删改查
}

//进栈操作

#define MaxSize 10;                 //定义栈中元素的最大个数
typedef struct{
    ElemType data[MaxSize];         // 静态数组存放栈中元素
    int top;                        // 栈顶指针
} SqStack;


//新元素入栈
bool Push(SqStack &&S, ElemType x){
    if(S.top==MaxSize-1)            // 栈满,报错
        return false
    S.top = S.top+1                 // 指针先加1
    S.data[S.top] = x;              // 新元素入栈
    //上面两行代码等价于    S.data[++S.top] = x;     ++在前,则是先加,后用
    return  true;
}

// 出栈和读取栈顶元素操作
#define MaxSize 10;                 //定义栈中元素的最大个数
typedef struct{
    ElemType data[MaxSize];         // 静态数组存放栈中元素
    int top;                        // 栈顶指针
} SqStack;

// 出栈
bool Pop(SqStack &S, ElemType &x){
    if(S.top=-1)                   // 栈空,报错
        return false;                
    x = S.data[S.top];              //栈顶元素先出栈
    S.top = S.top -1;               //指针再减1
    //上面两行代码等价于 x = S.data[S.top--];       //先用 后减
    return true;
}

//读取栈顶元素
bool GetTop(SqStack S, ElemType &x){
    if(S.top==1)                    // 栈空,报错
        return false;
    x = S.data[S.top];              // x记录栈顶元素
    return true;                                          
}

// 共享栈
#define MaxSize 10;                 //定义栈中元素的最大个数
typedef struct{
    ElemType data[MaxSize];         // 静态数组存放栈中元素
    int top0;                       // 0号栈栈顶指针
    int top1;                       // 1号栈栈顶指针
} SqStack;

// 初始化栈
void InitStack(ShStack &S){
    S.top0 = -1;                    // 初始化栈顶指针
    S.top1 = MaxSize ;
}

// 栈满的条件   top0 + 1 == top1

//顺序队列

#define MaxSize 10                  //定义队列中元素的最大个数
typedef struct{
    ElemType data[MaxSize];         //用静态数组存放队列元素
    int front , rear;               // 队头指针和对尾指针
}SqQueue;

//初始化队列
void InitQueue(SqQueue &Q){
    //初始时 队列,对尾指针指向0
    Q.rear = Q.front = 0;
}

// 判断队列是否为空
bool QueueEmpty(SqQueue Q){
    if(Q.rear==Q.front)             // 队空条件
        return true;
    else
        return false;
}


void testQueue(){
    // 声明一个队列(顺序存储)
    SqQueue Q;
    InitQueue(Q);
    // 后续操作........
}

//循环队列------- 入队操作
#define MaxSize 10                  //定义队列中元素的最大个数
typedef struct{
    ElemType data[MaxSize];         //用静态数组存放队列元素
    int front , rear;               // 队头指针和对尾指针
}SqQueue;

//判断队列是否为空
bool QueueEmpty(SqQueue Q){
    if(Q.rear==Q.front)             //队空条件
        return true;
    else
        return false;
}

//入队
bool EnQueue(SqQueue &Q, ElemType x){
    if((Q.rear+1)%MaxSize==Q.front)
        return false;               //队满则报错
    Q.data[Q.rear] = x;             // 新元素插入队尾
    Q.rear = (Q.rear+1)%MaxSize;    //队尾指针加1取模(就是取余操作)
    // 用模运算将存储空间在逻辑上变成了"环状"
    return true;
}

// 循环队列---出队

// 出队(删除一个队头元素,并用x返回)
bool DeQueue(SqQueue &Q, ElemType &x){
    if(Q.rear==Q.front)
        return false;               // 队空则报错
    x = Q.data[Q.front];            
    Q.front = (Q.front+1)%MaxSize;  // 队头指针后移
    return true;
}

// 获得队头元素的值,用x返回
bool GetHead(SqQueue Q, ElemType &x){
    if(Q.rear == Q.front)
        return false;               // 队空则报错
    x = Q.data[Q.front];            
    return true;
}

//记住如下内容
# 队列元素个数
(rear+MaxSize-front)%MaxSize

# 以下内容都是: 指向队尾元素的后一个位置(下一个应该是插入位置)
//方案一 : 判断队列已满/已空(浪费空间,其他的2,3方案都不浪费)
#define MaxSize 10                  //定义队列中元素的最大个数
typedef struct{
    ElemType data[MaxSize];         //用静态数组存放队列元素
    int front , rear;               // 队头指针和对尾指针
    // 初始化时 front  rear 都是为0
}SqQueue;

# 队列已满的条件: 队尾指针的再下一个位置是队头
(Q.rear+1)%MaxSize == Q.front

# 队空条件
Q.rear == Q.front

//方案二 : 判断队列已满/已空
#define MaxSize 10                  //定义队列中元素的最大个数
typedef struct{
    ElemType data[MaxSize];         //用静态数组存放队列元素
    int front , rear;               // 队头指针和对尾指针
    int size;                       // 队列当前长度
    // 初始化时 front  rear size 都是为0
}SqQueue;

# 插入成功      size++
# 删除成功      size--

# 队满条件      size==MaxSize
#队空条件       size==0


//方案三  : 判断队列已满/已空
#define MaxSize 10                  //定义队列中元素的最大个数
typedef struct{
    ElemType data[MaxSize];         //用静态数组存放队列元素
    int front , rear;               // 队头指针和对尾指针
    int tag;                       // 最近进行的是删除/插入
    // 初始化时 front=rear=0  tag=0
}SqQueue;

#每次删除操作成功时,都令tag=0;
#每次插入操作成功时,都令tag=1;
//只有删除操作,才可能导致队空
# 队空条件      front==rear && tag==0
//只有插入操作,才可能导致队满
# 队满条件      front==rear && tag==1

//其他出题方法

# 以下都是指向队尾元素(已截图,详情看截图3.5)

如图

 

 

 

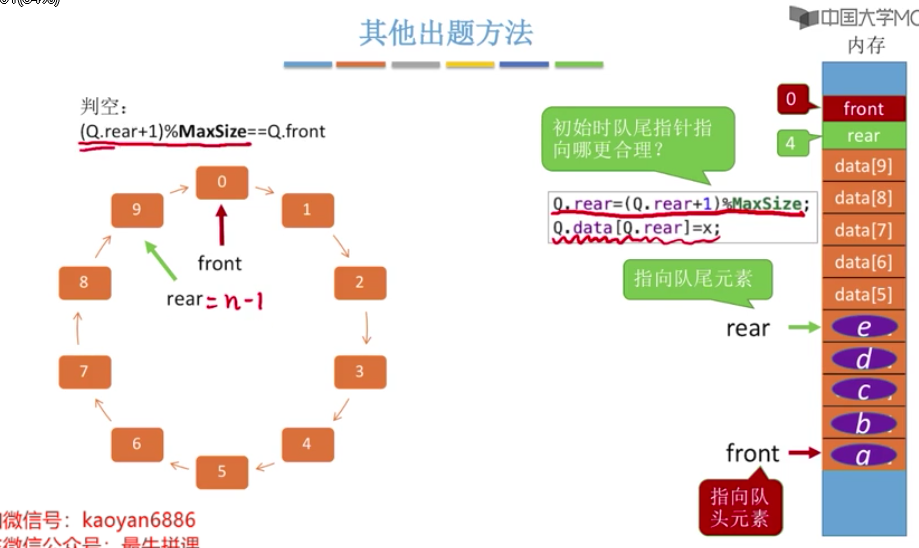
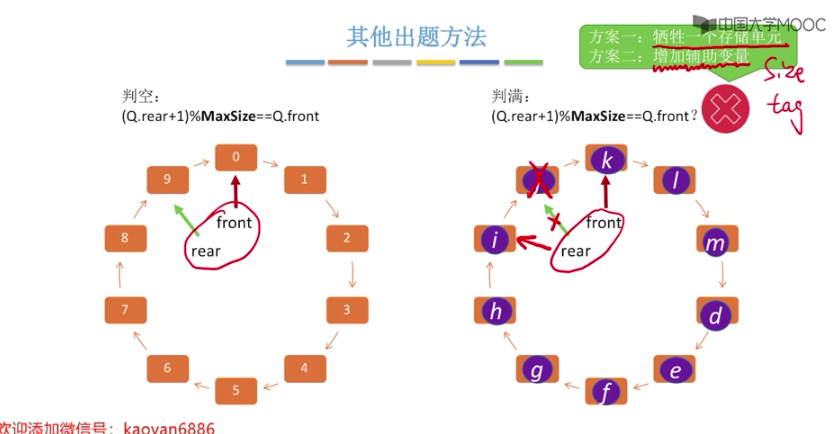
2020-5-12 21:49:23,,明天再看!

 

2020-5-13 18:32:09

2020-5-13 09:41:13(继续干起来)
//队列的连式存储

//初始化(带头结点)
typedef struct LinkNode{
    ElemType data;
    struct LinkNode *next;
}LinkNode;

typedef struct{
    LinkNode *front, *rear;
}LinkQueue;

//初始化(带头结点)
void InitQueue(LinkQueue &Q){
    //初始时 front, rear都指向头结点
    Q.front = Q.rear=(LinkNode*)malloc(sizeof(LinkNode));
    Q.front->next=NULL;
}

//判断队列是否为空
bool IsEmpty(LinkQueue Q){
    if(Q.front=Q.rear)
        return true;
    else
        return false;
}

void testLinkQueue(){
    LinkQueue Q;                    //声明一个队列
    InitQueue(Q);                   // 初始化队列
    //...后续操作.........
}

//################################################
//初始化(不带头结点)

//初始化队列(不带头结点)
void InitQueue(LinkQueue &Q){
    // 初始化 front, rear 都指向NULL
    Q.front = NULL;
    Q.rear = NULL;
}

//判断队列是否为空(不带头结点)
bool IsEmpty(LinkQueue Q){
    if(Q.front==NULL)
        return true;
    else
        return false;
}

//################################################

// 入队(带头结点)
// 新元素入队(带头结点)
void EnQueue(LinkQueue &Q, ElemType x){
    LinkQueue *s = (LinkNode *)malloc(sizeof(LinkNode));
    s->data = x;
    s->next = null;
    Q.rear->next = s;               //新结点插入到rear之后
    Q.rear = s;                     //修改表尾指针
}

// 入队(不带头结点)

//新元素入队(不带头结点)
void EnQueue(LinkQueue &Q, ElemType x){
    LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));
    s->data = x;
    s-next = NULL;
    // 不带头结点的队列,第一个元素入队是哦户需要特别处理 
    if(Q.front == NULL){            // 在空队列中插入第一个元素
        Q.front = s;                // 修改队头队尾指针
        Q.rear = s;
    }else{
        Q.rear->next = s;           //新结点插入到rear结点之后
        Q.rear =s;                  // 修改rear指针
    }
}

//################################################
//出队(带头结点)
//队头元素出队(不带头结点)
bool DeQueue(LinkQueue &Q, ElemType &x){
    if(Q.front==Q.rear)
        return false;               // 空队
    LinkNode *p = Q.front->next;
    x = p->data;                    // 用变量x返回队头元素
    Q.front->next = p->next;        // 修改头结点的next指针
    if(Q.rear==p)                   // 此次是最后一个结点出队
        Q.rear = Q.front;           // 修改rear指针
    free(p);                        // 释放结点空间
    return true;        
}

// 出队(不带头结点)
// 队头元素出队(不带头结点)
bool DeQueue(LinkQueue &Q, ElemType &x){
    if(Q.fron==NULL)
        return false;               // 空队
    LinkNode *p = Q.front;          // p指向此次出队的结点
    x = p->data;                    // 用变量x返回队列元素
    Q.front = p->next;              // 修改front 指针
    if(Q.rear==p){                  //  此次是最后一个结点出队
        Q.front =NULL;              // front 指向 NULL
        Q.rear = NULL;              // rear 指向NULL
    }
    free(P);                        // 释放结点空间
    return  true;           
}
// 链式存储一半不会满,除非内存不足!

//################################################
//栈的应用-----匹配括号算法

// 定义一个栈(可采用链栈,但是考试通常数组即可)
# define MaxSize(10)                // 定义栈中元素的最大个数
typedef struct{
    char data[MaxSize];             // 静态数组存放栈中的元素
    int top;                        // 栈顶指针
}SqStack;

// 考试中可直接使用基本操作,建议简要说明接口

//初始化栈
void InitStack(SqStack &S)

//判断栈是否为空
bool StackEmpty(SqStack S)

// 新元素入栈
bool Push(SqStack &S, char x)

//栈顶元素出栈,用x返回
bool Pop|(SqStack &S, char &x)


bool bracketCheck(char str[], int length){
    SqStack S;
    InitStack(S);                   // 初始化一个栈
    for (int i = 0; i<length; i++){
        if (str[i]=='(' || str[i]=='['||str[i]'{'){
            Push(S, str[i]);        // 扫描到左括号,入栈
        }else{
            if(StackEmpty(S))       // 扫描到右括号,且当前栈空
                return false;       // 匹配失败

            char topElem;
            Pop(S, topElem);        // 栈顶元素出栈
            if(str[i]==')' && topElem !='(')
                return  false;
            if(str[i]==']' && topElem !='[')
                return  false;    
            if(str[i]=='}' && topElem !='{')
                return  false;
        }
    }
    return StackEmpty(S);           // 检索全部括号后,栈空说明匹配成功
}

//################################################

// 一维数组的存储结构
ElemType a[10];                     // 定义一个一维数组

// 定义一个二维数组结构
ElemType b[2] [4];                  // 2行4列的二维数组  

2020-5-22 09:42:23

第四章代码

// 是在看英语难受,,看数据结构

//已经截图 明天再写

// 62020-5-20 22:56:15
// 明天早上5点半起来撸代码
// 已经看完第四章  撸代码

// 串的顺序存储

#define MAXLEN 255              // 预定义最大串长为255
typedef struct{
    // 静态数组实现(定长顺序存储)
    char ch[MAXLEN];            // 每个分量存储一个字符
    int length;                 // 串的实际长度
}SString;


typedef struct{
    // 静态数组实现(堆分配存储)
    char *ch;                   // 按串长分配存储区, ch指向穿的基地址
    int   length;               // 串的长度
}HString;   

HString S;
// 用完需要手动free
S.ch = (char *) mallco(MAXLEN * sizeof(char));


//串的连式存储
// 结合链表的知识考虑优缺点
// 存储密度低,每个字符1B,每个指针4B
typedef struct StringNode{
    char ch;                    //  每个节点存1个字符
    struct StringNode * next;
}StringNode, *StringNode;

// 存储密度提高了
typedef struct StringNode{
    char ch[4];                 // 每个节点存多个字符
    struct StringNode * next;
}StringNode, *Stirng ;


// 基本操作实现
// SubString(&Sub,pos,len):求子串
S.ch = "wangdao";
S.length = 7;

//求子串
bool SubString(SString &Sub, SString S, int pos, int len){
    // 子串范围越界
    if (pos+len-1 > S.length)
        return  false;
    for(int i = pos; i<pos+len; i++)
        Sub.ch[i-pos+1] = S.ch[i];
    Sub.length = len;
    return true;
}


// 比较操作  StrCompare(S, T)

// 比较操作. 若S>T, 则返回值>0;若S=T. 则返回值=0; 若S<T, 则返回值<0

int StrCompare(SString S, SString T){
    for(int i=1; i<=S.length && i<=T.length; i++){
        if(S.ch[i]!=T.ch[i])
            return S.ch[i]-T.ch[i];
    }
    // 扫描过的所有字符都相同.则长度长的串更大
    return S.length-T.length;
}


// 定位操作
// Index(S, T) 定位操作
int Index(SString S, SString T){
    int i = 1, n =StrLength(S), m=StrLength(T);
    SString sub;                // 用于暂存子串
    while(i<=n-m+1){
        SubString (sub, S, i, m);
        if(StrCompare(sub, T)!=0)   ++i;
        else return i;          // 返回子串在主串的位置
    }
    return 0;                   // S中不存在与T相等的子串
} 


// 朴素模式匹配算法
int Index(SString S, SString T){
    int k = 1;
    int i = k, j=1;
    while(i<=S.length && j<T.length){
        if(S.ch[j]=T.ch[j]){
            ++i;
            ++j;                // 继续比较后继字符
        }else{
            k++;
            i=k;
            j=1;
        }
    }
    if(j>T.length)
        return k;
    else
        return 0;
}


// 课本中的朴素模式匹配
int Index(SString S, SString T){
    int i = 1, j=1;
    while(i<=S.length && j<T.length){
        if(S.ch[j]=T.ch[j]){
            ++i;
            ++j;                // 继续比较后继字符
        }else{
            i=i-j+2;
            j=1;                // 指针后退重新开始匹配
        }
    }
    if(j>T.length)
        return i-T.length;
    else
        return 0;
}


// KMP算法代码

int Index_KMP(SString S, SString T, int next[]){
    int i = 1, j =1;
    while(i<=S.length & j<=T.length){
        if(j==0|| S.ch[i]==T.ch[j]){
            ++j;
            ++i;                // 继续比较后继字符
        }
        else
            i=next[j];          // 模式串向右移动
    }
    if(j>T.length)
        return i-T.length;      // 匹配成功
    else
        return 0;
}