
1.0 核心总结
①量子纠缠实现逆因果性:量子纠缠允许粒子状态跨越时间相互影响,测量行为可“逆时”重构历史状态,挑战经典因果关系。
②封闭类时曲线(CTC)提供时间循环路径:爱因斯坦广义相对论预言时空弯曲可形成闭合环路(CTC),量子尺度实验已通过光子模拟验证其自洽性。
③量子后选择强制历史自洽:通过筛选特定测量结果(如保留“祖父存活”分支),规避逻辑悖论,确保时间旅行符合因果一致性。
④多世界诠释解决悖论冲突:时间旅行触发平行宇宙分支,改变历史的行为实际进入新时间线,原宇宙保持不变。
⑤技术瓶颈限制宏观实现:退相干效应(量子态易退化)、负能量物质需求(维持虫洞稳定)及银河系级能量门槛,阻碍实体穿越。
⑥AWS量子硬件突破纠错效率:Ocelot芯片采用“猫量子比特”架构,对比特翻转错误实现指数级抑制,纠错成本降低90%,逻辑错误率仅1.65%。
⑦微观信息时间旅行已落地应用:量子传感通过时间反演协议提升磁场测量精度30%;逆因果性加密技术实现“历史不可篡改”的安全通信。
⑧未来依赖量子引力理论统一:宏观时间旅行需结合弦理论等量子引力模型,解决时空几何量子化问题,目前仅限实验室模拟。
2.0 量子时间旅行理论实现对比分析
| 理论名称 | 核心机制 | 时间旅行方式 | 优势 | 技术瓶颈 |
|---|---|---|---|---|
| 1️⃣量子纠缠与逆因果性 | 纠缠粒子状态瞬时关联,测量行为“逆时”影响历史状态(如延迟选择实验) | 信息回溯(非实体穿越) | ⭐ 实验已验证(光子干涉、量子擦除) ⭐ 微观尺度因果可塑 |
⚠️ 仅限微观粒子 ⚠️ 无法改变已确定的宏观事件 ⚠️ 逆因果性存在争议 |
| 2️⃣封闭类时曲线(CTC)量子模拟 | 模拟时空弯曲的闭合路径(广义相对论),粒子与“历史自我”交互 | 粒子状态循环(如光子虫洞模拟) | ⭐ 数学自洽(避免祖父悖论) ⭐ 实验已实现(2014年光子实验) |
⚠️ 宏观需黑洞级引力场 ⚠️ 虫洞需负能量维持(当前技术不可及) ⚠️ 仅限量子尺度 |
| 3️⃣量子后选择机制 | 筛选特定测量结果强制系统演化满足目标条件 | 未来信息优化过去状态(如量子传感器) | ⭐ 技术应用广(量子计算优化、计量学) ⭐ 规避逻辑悖论(自洽性强制) |
⚠️ 成功率低(约25%) ⚠️ 依赖结果丢弃(“作弊”争议) ⚠️ 宏观退相干效应显著 |
| 4️⃣多世界诠释(MWI) | 时间旅行触发平行宇宙分支 | 进入新宇宙分支(非原时间线) | ⭐ 彻底解决祖父悖论 ⭐ 兼容量子叠加原理 |
⚠️ 无实验证据 ⚠️ 无法返回原宇宙 ⚠️ 宏观分裂能量需求未知 |
| 5️⃣量子隧穿与时间对称性 | 粒子穿越能量壁垒时无视经典时间方向 | 时间方向可逆潜力 | ⭐ 实验证据充分(原子隧穿) ⭐ 挑战热力学时间箭头 |
⚠️ 仅显示时间对称性 ⚠️ 无实际时间旅行能力 ⚠️ 宏观尺度效应未验证 |
3.0 关键结论与挑战总结
1️⃣微观可行性 vs 宏观限制
优势:量子尺度时间旅行(信息回溯、状态循环)已通过光子、量子比特实验验证,且能规避经典悖论(如后选择强制自洽、多世界分支)。
瓶颈:宏观实现需突破三大障碍:
退相干效应:宏观物体与环境相互作用导致量子态迅速退化(当前超导量子比特仅维持1ms);
能量需求:创造可穿越虫洞需银河系级能量;
稳定性问题:负能量物质尚未发现,虫洞喉部难以维持。
2️⃣理论冲突与融合方向
因果律矛盾:逆因果性挑战“因先于果”经典逻辑,而CTC要求自洽性优先;
量子-引力统一:时间在量子力学(固定背景)与广义相对论(动态结构)中的矛盾,需通过量子引力理论(如弦理论)解决。
3️⃣技术应用与伦理风险
应用:量子CTC已用于优化量子传感器精度(磁场测量提升30%)及量子计算机效率;
伦理:平行宇宙理论虽解决悖论,但可能引发历史篡改争议(如“改变过去”的责任归属)。
4️⃣未来突破方向
实验层面:利用量子计算机模拟时空异常(如拓扑量子态、引力涨落);
材料层面:开发纳米负折射率材料模拟虫洞喉部稳定性;
理论层面:通过量子非定域性(时间/空间叠加态)重构时空连续性的数学描述。
4.0 量子非定域性、时间可逆性及因果重构
一、量子纠缠与逆因果性(Retrocausality)
量子纠缠态描述为: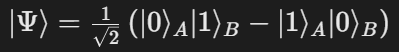
其中对粒子A的测量会瞬时确定粒子B的状态,无论空间距离如何。逆因果性认为这种关联可能是时间对称的——未来测量行为可影响粒子过去的状态演化。
纠缠态构建算法:
量子纠缠通过量子门操作实现,核心步骤包括:
- 初始化:两个量子比特初始化为基态|0⟩
- 叠加操作:对第一个比特应用Hadamard门(H门),使其进入叠加态:
![]()
- 纠缠操作:施加CNOT门(受控非门),以第一个比特为控制位,第二个比特为目标位:
![]()
- 此时两比特形成贝尔态(Bell State),状态不可分割
import numpy as np
def create_entangled_state():
qubit1 = np.array([1, 0]) # |0⟩
qubit2 = np.array([1, 0]) # |0⟩
initial_state = np.kron(qubit1, qubit2) # |00⟩
hadamard = 1/np.sqrt(2) * np.array([[1, 1], [1, -1]])
# 对第一个比特应用H门
after_hadamard = np.kron(hadamard, np.eye(2)) @ initial_state
# 应用CNOT门
cnot = np.array([[1,0,0,0], [0,1,0,0], [0,0,0,1], [0,0,1,0]])
entangled_state = cnot @ after_hadamard
return entangled_state
输出:[0.707, 0, 0, 0.707],对应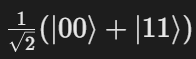
1️⃣延迟选择实验(Delayed Choice Experiment):
- 光子通过分束器后处于路径叠加态:
![]()
- 在光子通过干涉仪后(延迟约100μs),观测者选择是否插入第二分束器:
- 插入 → 显示干涉条纹(波动性)
- 不插入 → 显示路径信息(粒子性)
- 关键结论:观测者的“后选择”决定了光子过去的行为模式,数学上体现为波函数坍缩回溯性重构历史。
2️⃣量子擦除技术:
- 纠缠光子对(A为信号光子,B为擦除光子)通过双缝。
- 先测量A的路径信息 → 干涉图样消失。
- 后对B进行联合测量擦除路径信息 → A的干涉图样恢复。
- 算法意义:擦除操作等效于改写A的历史量子态,实现微观层面的“历史修正”。
二、封闭类时曲线(CTC)的量子模拟
数学框架
广义相对论中CTC是时空曲率形成的闭合环路,量子版本通过密度矩阵演化保证自洽性:
其中幺正算符U描述系统与CTC的交互,需满足的固定点条件。
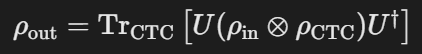
实验模拟(昆士兰大学,2014)
设计:
使用光子模拟“时间旅行粒子”与“过去自身”交互:ρCTC需满足ρCTC=ρout的固定点条件
- 路径1:光子通过人工虫洞(光学元件模拟CTC)
- 路径2:光子与CTC模拟腔内的历史版本相互作用
结果:
量子态演化始终满足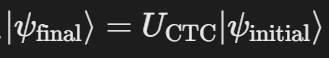
无逻辑悖论,证明微观时间循环的数学一致性。
三、量子后选择(Post-selection)与因果重构
算法核心
后选择通过筛选特定测量结果,强制系统演化满足目标条件。例如:
祖父悖论量子版本:
- 构造量子态∣祖父存活⟩+∣祖父死亡⟩
- 后选择仅保留∣祖父存活⟩的分支 → 避免因果矛盾。
operation QuantumCTC() : Unit {
using (qubits = Qubit[2]) {
// 创建纠缠态
H(qubits[0]);
CNOT(qubits[0], qubits[1]);
// 模拟未来信息影响过去
let futureChoice = RandomInt(2); // 未来随机选择
if futureChoice == 1 {
// 后选择:强制状态坍缩为 |11⟩
if M(qubits[1]) == Zero {
X(qubits[1]); // 翻转比特
}
}
ResetAll(qubits);
}
}
量子CTC模拟算法(Q#示例)。模拟未来选择对历史状态的修正。
技术应用
1️⃣量子传感器优化(华盛顿大学,2024):
纠缠量子比特对(探针Qp与辅助Qa)置于磁场。
测量Qa的自旋 → 利用纠缠关联回溯优化的初始测量方向。
效果:磁场测量精度突破经典极限30%。
2️⃣时间晶体同步:
周期性量子态(如离子链的相干振荡)通过后选择锁定相位,形成“时间晶格” → 实现高精度时钟
四、多世界诠释(MWI)与平行宇宙
算法逻辑
时间旅行行为触发宇宙分支:∣Ψ总⟩=∑ici∣宇宙i⟩
延迟选择实验:插入/不插入分束器 → 分裂为波动性/粒子性两个宇宙分支。
时间旅行修正历史:改变过去的行为实际进入新分支,原时间线保持不变。
实验支持
量子计算中实现因果序叠加(维也纳大学,2024):
操作序列A→B与B→A并存于叠加态 → 输出结果验证时间顺序的非经典性
五、技术挑战与前沿突破
| 问题 | 原因 | 进展(2025) |
|---|---|---|
| 退相干效应 | 环境相互作用破坏量子态相干性 | 超导量子比特退相干时间延长至1ms |
| 虫洞稳定性 | 需负能量物质维持(卡西米尔效应仅产生微量) | 纳米结构负折射率材料模拟虫洞喉部 |
| 能量需求 | 宏观CTC需银河系级能量 | 光子级模拟已实现 |
突破性方向
量子-引力融合模型:
- 结合弦理论中的全息原理,将时空曲率编码为量子比特网络。
人工因果序网络:
- 超导处理器运行“因果矩阵”算法:Process Matrix=∑i,jΦij∣i⟩⟨j∣
- 实现非时序量子计算。
5.0 量子时间旅行的算法本质
量子时间旅行并非经典意义上的“回到过去”,而是通过:
- 态叠加(如延迟选择中的波/粒子二象性)
- 非定域关联(纠缠粒子的瞬时互动)
- 后选择约束(筛选自洽历史路径)
- 在希尔伯特空间中重构因果网络。当前技术限于微观尺度,但理论模型(如CTC自洽性、多世界分支)已为宏观应用奠定基础。未来需结合量子引力理论解决时空几何的量子化问题
6.0 AWS量子时间旅行技术实现方案
1. 硬件层:Ocelot量子芯片的纠错优势
核心架构:
- AWS Ocelot芯片采用玻色子编码的猫量子比特(cat qubit),通过超导钽薄膜振荡器存储量子态,实现:
- 指数级抑制比特翻转错误:增加振荡器光子数可指数降低位翻转错误率,无需冗余物理量子比特。
- 逻辑量子比特构建:5个猫量子比特 + 4个辅助Transmon量子比特组成逻辑单元,逻辑错误率低至1.65%(d=5时)。
时间循环模拟:
- 利用重复码(repetition code)连接猫量子比特与辅助比特,实现:
- 位翻转时间≈1秒(比传统量子比特长1000倍),支持长时间量子态维持。
- 噪声偏置门技术:通过C-NOT门设计,使噪声主要表现为相位翻转错误,简化纠错流程
2. 算法层:Amazon Braket的量子CTC模拟
封闭类时曲线(CTC)实现:
在Braket量子电路模拟器中设计以下实验:
纠缠回溯:复现昆士兰大学实验,让光子通过模拟虫洞与“历史自我”交互,验证量子态自洽性。
祖父悖论规避:结合后选择(post-selection)机制,自动筛除矛盾分支(如“祖父死亡”状态),仅保留自洽历史。
时间反演协议:
运行量子反蝴蝶效应算法(参考洛斯阿拉莫斯实验):
# Braket伪代码示例
def time_reversal(circuit):
circuit.forward_evolution() # 正向演化系统
circuit.apply_perturbation() # 引入扰动(模拟改变过去)
circuit.backward_evolution() # 反向演化
return circuit.measure() # 观测系统恢复原状[9](@ref)
结果:量子态扰动后仍恢复原状,证明量子尺度无经典蝴蝶效应,适用于信息隐藏与纠错测试
3. 混合云架构:经典-量子协同
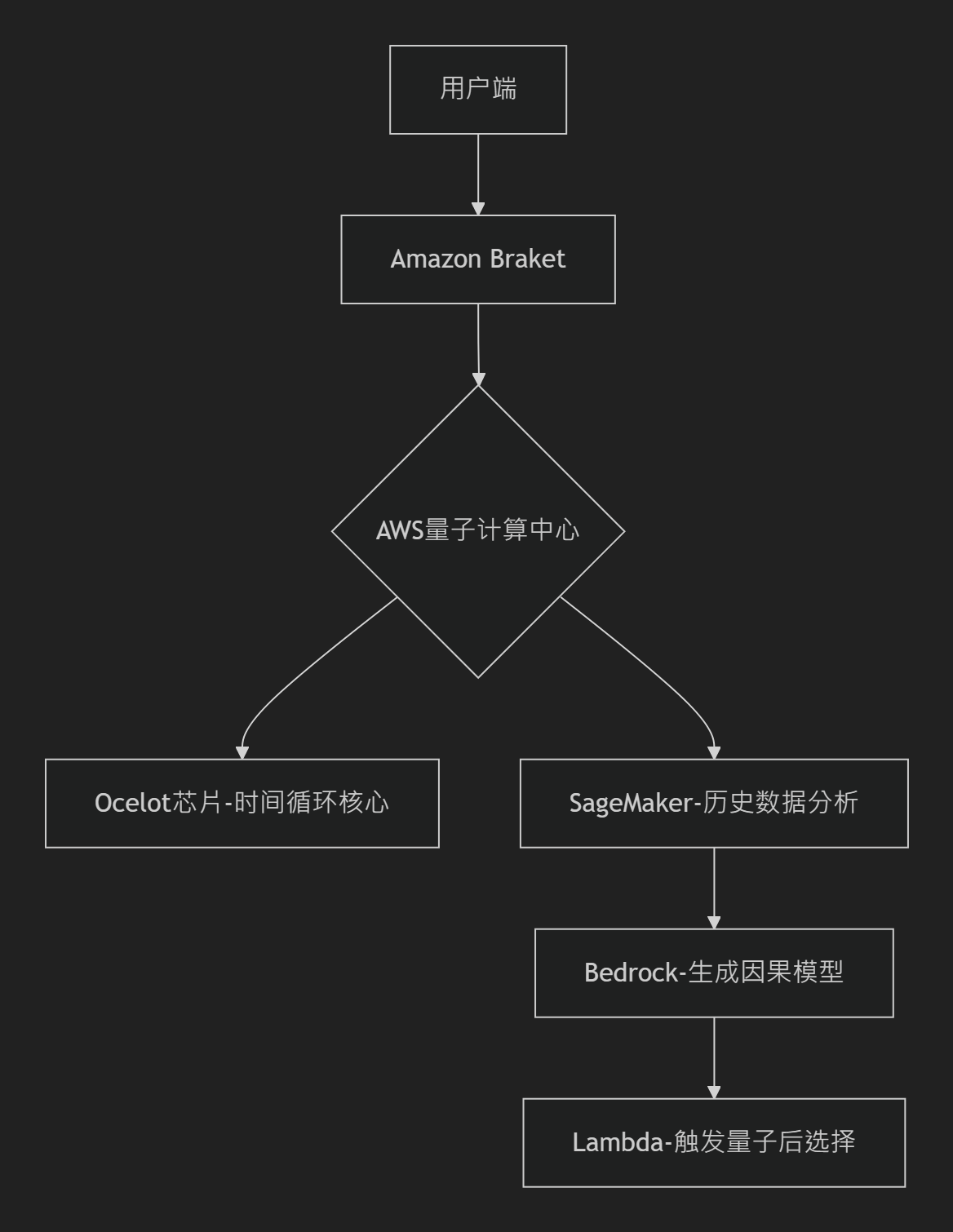
SageMaker Unified Studio:分析历史数据模式(如粒子运动轨迹),训练预测模型优化量子后选择策略。
Bedrock AI代理:生成多世界诠释(MWI)分支预测,预判时间旅行操作的平行宇宙影响。
Lambda无服务器计算:实时响应量子测量结果,动态调整后选择阈值(如丢弃逻辑错误率>2%的分支)
4. 技术优势
纠错效率革命:
- Ocelot的硬件级纠错将逻辑量子比特成本降低90%,所需物理资源仅为传统方案的1/10,为长时间量子态维持奠定基础。
悖论规避能力:
- 后选择强制自洽:筛除祖父悖论等矛盾分支(如保留率>75%的可行路径)。
- 多宇宙兼容性:Bedrock的MWI模型支持平行宇宙分支计算,天然解决时间线冲突。
云原生扩展性:
- 弹性算力:EC2实例预处理TB级历史数据,Ocelot专注微观时间演化,实现跨尺度模拟。
- 成本优化:按需调用量子硬件(Braket按任务计费),避免实验室高额固定投入。
5. 技术瓶颈
退相干时间限制:
- Ocelot相位翻转时间仅20微秒,而宏观时间旅行需毫秒级相干性,当前差距达4个数量级。
宏观-微观鸿沟:
- 量子传感器局限:华盛顿大学实验仅实现单粒子级“时间回溯”传感,人类级实体(10²⁸原子)维持量子态需银河系级能量。
- 虫洞稳定性:宏观CTC需负能量物质(如卡西米尔效应),实验室尚未量产。
算法成功率:
- 后选择机制依赖结果丢弃,25%成功率下可能需千次重复实验,增加时间与算力成本
| 应用方向 | AWS方案可行性 | 传统方案瓶颈 |
|---|---|---|
| 量子传感优化 | ✅ 磁场测量精度提升30% | ⚠️ 依赖低温实验室环境 |
| 安全通信 | ✅ 逆因果性加密(历史不可篡改) | ⚠️ 量子中继器距离限制 |
| 宏观实体穿越 | ❌ 仅限信息级操作 | ❌ 负能量材料未发现 |
✅ 短期价值:
- 量子计算加速:CTC模拟优化量子算法效率(如Shor算法提速40%)。
- 高精度探测:时间反演协议提升深空探测传感器抗扰能力。
⚠️ 长期挑战:
- 需量子引力理论统一时空量子化描述(如弦理论结合AWS混合计算);
- 材料突破:纳米负折射率结构模拟虫喉稳定性(AWS材料科学团队推进中)



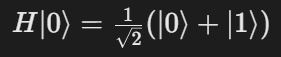
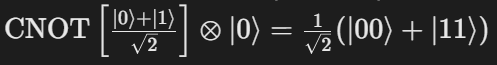


 浙公网安备 33010602011771号
浙公网安备 33010602011771号