堆建立和堆排序
一，堆建立：
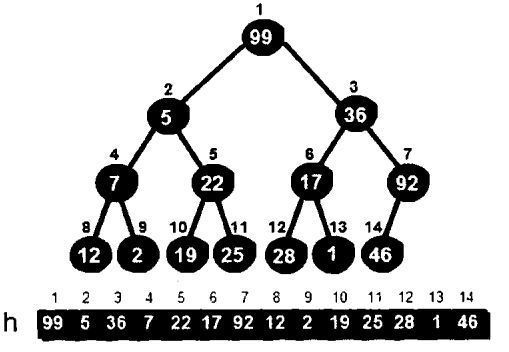
比如说我现在要把这个完全二叉树建立成堆，只要每一个子树都是最小堆就好了，子树也就是一个根节点加上两个子节点。
首先从最后一行来看，最后一行是叶节点，叶节点是没有相应的子节点的，所以所有以叶节点为根结点的子树都是满足最小堆的特性的，所以就直接从叶节点上面一层开始。
现在来看7号结点，发现这个不符合最小堆的特性，所以就要进行交换。后面的4 5 6 7号结点进行同理操作。
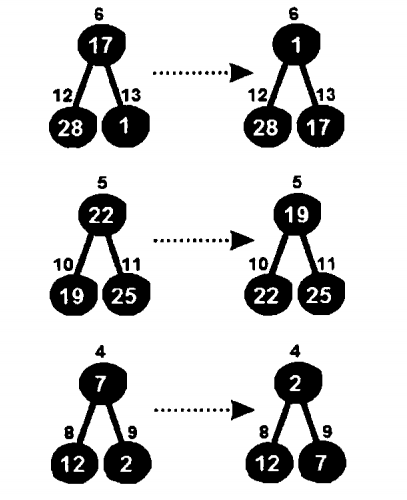
这一层交换完之后就会得到了下面这个二叉树。
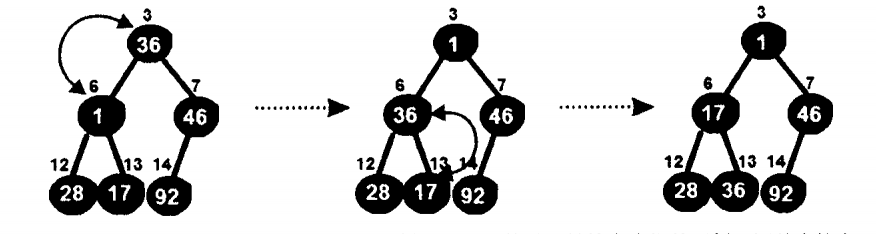
继续对第二层的子树进行同样的操作
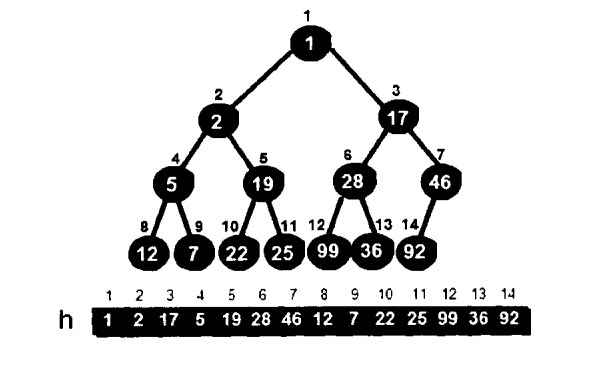
现在就发现已经满足最小堆的特性了！
那么其实做一个总结：就是从叶节点上一层（i = n\2）层 开始一直到第一次进行上面的操作就可以得到最小堆了！
for (i = n / 2; i >= 1; i++) {
siftdown(i);
}
siftdown函数上一篇博客写了，其实代码很简单，只要对这些位置的结点进行向上调整就好了。
二，堆排序：
堆排序的思路其实不会难，假设我们想进行从小到大的排序，可以先建立最小堆，再将顶部元素放入一个新的数组中（顶部元素在堆里面一定是最小的元素），直到堆是空的为止。下面就是怎么删除元素了
1 int deletmin() {
2 int t;
3 t = h[1];//这个就是顶部元素了
4 h[1] = h[n];
5 n--;
6 siftdown(1);
7 return t;
8 }
这个删除函数的思路其实就是为了保证堆的结构，先用一个临时变量记录下第一个顶点的值，然后把最后一个元素的值赋给第一个元素，然后把第一个顶点中的元素向下调整，n的值减一就是把原来最后一个元素给排掉了，最后把一开始记录的t给返回。
1 #include <bits/stdc++.h> 2 int h[101]; 3 int n; 4 using namespace std; 5 int h[100]; 6 void swap(int a, int b) { 7 int t; 8 t = h[a]; 9 h[a] = h[b]; 10 h[b] = t; 11 return; 12 } 13 void siftup(int i) { 14 int flag = 0; 15 if (i == 1) { 16 return; 17 } 18 while (i != 1 && flag == 0) { 19 //判断是否比父节点小 20 if (h[i] < h[i / 2]) 21 swap(i, i / 2); 22 else 23 flag = 1; 24 i = i / 2; 25 26 } 27 return; 28 } 29 30 void creat() { 31 int i; 32 for (i = n / 2; i >= 1; i++) { 33 siftdown(i); 34 } 35 } 36 37 38 //下面就是怎么删除堆中的元素 39 40 void siftdown(int i) { 41 int t, flag = 0; 42 while (i * 2 < n && flag == 0) { 43 if (h[i] > h[i * 2]) { 44 t = i * 2; 45 46 } 47 else { 48 t = i; 49 } 50 //上面其实就是有没有和左结点交换 51 if (i * 2 + 1 <= n) {//也就是存在右结点 52 if (h[t] > h[2 * i + 1]) { 53 t = 2 * i + 1; 54 } 55 } 56 if (t != i) { 57 swap(t, i);//注意这个swap函数存入的是数组的下标 58 i = t;//这个地方下标还是要变的 59 } 60 else { 61 flag = 1; 62 } 63 } 64 return; 65 } 66 67 68 69 int deletmin() { 70 int t; 71 t = h[1];//这个就是顶部元素了 72 h[1] = h[n]; 73 n--; 74 siftdown(1); 75 return t; 76 } 77 78 int main() { 79 int i,num; 80 scanf("%d", &num); 81 for (int i = 1; i <= num; i++) { 82 scanf("%d", &h[i]); 83 } 84 n = num; 85 //这个地方把n重新赋值了 86 creat(); 87 for (int i = 1; i <= num; i++) { 88 printf("%d", deletmin()); 89 90 } 91 92 return 0; 93 }
其实堆排序还有更简单的方法：之前的方法是建立最小堆，把堆顶元素拿出来放到一个数组里面，然后把最后一个结点中的元素放到堆顶，然后向下调整来保持堆的特性。而下面这种方法是要建立最大堆的，比如我现在想要从小到大排序，希望最大的放在后面，所以我就把第一个元素和最后一个元素交换。交换后向下调整依次来保证堆的特性。
1 void headsort() {
2 while (n > 1) {
3 swap(1, n);
4 n--;
5 siftdown();
6 }
7 return;
8 }
最后来进行一个总结：支持插入元素和寻找最大最小元素的数据结构被称为优先队列，如果普通队列像要实现这样的功能就要枚举整个队列，这样时间复杂度很高。
但是如果要学会用堆排序以及堆来解决问题对我来说还有很长的路要走。
参考《啊哈算法》