树,二叉树,堆
一,树:
1,树的简单介绍:
首先我们先来看下面这个图:
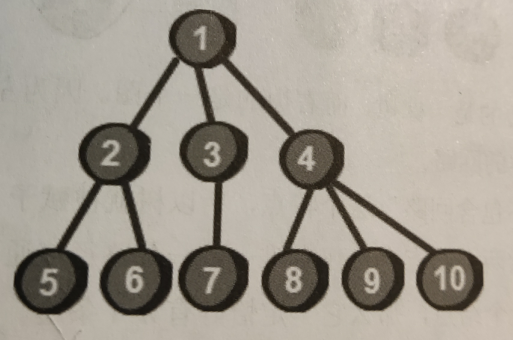
欸??这个不就是之前说的图么?和树有啥关系呢,其实可以把这个图倒过来看,不就像一颗树了么!哈哈哈!那么重要的问题来了,树和图有说明区别呢?
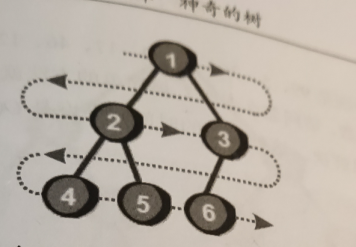
树其实是不包含回路的连通无向图,看下面两个图的区别

图一是一个树,而图二却不是一个树,因为图二很明显是包含一个1->2->5->3->1这样一个回路,所以 图二不是一个树。
下面是树的特性:
1.一棵树中的任意两个结点有且仅有唯一的路径相连
2.如果这个树有n个结点,则它一定恰好有n-1条边
3.在一棵树中加一条边会构成一个回路
后面为了方便文章的展开在这里做一些解释:

首先每一个树的最上方的结点称为根,一个树只有一个根结点。下面再定义一下父节点和子节点,比如说2号结点,它是1号结点的子节点,也是4号和5号结点的父节点。如果一个结点没有子节点那么就称为叶结点,也就是这个树最上面的一层,在这个图里是4,5,6,7号结点。每一个结点有其相应的深度,也就是这个上面每个结点的数字。其实整体还是比较好理解的qwq。
2,二叉树:
二叉树也是树的一种特殊情况,其实也就是每一个父节点只有两个儿子。假设这个地方就把左结点叫做左儿子,右结点叫做右儿子吧。更加严格的递归定义(说实话看不是很懂):二叉树要么为空,要么由根结点,左子树,右子树组成,而左子树和右子树分别是一棵二叉树,如下图:
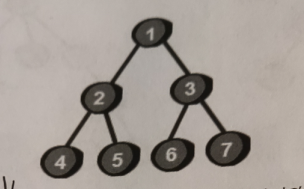
二叉树还有两种特殊的二叉树,叫做满二叉树和完全二叉树。如果二叉树中每一个根结点上都有两个子结点的话,那么这就叫做满二叉树。二叉树的严格定义其实就是:一棵深度为n,且有2^n-1个结点的二叉树。图如下:
如果一个二叉树除了最右边缺少几个叶节点的话,其他都是满的,这样的二叉树其实就是完全二叉树。
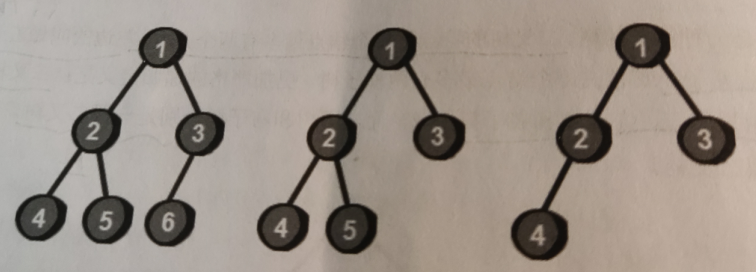
认真对比上面三个图,其实不难发现就是右下角少了一小块。这个就是完全二叉树。
后面让我们描述一下完全二叉树的一些特点吧:
从编号来看如果一个完全二叉树的父节点编号为k,那么他的左节点就是2*k,右结点就是2*k+1。如果已知儿子(无论左右)的编号是x那么父节点的编号就是x/2,如果一个完全二叉树有N个结点,那么高度就是log2N+1,完全二叉树的典型运用就是堆,下面让我们来介绍堆吧。
二,堆:
1,堆的简单介绍:

看这个图,发现了一个父节点的两个子结点都比父节点小,这样的完全二叉树称为最小堆那么反之就是最大堆。
2,堆的用处:
假如现在有14个数,99、5、36、7、22、17、46、12、2、19、25、28、1和92,现在清找出这些数中的最小值,很简单只要遍历储存这些数的数组然后不停的进行代换就好了,但是我们有更好的办法么?如果我们想要删除其中的最小值再新增一个数23,然后再次求这些数中的最小值呢?这里就要用到堆这种数据结构了。
现在让我们把这14个数按照最小堆的方式排列,放入一个完全二叉树:
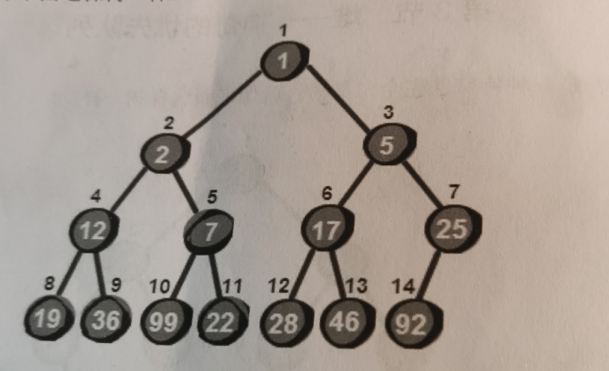
假设储存这个堆的数组是h:

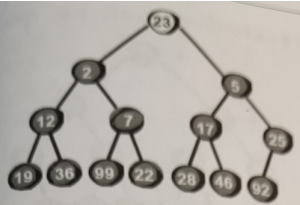
堆顶的数很明显最小,这个最小的数也就是h[1],现在把堆顶删除,然后把原来的23放在堆顶:
现在把23和它的两个儿子2和5来进行比较,选择其中较小的一个数和它交换那么一直重复这个过程就会得到下面这个图:
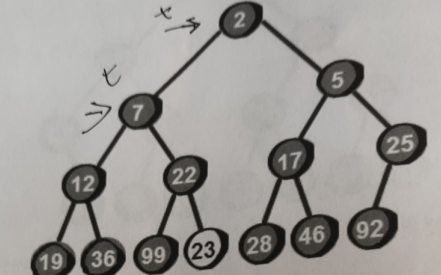
现在就符合最小堆的性质了
1 //向下调整函数值,传入一个需要调整的节点编号i
2 void siftdown(int i) {
3 int t, flag = 0;//传入一个需要向下调整结点编号,这里传入1,就是从heal的顶点开始向下调整。
4 //flag = 0是用来判断是否要继续向下调整
5 //当i结点有儿子的时候(至少要有左儿子)并且还要继续向下调整的时候。
6 while (i * 2 <= n && flag == 0) {//这个判断条件说明这个结点不是最后一层结点(左结点的编号是父节点的两倍)
7 //首先要先判断它和左儿子的关系,并用t记录较小结点的编号
8 if (h[i] > h[i * 2]) {
9 t = i * 2;
10 }
11 else
12 t = i;
13 }
//上面的一段代码其实只是为了判断左儿子是不是要交换,所以只是t的值发生变化
14 if (i * 2 + 1 <= n) {//这个完全二叉树还没有到叶节点的地方
15 if (h[t] > h[t * 2 + 1]) {
16 t = i * 2 + 1;
17 }
18 //只要发现最小编号不是自己,说明子节点中有比父结点小的值存在
19 if (t != i) {//换句话说就是经过交换了
20 swap(t, i);
21 i = t;//现在原来的那个t就变成了起始的位置
22 }
23 else {
24 flag = 1;//这里就说明当前的父节点已经比两个子节点都要小了,不需要再进行调整了
25 }
26 return;
27
28 }
29 }
总之,总结一下就是在左结点不是最后的的叶节点的时候,循环往下,先判断左节点和父节点的大小,如果未交换则判断父节点与右节点的大小,如果左节点大于父节点,交换后还需要比较左节点与右节点的大小。然后因为前面记录的全部都是下标,所以把之前的下标和现在的下标进行对比,如果下标不一样就继续往下换,如果下标是一样的话,就停止交换。
上面说的是怎么将堆中的元素往下调整,后面就是怎么把堆中的元素往上调整了
1 void siftup(int i) {
2 int flag = 0;
3 if (i == 1) {//如果是堆顶就不需要继续了
4 return;
5 }
6 while (i != 1 && flag == 0) {
7 //判断是否比父节点小
8 if (h[i] < h[i / 2])
9 swap(i, i / 2);
10 else
11 flag = 1;
12 i = i / 2;
13
14 }
15 return;
16 }
其实向上调整会简单很多,因为只要子节点和他相应的父节点来比较就好了,不需要进行两个子结点之间的比较。
之前说了那么多的在堆中移动元素但是怎么建立一个堆呢??
n = 0;
for (int i = 0; i < n; i++) {
n++;
h[n] = a[i];
siftup(n);
//其实就是从空的堆开始,依次往堆中插入元素
}
参考书籍:《啊哈算法》



 浙公网安备 33010602011771号
浙公网安备 33010602011771号