最短路径

最短路径问题

一，Floyd-Warshall算法

1，简单介绍：

　　

阮阮看见寒假近在眼前他迫不及待的开始准备他的寒假出行计划。他打算去一写城市旅行，有些城市之间有航线，有些城市之间没有，阮阮为了
省钱所以他想要知道任意两个城市之间的最短路径那么精通编程的他要怎么办呢？

这个问题也被称为“多源最短路径问题”，首先肯定是需要把各个城市之间的航线给储存起来，我们上次的博客有提到了邻接矩阵存储法，那么这个地方也是一样用这个方法来储存：我们用一个4*4的矩阵来储存

                                                                                                          

 

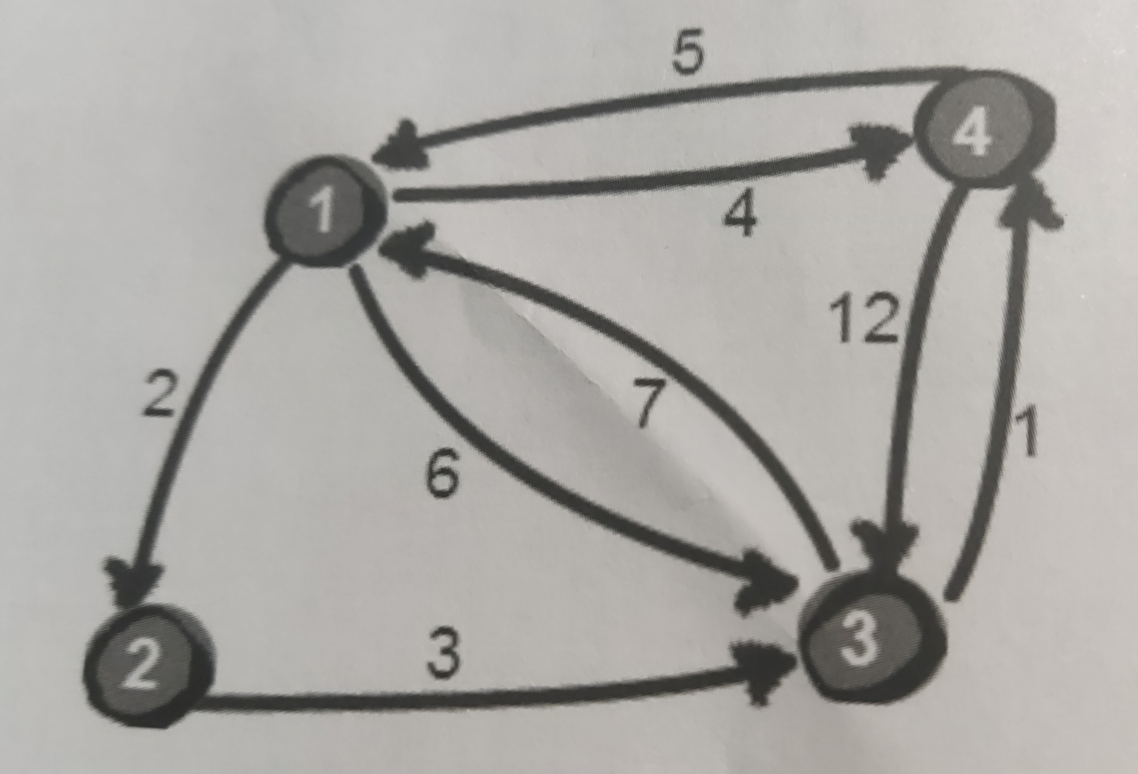
　　现在就是要把这个很复杂的玩意给储存到一个二维数组中去。从这个图里可以看出来，1号城市到2号城市的距离是2，所以说e[1][2] = 2，如果这个城市没法到另外一个城市就把他们之间的距离设置为0.那么这里又是最短路径问题，其实用深度优先搜索和广度优先搜索其实也可以解决但是这次用一个新方法。从a城市到b城市在中间引入另外一个城市最为中转站，原来是a->b，现在变成了a->k->b，只有这样才可能尽量缩短路程。这里举一个例子，假设从4号城市到三号城市一开始是12的路程，现在从4->1->3来看以1为中转点的话，那么这里的路程就变成11也就是e[4][1]+e[1][3]把原来的e[4][3]。同理如果这里通过2个城市来进行中转的话如1号和2号城市，那么这个给距离就会变成10，所以每一个顶点都有可能会使两个顶点之间的距离变短。这里假设任意两点之间不能通过第三个点，一开始的路程就是最短距离。现在假设只允许经过1号顶点。现在其实就是要比价e[i][j]与e[i][1]+e[1][j]。这其实就说明从  i 号城市到1号城市再到  j  号城市。

for(i = 1;i<=n;i++){
    for(j = 1;j<=n;j++){
        if(e[i][j]>e[i][1]+e[1][j]){
            e[i][j]>e[i][1]+e[1][j];
        }
    }
}

　现在呢最短路程就发生了变化，变化如下：

 

那么其实别的点也是一样的，所以这个地方就是设计一个循环表示允许不同的点作为中转。这样就会让这个图上的路径不断的更新。最后不断的更新完之后得到这个图；

 

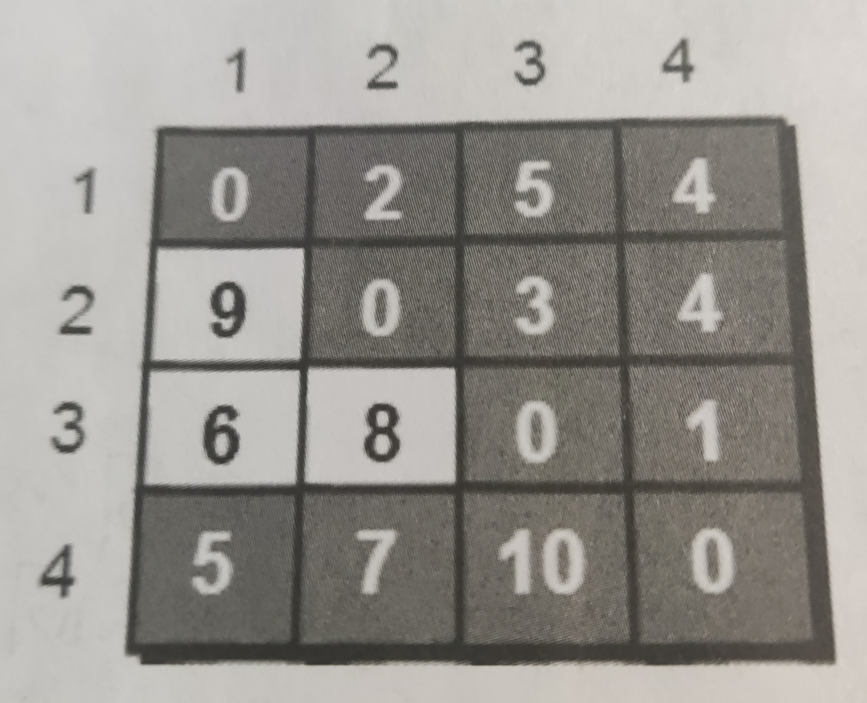
现在所有位置储存的都是最短路径了，所以下面上代码吧

 二，代码实现

#include <stdio.h>
int main() {
    int e[10][10], k, i, j, n, m, t1, t2, t3;
    int inf = 99999999;//这个地方我们认为是正无穷值
    scanf_s("%d %d", &n, &m);
　　　　//邻接矩阵存储法的初始化，也就是读入初始数值
    for (i = 1; i <= n; i++) {
        for (j = 1; j <= n; j++) {
            if (i == j) {
                e[i][j] = 1;
            }
            else {
                e[i][j] = inf;
            }
        }
    }
    //读入边
    for (i = 1; i <= m; i++) {
        scanf_s("%d %d %d", &t1, &t2, &t3);
        e[t1][t2] = t3;
    }

    //后面就是floyd-warshall的核心算法
    for (k = 1; k <= n; k++) {//这里就是进行之前所说过的要通过遍历所有中转站
        for (i = 1; i <= n; i++) {
            for (j = 1; j <= n; j++) {
                if (e[i][j] > e[i][k] + e[k][j]) {
                    e[i][j] = e[i][k] + e[k][j];//这里的k其实就是中转站
                }
            }
        }
    }
    for (i = 1; i <= n; i++) {
        for (j = 1; j <= n; j++) {
            printf("%d", e[i][j]);
        }
        printf("\n");
    }
    return 0;
}

其实写到这会发现这个Floyd-Warshall算法的核心算法只有5行，所以其实是一个比较容易实现的算法，还有就是如果这个图带有负权边，这个算法也可以使用，但是如果遇到负权环的话，最短路径会不停的减1

就永远找不到最短路径。　　

二，Dijkstra算法

1，简单介绍：

之前的Floyd-Warshall是用来处理多源最短路径的问题，也就是最后得到的是各个顶点之间的最短路径。而现在要指定一个点到其余点的最短距离，假设这个点是1，现在要求这个点到其他点的距离最小值：

 

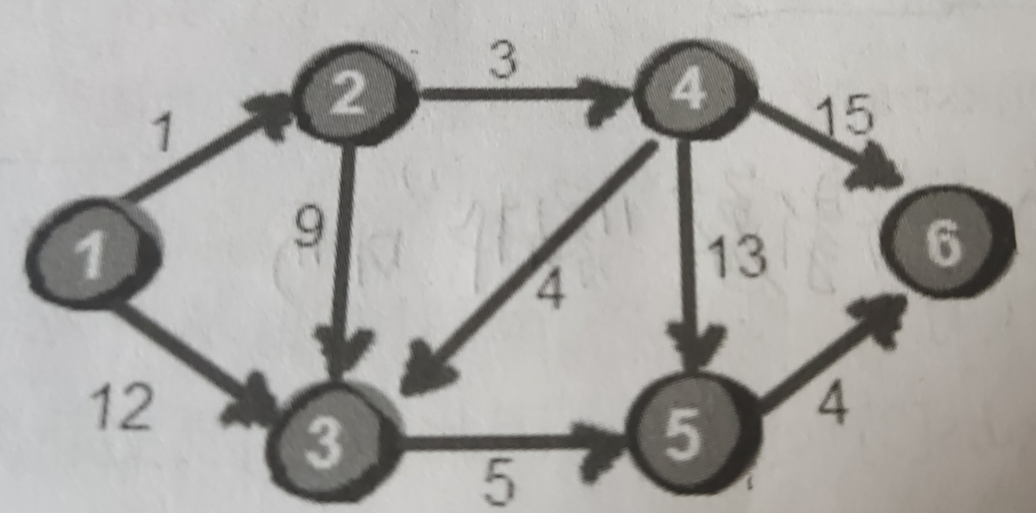
首先还是用邻接矩阵存储法来进行储存：

 

这里在引入一个dis数组来进行储存1到各个顶点的最短距离，首先他们之间的初始路程就是距离

 

有与1相连的就把距离设为他们间的距离，没有与1相连的就把相应的标号设置为无穷。现在这个数组里面的值都是“估计值”。现在先找一个距离1最小值，dis数组中有和1相连且距离最短的不就是2嘛，所以说1到2的最小值就是dis[2]里面所储存的值。在这个图中，所有值都是正数，2已经是距离1的距离最短了，总不能再经过某个中转点使得值变得更小吧，所以现在这个估计值变成了确定值。现在从2号顶点出发，2到3，和2到4两条路。首先1本身有和3相连，所以现在就是要判断1到2，2再到3，会不会使得1到3的距离变短呢？那么现在就是要判断dis[3]和dis[2]+e[2][3]的值的大小，然后发现dis[2]+e[2][3]的值是小于dis[3],所以dis[3]的值就进行了更新，这个操作叫做松弛。同理dis[4] 与 dis[2]+e[2][4]，然后使dis[4]的值进行松弛。然后再来选择一个没有松弛过的点，也就是在3，4，5，6中选择一个理1最近的点，也就是在3和4里面选择一个数，选择选择4这个点（4->3,4->5,4->6）,在来进行上述的松弛，再从3，5，6这些没有进行松弛过的点松弛，然后以此类推。那么所有松弛都完毕之后这个数组变成了：

 

2，代码实现：

#include <stdio.h>
int main() {
    int e[10][10], dis[10], book[10], i, j, n, m, t1, t2, t3, y, v, min, u;

    int inf = 99999999;
    scanf_s("%d %d", &n, &m);
    for (i = 1; i <= n; i++) {
        for (j = 1; i <= n; j++) {
            if (i == j) {
                e[i][j] = 0;
            }else{
                e[i][j] = inf;
            }
        }
    }
    for (i = 1; i <= m; i++) {
        scanf_s("%d %d %d", &t1, &t2, &t3);
        e[t1][t2] = t3;
    }
    //后面就是dis数组的初始化
    for (i = 1; i <= n; i++) {
        dis[i] = e[1][i];
    }
    //book数组的初始化，用来记录这个点是否已经进行了松弛
    for (i = 1; i <= n; i++) {
        book[i] = 0;
    }
    book[1] = 1;
    //后面就是Dijkstra算法的核心
    for (i = 1; i <= n - 1; i++) {
        //后面就是找离1号顶点最近的点，其实也就是找dis数组里的最小值
        min = inf;
        for (j = 1; j <= n; j++) {
            min = dis[j];
            u = j;//把这个点的位置给记录下来
        }
        book[u] = 1;//一定是之前的最短路径往上加，已经排好序的位置往上加，这里其实就是最短的位置
    }
    for (v = 1; v <= n; v++) {
        if (dis[v] != inf) {//首先这个值不能是无穷，因为说明这个值没有和1相连
            if (dis[v] > dis[u] + e[u][v]) {
                dis[v] = dis[u] + e[u][v];//这个u其实就是之前的最小位置。
            }
        }
    }
    for (i = 1; i <= n; i++) {
        printf("%d ", dis[i]);
    }
    return 0;
}

我后面去了解了一下，发现这个也是一种贪心的思想（我还没有学贪心算法）而且这个算法是不能处理负权边，就是每次都要找出起点到所有点的距离的最小值。能处理负权边的

 

三，Bellman-Ford算法

1，简单介绍：

之前的算法并不能解决负权边问题（不是负权回路），而Bellman-Ford算法可以解决这个问题。先写一下这个算法的核心代码：

for (k = 1; k <= n - 1; k++) {
    for (i = 1; i <= m; i++) {
        if (dis[v[i]] > dis[u[v]] + w[i]) {
            dis[v[i]] = dis[u[v]] + w[i];
        }
    }
}

这里就是用邻接表来储存数据了，这个外循环进行了n-1次（n是顶点的个数），内循环循环了m次（m是边的数量）。dis数组还是用来记录源点和各个顶点的距离（dis(u[i])），3个数组的作用是用来储存边的信息。看看从从u[i]->v[i]的距离使得1号顶点到v[i]的距离变短。这个其实也就是上面所说的松弛。现在我要让每一条边都松弛一遍。

 

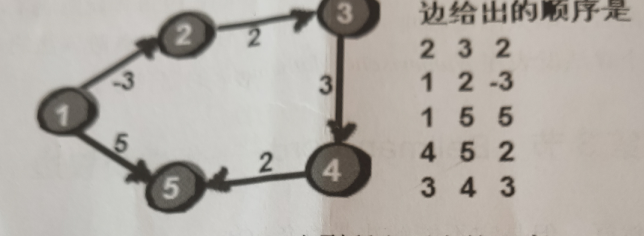
首先先处理2 3 2，首先将dis[3]的值和dis[2]+w[1]，dis[2]是无穷，所以显然不行使dis[3]变小，松弛失败了。现在我就要将所有边都进行一边松弛：

 

松弛之后发现，一号顶点到2号和5号的距离变短了，而看右边的图就可以知道2和5其实就是和1相连的第一条边然后进行第二轮松弛：

 

 

 

 

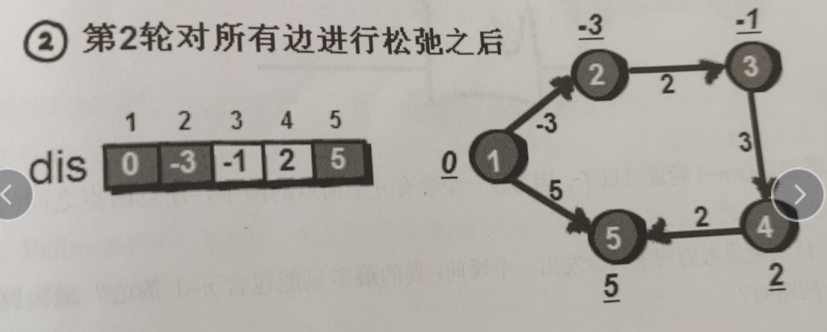
现在就是距离1号顶点的第2条边发生了松弛.所以这里其实就是可以总结出一个结论：第n轮的松弛，松弛的是距离1号源点的第n条边。 现在有一个问题就是为什么是进行n-1轮。因为在一个含有n个顶点的图中两个顶点最短路径只有n-1个。但是有一个问题，如果包含回路呢？？其实是不会有回路。

 

回路有两种，一种是正权回路（权值和为正，也就是所有路程加起来是正的），一种是负权回路（与正权回路同理）。如果去掉正权回路，那么就一定会有路径最小值（我还不理解这个），还有就是负权回路，每一次经过一次负权回路，路径都会变短所以更不可能存在了。

 

 

 

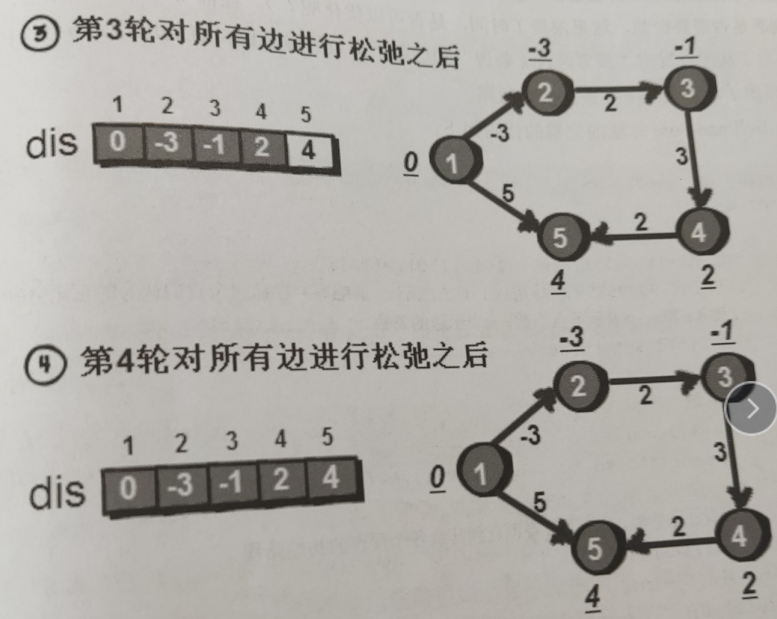
发现了没有，第三轮和第四轮的dis数组没有发生任何的变化，这里可不可以进行一个优化呢？这个问题留到后面下面先来看一下完整的代码实现：

 

#include <stdio.h>
int main() {
    int dis[10], i, k, n, m, u[10], v[10], w[10];
    int inf = 99999999;
    scanf_s("%d %d", &n, &m);//n个顶点，m个边
    //读入边
    for (i = 1; i <= m; i++)
    {
        scanf_s("%d %d %d", &u[i], &v[i], &w[i]);
    }
    //初始化dis数组
    for (i = 1; i <= n; i++) {
        dis[i] = inf;
    }
    dis[1] = 0;
    //bellman——ford算法核心语句
    for (k = 1; k <= n - 1; k++) {
        for (i = 1; i <= m; i++) {
            if (dis[v[i]] > dis[u[i]] + w[i]) {
                dis[v[i]] > dis[u[i]] + w[i];
            }
        }
    }
    for (i = 1; i <= n; i++) {
        printf("%d ", dis[i]);
    }
    return 0;
}

 

刚刚有提到过，这个算法是无法处理负权回路的，所以这个算法是可以用来判断是否会构成负权回路，思路就是在进行了n-1次的循环后按理来说已经找完了最短路径了，后面再进行循环dis数组就不会发生变化。但是如果还会发生变化的话，就说明有负权回路。那么来看看这一段的代码实现。

//用bellman——ford算法来检测是否有负权回路
for (k = 1; k <= n - 1; k++) {
    for (i = 1; i <= m; i++) {
        if (dis[v[i]] > dis[u[i]] + w[i]) {
            dis[v[i]] = dis[u[i]] + w[i]；
        }
    }
}
int flag = 0;
//就是在进行了n-1次的循环之后按理来说就全部都是最短路径了，但是发现还能变得更小所以，这个就说明是有负权回路的情况

for (i = 1; i <= m; i++) {
    if (dis[v[i]] > dis[u[i]] + w[i]) {
        flag = 1;//flag是1的话就说明有负权回路
    }
}

那么之前有说过是否在已经找到所有最短路径后还会进行一次判断，这里其实就浪费了一个判断的时间所以这里还可以进行一个优化：

bellman--ford的算法优化这个就是完整的了
#include  <stdio.h>
int main() {
    int dis[10], ba[10], i, k, n, m, u[10], v[10], w[10],check,flag;
    int inf = 99999999;
    scanf_s("%d $d", &n, &m);
    for (i = 1; i <= m; i++) {
        scanf_s("%d %d %d", &u[i], &v[i], &w[i]);
        
    }
    //初始化dis数组
    for (i = 1; i <= n; i++) {
        dis[i] = inf;
    }
    dis[1] = 0;
    //后面就是核心语句了
    for (k = 1; k <= n - 1; k++) {
        check = 0;//本轮dis数组是否发生更新。
        for (i = 1; i <= m; i++) {
            if (dis[v[i]] > dis[u[i]] + w[i]) {//这里有一个问题就是有时候在松弛之后就已经是最短了，但是还是需要判断这里浪费了时间
                dis[v[i]] > dis[u[i]] + w[i];
                check = 1;
            }
            if (check = 0) {
                break;
            }
        }
    }
    //检查负权回路
    flag = 0;
    if (dis[v[i]] > dis[u[i]] + w[i]) {
        //        flag = 1
    }
    if (flag == 1) printf("有负权回路");
    else {
        for (i = 1; i <= n; i++) {
            printf("%d", dis[i]);
        }
    }
    return 0;
}

 

 

 那么这里好像已经是比较完整的最短路径的算法了

 

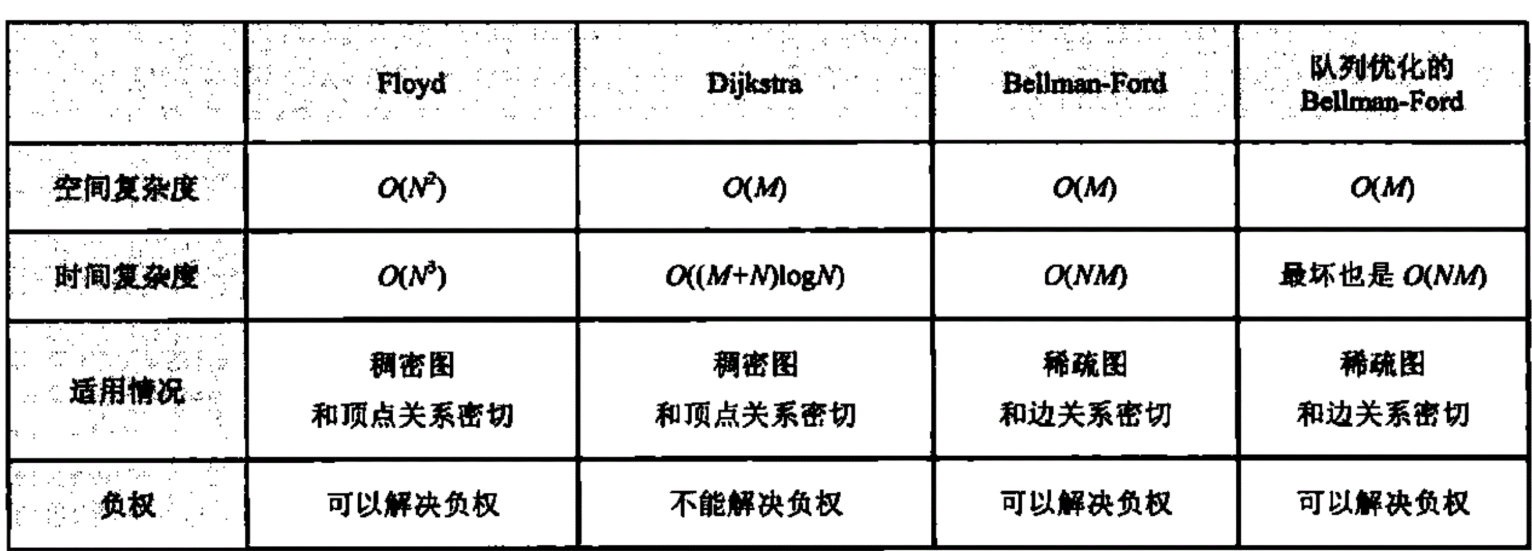
 这就是不同算法之间的选择与差别，然后呢队列优化后面再来说吧，我对于邻接表还不是很熟。

参考书籍：《啊哈算法》