动态规划

通过组合子问题来解决问题，各个子问题不独立，子问题包含公共子问题，每个子问题求解一次将结果保存在表中

1：描述最优解结构

2：定义递归的最优解

3：自底向上求解最优解的值

4：根据每步的计算结果构造最优解

 

适用动态规划的两个基本要素：

1：最优子结构：当问题最优解中包含子问题的最优解

2：重叠子问题

 

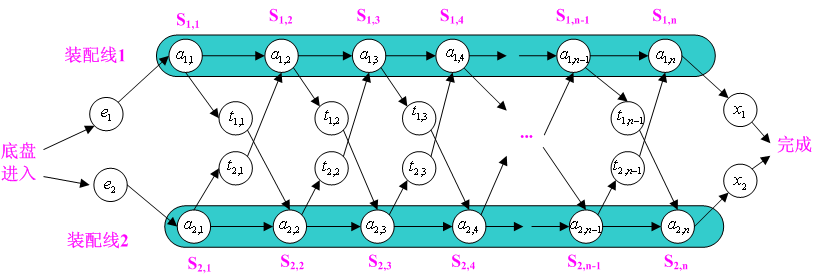
我们令fi[j]为底盘到Si,j的最优解i=0,1 j=1....n

问题最优解：f* = min(f1[n]+x1,f2[n]+x2)

f1[j] = min(f1[j-1]+a1,j-1,f2[j-1]+t2,j-1+a2,j-1)  2<=j<=n

f1[1] = e1 + a11

f2[j] = min(f2[j-1]+a2,j-1,f1[j-1]+t1,j-1+a1,j-1)  2<=j<=n

f2[1] = e2 + a21

其中f1[j-1]、f2[j-1]为最优解，包含最优子结构

包含重叠子问题：比如f1[n]和f2[n]都会对f1[n-1]和f2[n-1]求解符合动态规划的两个基本要素。

a = [[7,9,3,4,8,4],[8,5,6,4,5,7]]
t = [[2,3,1,3,4],[2,1,2,2,1]]
e = [2,4]
x = [3,2]
f1 = []
f2 = []
def Fastest_way(a,t,e,x,n):

    f1.append(a[0][0]+e[0])
    f2.append(a[1][0]+e[1])
    for index in range(1,n):
        temp1 = f1[index-1] + a[0][index]
        temp2 = f2[index-1] + t[1][index-1] + a[0][index]
        if temp1 < temp2:
            f1.append(temp1)
        else:
            f1.append(temp2)
            
        temp1 = f2[index-1] + a[1][index]
        temp2 = f1[index-1] + t[0][index-1] + a[1][index]
        if temp1 < temp2:
            f2.append(temp1)
        else:
            f2.append(temp2)

    return min(f1[n-1]+x[0],f2[n-1]+x[1])

print (Fastest_way(a,t,e,x,len(a[0])))
for i in f1:
    print(i)
for i in f2:
    print(i)

http://www.cnblogs.com/Anker/archive/2013/03/09/2951785.html