【RegNet】2020-CVPR-Designing Network Design Spaces-论文阅读
Designing Network Design Spaces
2020-CVPR-Designing Network Design Spaces
来源:ChenBong 博客园
- Institute:FAIR
- Author:Ilija Radosavovic、Kaiming He
- GitHub:
- Citation:10+
介绍
本文运用统计学的角度,手动从大到小逐渐约束模型的设计空间,从而找到一个好的模型设计空间。
动机
为什么有了这么多好的NAS算法,还需要精心手动设计搜索空间呢?
因为目前的NAS算法大多都是 focus 在 “个体估计” 层面。即 在一个搜索空间里,每次采样和评估都是以个体为单位,最终目的是找到一个或几个最好的结构。
这就带来了几个问题:
- 搜索空间先验性太强。 网络结构搜索应该由2部分内容,即搜索空间的设计和空间内搜索算法。现有的NAS paper主要是在搜索算法上的探索,而对搜索结果影响很大的搜索空间往往直接提供一个定义好空间,也不说明为什么采样这样的搜索空间。不同的搜索空间的设计有很强的先验性,即在好的搜索空间随机搜索也能找到不错的模型。
- 搜索算法与搜索空间的耦合。不同的文章采用不同搜索空间,无法直接比较不同搜索算法的好坏;“搜索空间”和“搜索算法”2个变量都在改变,公平的方式是控制变量法:1)在相同的搜索空间上,使用不同的搜索算法,比较不同搜索算法的优劣;2)在不同的搜索空间上,都采用随机搜索算法,比较不同搜索空间的优劣
- 可解释性不足。搜索过程类似一个黑盒过程,我们无法知道搜索的前进方向,也就无法解释为什么找到的结构能够提高模型表现。
- 可迁移性 / 泛化能力不足。即我们只能通过观察最后搜索到的个体的结构,来猜测什么样的结构是好的结构,无法明确知道搜索到的某个结构是否是对当前任务的“过拟合”(只适用于当前任务),还是普适性的(可以推广到其他任务/不同平台上的)。
创新点
而本文的方法是 focus 在 “群体估计” 层面,即我们不是希望找到一个最好的模型个体,而是希望找到表现很好的 模型群体。通过逐步设计模型的“搜索空间”,希望逐渐提高搜索空间内“优质模型”的浓度。
针对以上几个问题,本文分别通过以下方式解决:
- 搜索空间先验性太强:不引入关于搜索空间空间设计的先验知识,从一个几乎没有约束的搜索空间出发,根据实验结果逐步缩小搜索空间。
- 搜索算法与搜索空间的耦合:本文focus在 搜索空间的设计,因此为了排除搜索算法的影响,不使用任何先进的搜索算法,对不同的搜索空间都使用随机搜索。即控制变量法:在不同的搜索空间上,都采用随机搜索,比较不同搜索空间的优劣。
- 可解释性不足:从一个几乎没有任何约束的搜索空间出发,通过严格的控制变量,每次实验只改变单一的变量,探究该变量对搜索空间质量(优质模型的浓度)的影响;这样我们可以清楚地看到每次模型空间的进化方向,为模型设计提供了一定的可解释性。
- 可迁移性 / 泛化能力不足:通过在最优的RegNet空间上进行不同flops,不同epochs,不同stage,不同block types的实验,证明RegNet的泛化能力。
方法
3 Design Space Design
模型的设计空间是一个巨大的,可能是无穷的模型群体空间。那么如何评价不同的模型空间呢,我们根据统计学的思想,通过在某个模型空间内抽样,得到模型性能分布,作为评估该空间好坏的标准。
在该部分中,我们从一个初始化的无限制的空间开始,逐步添加限制条件,设计简化后的搜索空间。
在我们设计过程的每个步骤中,输入是初始空间,输出是简化后的空间。每个步骤的目的是为了探究不同的设计原则能否得到更简单的,质量更好的模型空间。
3.1 Tools for Design Space Design
如何评价不同模型空间的好坏?我们提出了一种量化模型空间质量的方法:通过在空间内随机抽样出不同的模型,并通过这些模型的 性能分布(error distribution) 来刻画该空间的质量。这样做的动机是对比不同空间样本的性能分布,比对比不同空间内搜索到的最佳模型的性能,更鲁棒,前者更能代表一个空间的质量。
为了得到一个空间内模型的性能分布,我们在该空间中抽样并训练n个模型,为了提高效率,我们只抽样大小为400MF(即400M FLOPs)的模型样本,每个样本在ImageNet数据集上训练10个epochs。
作者这里假设,由于抽样大量的样本,每个样本训练10个epoch的后的群体性能足以刻画该空间的质量。
我们刻画模型空间性能的指标是EDF(Error Distribution Function):
\(F(e)\) 代表所有样本中,模型的错误率小于e的的比例。(类似累积分布函数)

图2(左) 为从AnyNetX空间中采样500个模型的EDF函数图形。
对于一个训练好(10个epochs)的模型群体,我们可以画出模型特征(深度,宽度)与模型错误率的散点图:
图2(中) 为AnyNetX空间中采样的500个模型 的深度d与模型错误率err的关系
图2(右) 为AnyNetX空间中采样的500个模型 的第4个stage的宽度(stage下一节会介绍) 与模型错误率err的关系。
由于模型的性能(err)受到很多属性(深度,宽度,操作类型)的影响,类似一个高维的函数\(err=F(depth, width, ops...)\),散点图只画出了某一个属性和err的关系,可以认为是这个高维函数在某一个属性上的投影,可以帮助我们发现一些模型设计的规律。
在这些散点图中,我们采用 empirical bootstrap 来评估最优模型的可能范围。
empirical bootstrap:是一种统计估计方法,不假设样本分布,直接通过样本的值估计真实分布的一些统计量。
Bootstrap 的基本思想是:如果 观测样本 是从母体中随机抽取的,那么它将包含母体的全部的信息,那么我们不妨就把这个观测样本视为 “总体”。可以简单地概括为:既然样本是抽出来的,那我何不从样本中再抽样。
Bootstrap 的基本步骤如下:
- Step 1: 采用有放回抽样方法从原始样本中抽取一定数量的子样本。
- Step 2: 根据抽出的样本计算想要的统计量。
- Step 3: 重复前两步 K 次,得到 K 个统计量的估计值。
- Step 4: 根据 K 个估计值获得统计量的分布,并计算置信区间。
例如,我们现在想要知道 \(err=F(depth)\) ,最佳的depth的范围,我们可以通过如下步骤完成 empirical bootstrap:
给定n对 \((x_i,e_i)\),其中 \(x_i\) 表示模型的一个属性如 depth,\(e_i\) 表示对应的模型误差。
- 从这n对中随机采样25%,得到一组sample
- 选择这一组sample中 \(e_i\) 最小的一对
- 重复1-2步骤 \(10^4\) 次,一共得到 \(10^4\) 个样本对
- 计算这\(10^4\)对样本属性x的95%置信区间,并以中位数给出了最优可能的值。
从图2-middle,图2-right中来看,大概意思是,统计结果表明,属性(如depth)在浅蓝色区域的模型表现比外面好,最佳值可能是在黑线附近。
总的来说:
- 作者从一个设计空间中采样并训练n个模型
- 计算并画出决策空间的EDFs来表征设计空间的质量
- 使用 empirical bootstrap 来估算该设计空间不同属性的最佳取值的区间
- 根据可视化结果来调整设计空间
3.2 The AnyNet Design Space
最初始的,几乎没有任何限制的搜索空间记为 AnyNet
AnyNet空间的基本结构:stem => body => head,如图3a。
其中stem为3×3卷积,stride=2,输出通道(宽度)\(w_0=32\) ;body包含主要的计算量;head为池化和全连接层,输出n个类别。
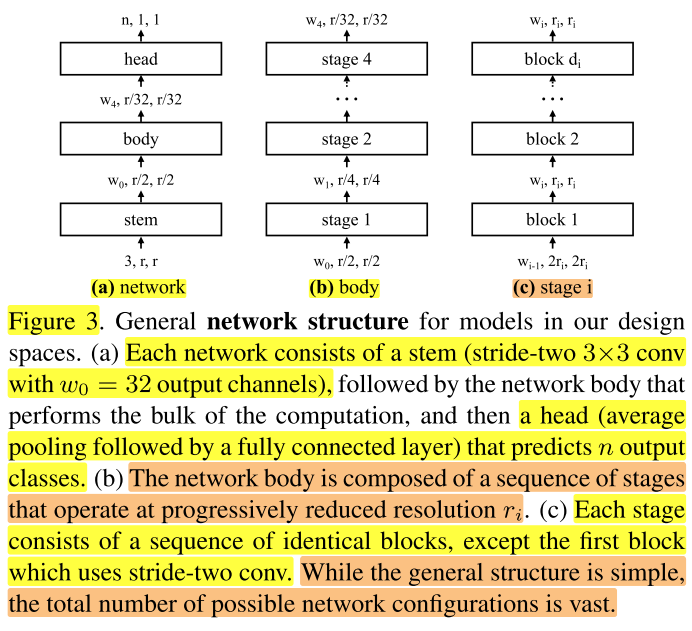
我们将stem和head固定,只探究body的结构变化的影响。
body:包含分辨率逐渐下降的4个stage(这里保持stage=4不变,后面会探究stage变化的影响)如图3b。
stage:第 \(i\) 个stage包含 \(d_i\) 个相同的block,每个block的宽度为 \(w_i\) 。
当前的设计空间称为 \(AnyNet\)
block:在大部分实验中,我们使用的block类型为:standard residual bottlenecks block with group convolution(如图4,左边stride=1,右边stride=2),记为 \(X\) block,(后面会探究block变化的影响)使用 \(X\) block的设计空间称为 \(AnyNetX\)

\(AnyNetX\) 空间大小分析:
每个模型包含4个stage,每个stage包含4个参数(block数 \(d_i\),block宽度 \(w_i\),bottleneck ratio \(b_i\), 和 group width \(g_i\)),我们将输入分辨率固定为 r=224(后面会讨论输入分辨率的影响),因此每个模型都由 \(4个stage×每个stage4个参数=16个参数\) 决定。
参数取值范围:(block数 \(d_i≤16\),block宽度 \(w_i≤1024\) 且可以被8整除,bottleneck ratio \(b_i∈\{1,2,4\}\), 和 group width \(g_i∈\{1,2,4,8,16,32\}\))
| 参数 | 取值 | 规模 |
|---|---|---|
| block 的 数量 \(d_i\) | \(\{1,2,3,...16\}\) | 16 |
| block 的 宽度 \(w_i\) | \(\{8,16,24,...1024\}\) | 128 |
| block 的 bottleneck ratio \(b_i\) | \(\{1,2,4\}\) | 3 |
| block 的 group width \(g_i\) | \(\{1,2,4,8,16,32\}\) | 6 |
| FLOPs | 400MF | 1 |
| epochs | 10 | 1 |
| stage数 | 4 | 1 |
| block类型 | X | 1 |
| 分辨率 r | 224 | 1 |
因此 \(AnyNetX\) 空间大小为:\((16×128×3×6)^4≈10^{18}\)
我们不是要搜索 \(AnyNetX\) 这个模型空间,而是借助上面提出的方法来探索更一般的设计原则,从而提供模型设计的可解释性和调整设计空间。在这个过程中我们的目标是:
- 简化设计空间
- 提高设计空间的可解释性
- 提高或者保持设计空间的质量
- 保持设计空间的多样性
\(AnyNetX\) 空间的基本统计信息如图2:

AnyNet\(X_A\)
为了进一步在 \(AnyNetX\) 上探究,我们将上面的 \(AnyNetX\) 空间(即原始的 \(AnyNetX\) 空间记为 \(AnyNetX_A\)
| 参数 | 取值 | 规模 | 空间 |
|---|---|---|---|
| 第i个stage block 的 bottleneck ratio \(b_i\) | \(\{1,2,4\}\) | 3 | |
| 第i个stage block 的 group width \(g_i\) | \(\{1,2,4,8,16,32\}\) | 6 | |
| 第i个stage block 的 宽度 \(w_i\) | \(\{8,16,24,...1024\}\) | 128 | |
| 第i个stage block 的 数量 \(d_i\) | \(\{1,2,3,...16\}\) | 16 | |
| FLOPs | 400MF | 1 | |
| epochs | 10 | 1 | |
| stage数 | 4 | 1 | |
| block类型 | X | 1 | |
| 分辨率 r | 224 | 1 |
AnyNet\(X_B\)
将 \(AnyNetX_A\) 设计空间中的所有的stage i 都采用同一个bottleneck ratio \(b_i\)=b,得到新的设计空间为 \(AnyNetX_B\) 。
| 参数 | 取值 | 规模 | 空间 |
|---|---|---|---|
| 第i个stage block 的 bottleneck ratio \(b_i\) | \(\{1,2,4\}=>\{b\}\) | 3 => 1 | AnyNet\(X_B\) |
| 第i个stage block 的 group width \(g_i\) | \(\{1,2,4,8,16,32\}\) | 6 | |
| 第i个stage block 的 宽度 \(w_i\) | \(\{8,16,24,...1024\}\) | 128 | |
| 第i个stage block 的 数量 \(d_i\) | \(\{1,2,3,...16\}\) | 16 | |
| FLOPs | 400MF | 1 | |
| epochs | 10 | 1 | |
| stage数 | 4 | 1 | |
| block类型 | X | 1 | |
| 分辨率 r | 224 | 1 |
\(AnyNetX_B\) 的统计信息如图5左。可以看到两者曲线基本保持一致,也就是说当所有的stage i 都采用同一个bottleneck ratio时,网络精度并没有损失。这样处理除了简化了设计空间之外, \(AnyNetX_B\) 更容易分析,如图5右所示,b的95%置信区间为b≤2。
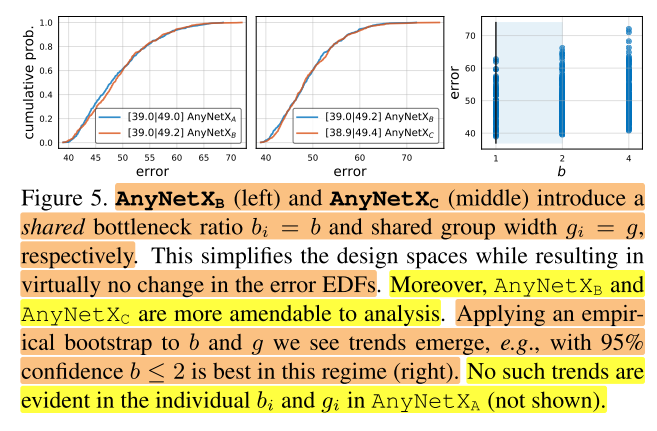
AnyNet\(X_C\)
在 \(AnyNetX_B\) 基础上,在进一步保持各个stage i都采用同一个group width \(g_i=g\),得到新的设计空间为 \(AnyNetX_C\) 。如图5中所示,当所有的stage i 都采用同一个group width时,网络精度并没有损失。这样就可以进一步简化设计空间, \(AnyNetX_C\) 比 \(AnyNetX_A\) 减少了6个自由度( \(AnyNetX_A\) 中4个stage,每个stage 都有 \(g_i\) 和 \(b_i\) ,共8个参数; \(AnyNetX_C\) 中只有2个参数,减少了6个参数)。另外,作者发现当g>1时是最优的(实验没有展示出来),这部分在第4节进行详细介绍。
| 参数 | 取值 | 规模 | 空间 |
|---|---|---|---|
| 第i个stage block 的 bottleneck ratio \(b_i\) | \(\{1,2,4\}=>\{b\}\) | 3 => 1 | AnyNet\(X_B\) |
| 第i个stage block 的 group width \(g_i\) | \(\{1,2,4,8,16,32\}=>\{g\}\) | 6 => 1 | AnyNet\(X_C\) |
| 第i个stage block 的 宽度 \(w_i\) | \(\{8,16,24,...1024\}\) | 128 | |
| 第i个stage block 的 数量 \(d_i\) | \(\{1,2,3,...16\}\) | 16 | |
| FLOPs | 400MF | 1 | |
| epochs | 10 | 1 | |
| stage数 | 4 | 1 | |
| block类型 | X | 1 | |
| 分辨率 r | 224 | 1 |
接着作者对 \(AnyNetX_C\) 中的最好的结构(图6上)和最差的结构(图6下)进行了分析。图中,横坐标是block id,而纵坐标是block的宽度\(w\)。例如下面第一幅图就表示,第一个stage有一个block,宽度为48;第二个stage有2个block,宽度为80;以此类推。

从图6中可以发现好的网络都有一个共同的属性,网络的宽度逐渐增加,也就是说\(w_{i+1}≥w_i\),我们添加该约束,
AnyNet\(X_D\)
添加约束\(w_{i+1}≥w_i\) ,有该约束的设计空间称为 \(AnyNetX_D\) 。画出该空间的EDF曲线,如图7(左)所示,发现通过该原则,能够极大的提高EDF。
| 参数 | 取值 | 规模 | 空间 |
|---|---|---|---|
| 第i个stage block 的 bottleneck ratio \(b_i\) | \(\{1,2,4\}=>\{b\}\) | 3 => 1 | AnyNet\(X_B\) |
| 第i个stage block 的 group width \(g_i\) | \(\{1,2,4,8,16,32\}=>\{g\}\) | 6 => 1 | AnyNet\(X_C\) |
| 第i个stage block 的 宽度 \(w_i\) | \(\{8,16,24,...1024\} + const(w_{i+1} ≥ w_i)\) | 128 => (≤128) | AnyNet\(X_D\) |
| 第i个stage block 的 数量 \(d_i\) | \(\{1,2,3,...16\}\) | 16 | |
| FLOPs | 400MF | 1 | |
| epochs | 10 | 1 | |
| stage数 | 4 | 1 | |
| block类型 | X | 1 | |
| 分辨率 r | 224 | 1 |

AnyNet\(X_E\)
通过观察更多的模型(没有画出来),作者发现对于比较好的模型,每一个stage的宽度 di 也有逐渐增加的趋势,但是最后一个stage并不需要。虽然如此,作者约束 \(d_{i+1}≥d_i\) 得到新的设计空间 \(AnyNetX_E\) ,然后画出该空间的EDF曲线,如图7(右)所示,发现通过该原则,也能提高EDF。
| 参数 | 取值 | 规模 | 空间 |
|---|---|---|---|
| 第i个stage block 的 bottleneck ratio \(b_i\) | \(\{1,2,4\}=>\{b\}\) | 3 => 1 | AnyNet\(X_B\) |
| 第i个stage block 的 group width \(g_i\) | \(\{1,2,4,8,16,32\}=>\{g\}\) | 6 => 1 | AnyNet\(X_C\) |
| 第i个stage block 的 宽度 \(w_i\) | \(\{8,16,24,...1024\} + const(w_{i+1} ≥ w_i)\) | 128 => (≤128) | AnyNet\(X_D\) |
| 第i个stage block 的 数量 \(d_i\) | \(\{1,2,3,...16\} + const(d_{i+1}≥d_i)\) | 16 => (≤16) | AnyNet\(X_E\) |
| FLOPs | 400MF | 1 | |
| epochs | 10 | 1 | |
| stage数 | 4 | 1 | |
| block类型 | X | 1 | |
| 分辨率 r | 224 | 1 |
靠着一步步的优化,缩小设计空间,作者最终得到了大量包含优质模型且设计空间较小的 \(AnyNetX_E\) 。
3.3 The RegNet Design Space
为了更好的理解模型结构,从 \(AnyNetX_E\) 中选出最好的20个模型,然后画出来每个block id 和 block 宽度 \(w_i\) 的关系,如图8左上所示。
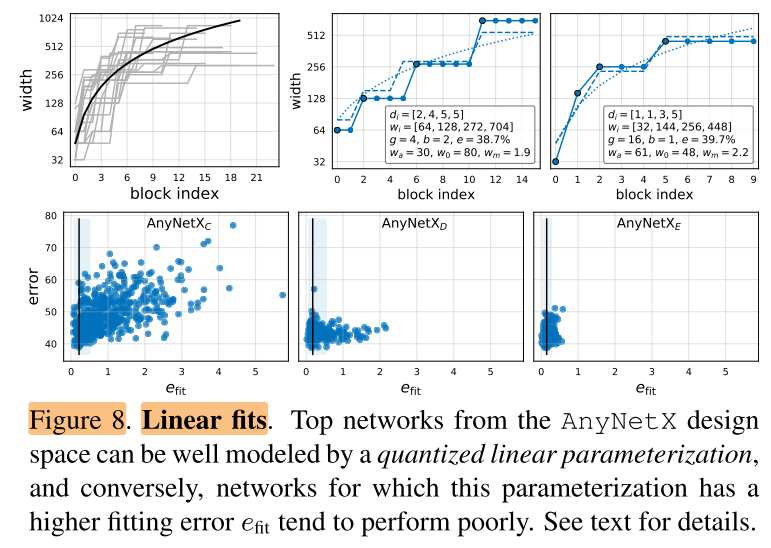
虽然每个模型之间的差异巨大,但是整体上表现出来了一种 block宽度 随着 block index 上升的趋势,即当 \(0≤j≤20\) 时,可以用简单的线性拟合: \(w_j=48⋅(j+1)\) ,也就是图8左上图中的黑线(由于纵坐标是取log后的,因此在图中为曲线)。但是这种量化方式,对于每一个block j都指定了一个特定的宽度 \(w_j\),但是实际上模型的 \(w_j\) 是量化的(由于每个stage的block的 \(w_j\) 都是相同的,因此4个stage时, \(w_j\) 只有4个取值),因此应该采用阶梯函数来拟合,而不是使用线性函数。
采用以下步骤:
- 先用拟合一个线性函数
- 量化这个线性函数,得到一个阶梯函数
简单地说就是算出来的宽度可能是126.123之类的奇葩数字,得给它四舍五入到128这种科学的数字,同时每个stage i有很多block,得把宽度统一到某个数字。这就需要拿一个阶梯函数去近似上面的线性函数。
量化线性函数的步骤:
线性函数: \(u_j=w_0+w_a \cdot j \quad for \quad 0≤j<d \qquad (2)\) ,j是blcok id,\(u_j\) 是第 j 个block 的宽度
引入一个参数 \(w_m>0\) ,等式(2)可以改写为 \(u_j=w_0 \cdot w_m^{s_j} \qquad (3)\) 的形式,其中 \(s_j\) 是根据(2)计算出来的,(2)(3)表达的是同一条直线
量化:将(3)中的 \(s_j\) 四舍五入,即可得到一个阶梯函数,实际量化中,限制 \(w_0>0, w_a >0\)
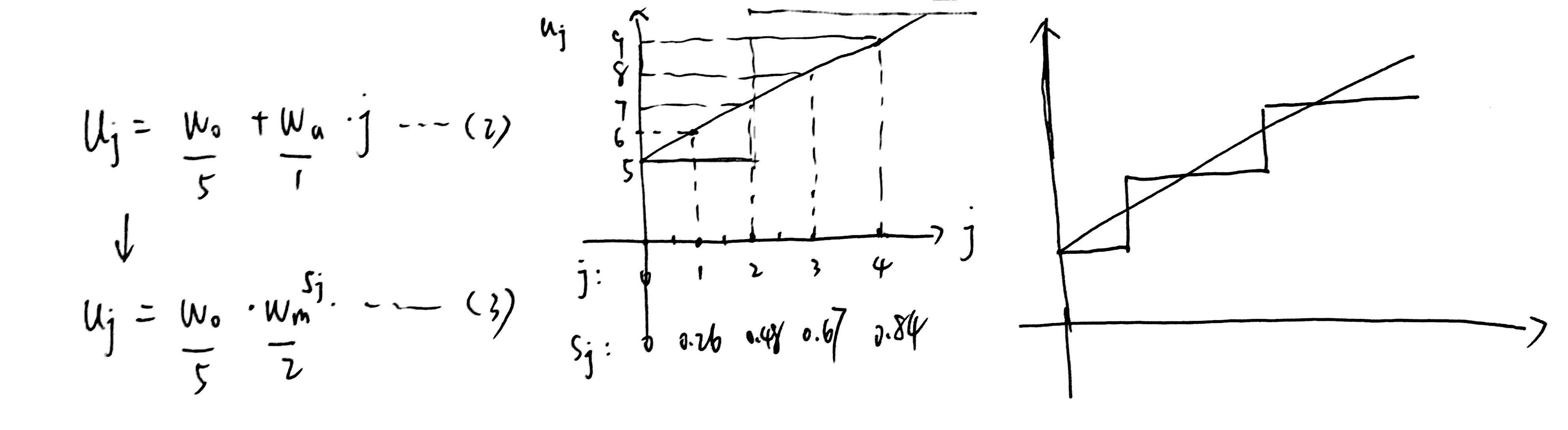
在\(AnyNetX\)空间验证,能否用这种方法拟合实际的模型样本。也就是说,给定一个模型空间,根据模型样本数据来拟合一个阶梯函数(即搜索一组超参,\(w_0,w_a,w_m\)),使得使用该拟合函数预测出的模型和实际给定的模型每一个block宽度之间的差异最小。该差异用 \(e_{fit}\) 表示。\(AnyNetX_D\) 和 \(AnyNetX_E\) 中的性能最好的2个模型如图8(上-中右)所示。可以看到量化后的函数(虚线)和这些模型(实线)拟合的很好,且 \(AnyNetX_E\) 中最佳模型的拟合效果最好。

接下来,我们画出拟合误差 \(e_{fit}\) 关于\(AnyNetX_C\)到 \(AnyNetX_E\) 中模型的曲线如图8(下)所示。
- 首先,观察到设计空间中最好的模型都有很好的拟合度。通过empirical bootstrap方法发现, \(e_{fit}\) 值接近零的一个窄带,可能包含每个设计空间中的最佳模型。
- 然后,可以发现从 \(AnyNetX_C\) 到 \(AnyNetX_E\) ,\(e_{fit}\) 越来越小(越来越容易拟合)。
为了进一步测试这种线性参数化的方法,基于 \(AnyNetX_E\) 限制 \(d<64,w_0,w_a<256\),\(1.5≤w_m≤3\),b和g与之前介绍的方式相同,在这个范围内采样,利用公式(2)-(4)得到具体的网络结构。
RegNetX
称有这种限制的空间为RegNetX( \(AnyNetX_E\) 加上3个拟合参数的限制)
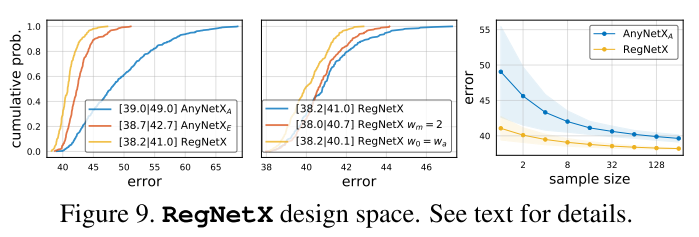
\(RegNetX\) 的EDF如图9(左)所示,可以看到RegNetX中的模型的平均误差比 \(AnyNetX_E\) 小,说明 \(RegNetX\) 中的模型都是比较优秀的模型。
从图9(中)作者进一步的对参数进行了限制,具体而言:
- 使用\(w_m\)=2(也就是stage之间的block宽度翻倍)轻微的提高了EDF,但是\(w_m\)≥2表现更好(后面展示)。
- 测试了 \(w_0\) = \(w_a\) ,进一步简化线性参数化方程为$ u_j= w_a ⋅(j+1)$。这样效果也变得更好了。
但是为了维持模型的重要性,作者并没有采样这两种限制。图9(右)展示了随机搜索的效率,发现RegNetX搜索大约随机采样32个模型就有可能产生好的模型。
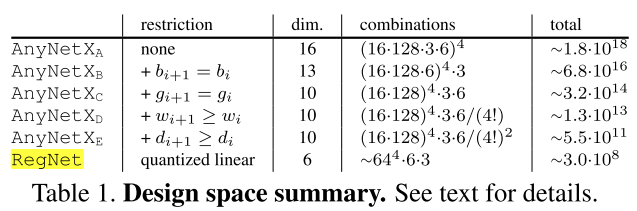
表1展示了决策空间尺寸的摘要。从原始的 \(AnyNetX\) 设计空间到 \(RegNet\) 设计空间,作者将自由维度从16缩小到了6,空间缩小了约10个数量级。然而 \(RegNet\) 仍然包含了设计空间的多样性。
3.4 Design Space Generalization
我们设计的 \(RegNet\) 设计空间是在low-compute, low-epoch的训练模式下进行的,只有一种block 类型。然而,我们的目标不是为单一设置设计一个设计空间,而是发现可以推广到新设置的网络设计的一般原则。
| 参数 | 取值 | 规模 | 空间 |
|---|---|---|---|
| 第i个stage block 的 bottleneck ratio \(b_i\) | \(\{1,2,4\}=>\{b\}\) | 3 => 1 | AnyNet\(X_B\) |
| 第i个stage block 的 group width \(g_i\) | \(\{1,2,4,8,16,32\}=>\{g\}\) | 6 => 1 | AnyNet\(X_C\) |
| 第i个stage block 的 宽度 \(w_i\) | \(\{8,16,24,...1024\} + const(w_{i+1} ≥ w_i)\) | 128 => (≤128) | AnyNet\(X_D\) |
| 第i个stage block 的 数量 \(d_i\) | \(\{1,2,3,...16\} + const(d_{i+1}≥d_i)\) | 16 => (≤16) | AnyNet\(X_E\) |
| FLOPs | 400MF => 800MF | / | |
| epochs | 10 => 50 | / | |
| stage数 | 4 => 5 | / | |
| block类型 | X | / | |
| 分辨率 r | 224 | / |
在图10,我们在higher flops, higher epochs, 5个stage, 不同种类的block类型(附录中详细说明)下比较了 \(AnyNetX_A\) 、 \(AnyNetX_E\) 和 \(RegNetX\) 设计空间。在各种模型空间下,都有\(RegNetX>AnyNetX_E>AnyNetX_A\)。换句话说,我们在特定限制下(400MF,10 epochs,4 stages)下发现的规则,在更大的搜索空间下同样有效,并不是特定限制的过拟合,说明这些规则具有一定的泛化能力。
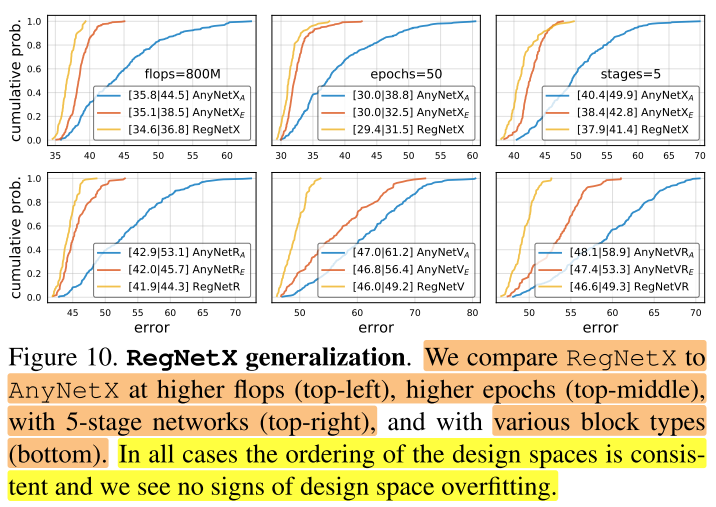
图10(下) 的不同blcok type(X、V、R、VR):
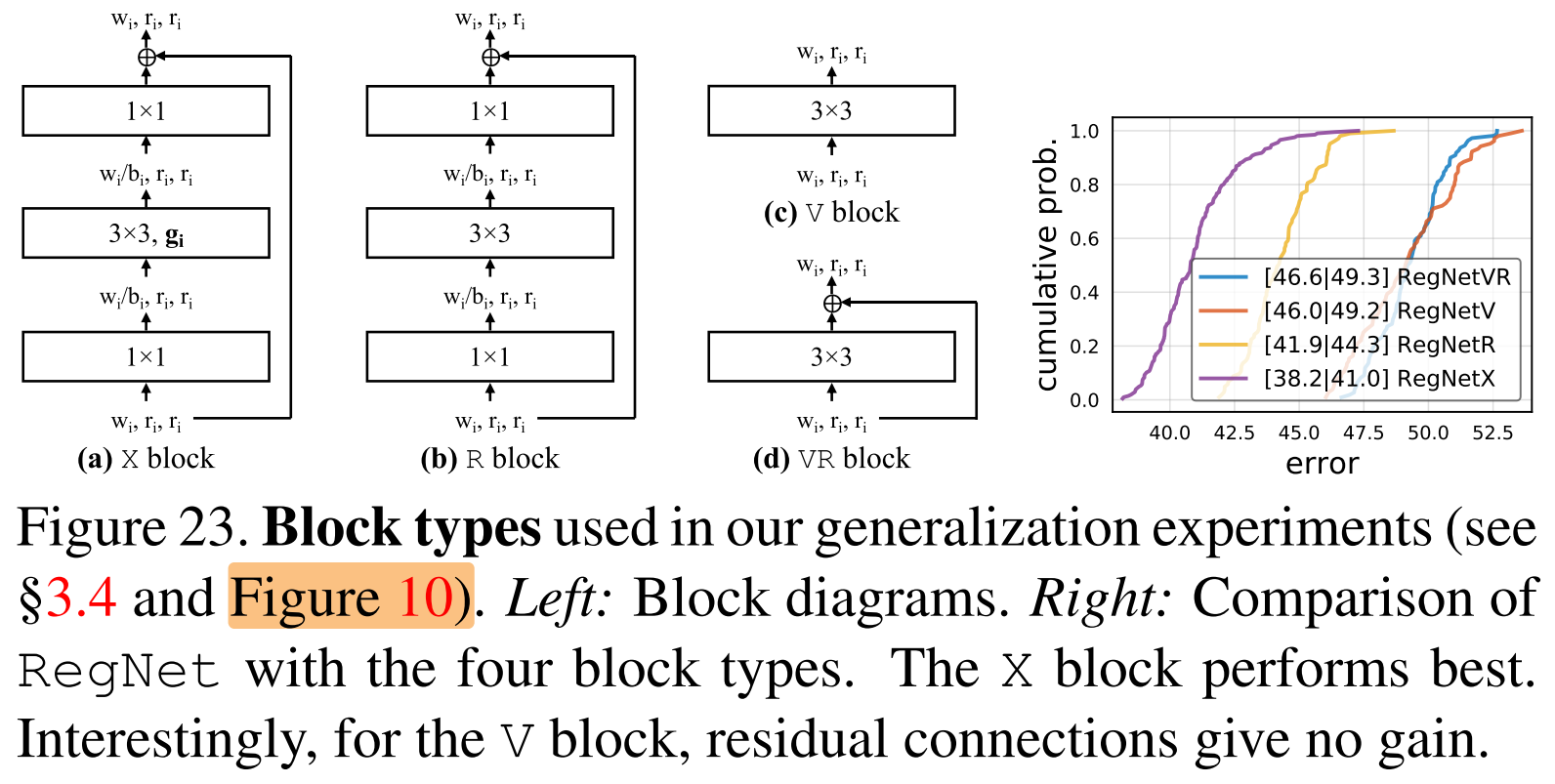
4. Analyzing the RegNetX Design Space
接下来进一步分析 \(RegNetX\) 设计空间,重新探讨深度网络设计的一些通用规则。 \(RegNetX\) 设计空间有大量的优秀模型,接下来的实验我们改为采样更少的模型(100)个,训练的epoch增多一点(25个)。这样就能观察到更加精细化的趋势。
RegNet trends.
图11中展示了RegNetX在不同FLOPs下各种参数的趋势。值得注意的是,通过图11(上左),发现在不同FLOPs下最优模型(黑色的线,使用empirical bootstrap得到)的depth都很稳定,大概为20个blocks(60层)。这与实际实践中,通常使用更深的模型以得到更高的性能的经验不同。通过图11(上中),发现最优模型的bottleneck ratio b=1.0。通过图11(上右),观察到最优模型的乘子\(w_m\)是2.5,这与实际经常采用的stage之间宽度翻倍的方式有点相似但是不完全相同。剩余的参数(g、 \(w_a\) 、 \(w_0\) )随着复杂度的增高而增加。

Complexity analysis.
除了FLOPs和参数,作者分析了所有卷积层的输出feature map的尺寸,将其定义为activations,用于度量网络的复杂度,在图12的左上角列出了常见卷积算子的复杂性度量。虽然activations不是衡量网络复杂性的通用标准,但activations可能会严重影响内存受限硬件加速器(例如GPU、TPU)上的运行时间,在图12(上)可以看到,activations与推理时间的正相关性比FLOPs更强。在图12(下)中,观察到对于总体中最好的模型,activations随FLOPs的平方根增加,参数量随FLOPs线性增加,并且推理时间最好使用FLOPs的线性和平方根项联合建模(即图12(下右)中的式子24f+6.0⋅f),因为它同时依赖于FLOPs和activations。
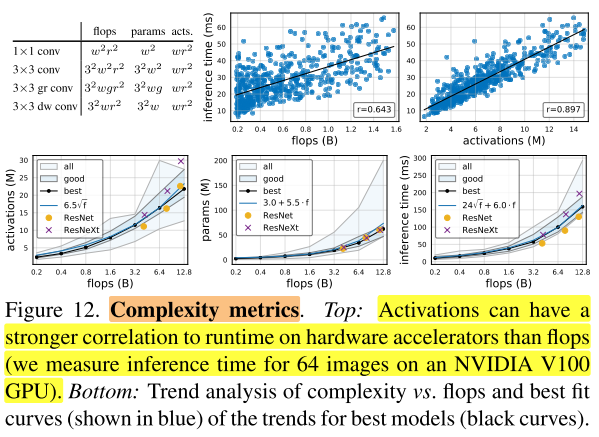
RegNetX constrained.
使用上述这些发现,我们可以对RegNetX设计空间进一步微调,首先基于图11(上),设置b=1,d≤40,\(w_m\)≥2 。然后基于图12(下),对参数量和activations进行约束。这样就能产生快速的、低参数量的、low-memory且不影响精度的模型。在图13中,我们对比了 \(RegNetX\) 有这些约束-C和没有这些约束-U下的表现,可以发现在所有FLOPs下,有约束的性能比没有约束的更好。因此在下面的实验结果小节都使用有约束的版本,然后更进一步的限制网络深度12≤d≤28(在附录D中有解释)。
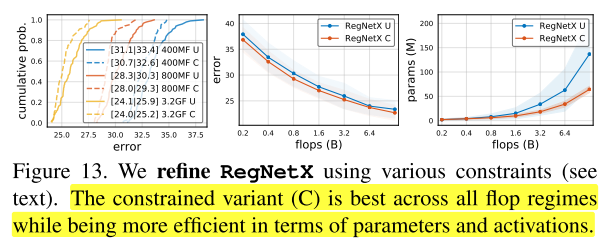
Alternate design choices.
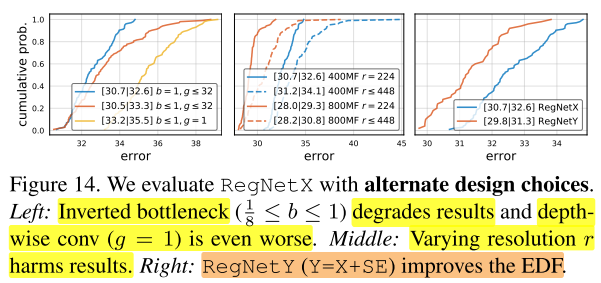
mobile network经常采用 inverted bottleneck (b < 1) 和depthwise conv。在图14(左),观察到相对于b=1,g≥1,inverted bottleneck (b<1) 轻微的降低了EDF,depthwise conv(group width \(g_i=1\) )表现更加差劲。
| 参数 | 取值 | 规模 | 空间 |
|---|---|---|---|
| 第i个stage block 的 bottleneck ratio \(b_i\) | \(\{1,2,4\}=>\{b\}\) | 3 => 1 | AnyNet\(X_B\) |
| 第i个stage block 的 group width \(g_i\) | \(\{1,2,4,8,16,32\}=>\{g\}\) | 6 => 1 | AnyNet\(X_C\) |
| 第i个stage block 的 宽度 \(w_i\) | \(\{8,16,24,...1024\} + const(w_{i+1} ≥ w_i)\) | 128 => (≤128) | AnyNet\(X_D\) |
| 第i个stage block 的 数量 \(d_i\) | \(\{1,2,3,...16\} + const(d_{i+1}≥d_i)\) | 16 => (≤16) | AnyNet\(X_E\) |
| FLOPs | 400MF => 800MF | / | |
| epochs | 10 => 50 | / | |
| stage数 | 4 => 5 | / | |
| block类型 | X | / | |
| 分辨率 r | 224 => | / |
接下来,作者测试了在不同输入图像分辨率对网络的影响,如图14(中)所示,与一般的结论相反,即使在更高的FLOPs,将RegNetX的分辨率固定为224×224表现更好。
SE.
最后,作者将block X和Squeeze-and-Excitation (SE)模块进行结合,得到了新的设计空间 \(RegNetY\) 。在图14(右),发现 \(RegNetY\) 性能提升比较明显。
Squeeze-and-Excitation Networks(SENet)是由自动驾驶公司Momenta在2017年公布的一种全新的图像识别结构,它通过对特征通道间的相关性进行建模,把重要的特征进行强化来提升准确率。这个结构是2017 ILSVR竞赛的冠军,top5的错误率达到了2.251%,比2016年的第一名还要低25%,可谓提升巨大。
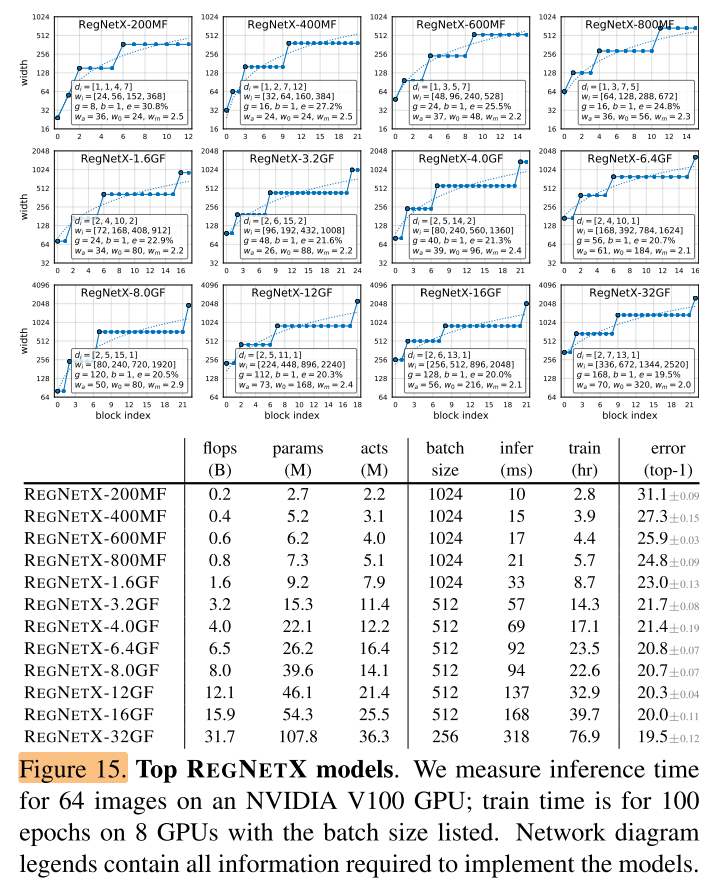
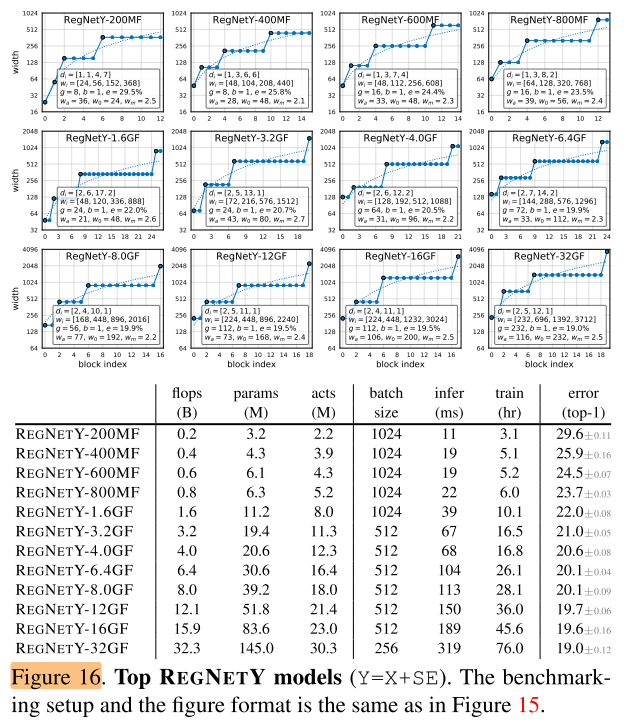
作者将 \(RegNetX\) 和 \(RegNetY\) 中的最优模型和目前State-of-the-art模型在各种FLOPs下进行对比。对于每一个FLOPs,作者从设计空间中选取最优模型,然后重新训练100个Epoch。在不同FLOPs下,RegNetX和RegNetY中的最优模型的参数与性能在图15和16中给出。
除了在上面第4章分析出的结论外,作者还发现了如下结论:
- 更高FLOPs的模型在stage 3中有更多的blocks,但是在stage4有更少的blocks,这和标准的ReNet网络设计相似。
- group width随着 g 的模型复杂度的提高而增加,但是 depth d 会饱和。
实验
5 Comparison to Existing Networks
5.1 State-of-the-Art Comparison: Mobile Regime
对于移动端,更加关注在600MF下模型的表现,作者比较了600MF \(RegNetX/Y\) 模型和现有的mobile网络。发现不管是人工设计的网络还是NAS搜索出的网络, \(RegNetX/Y\) 模型性能都更好。
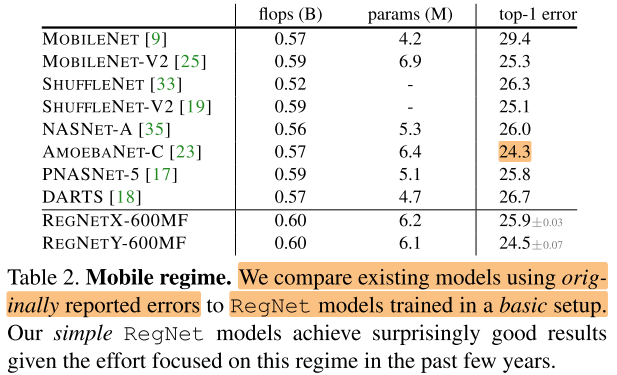
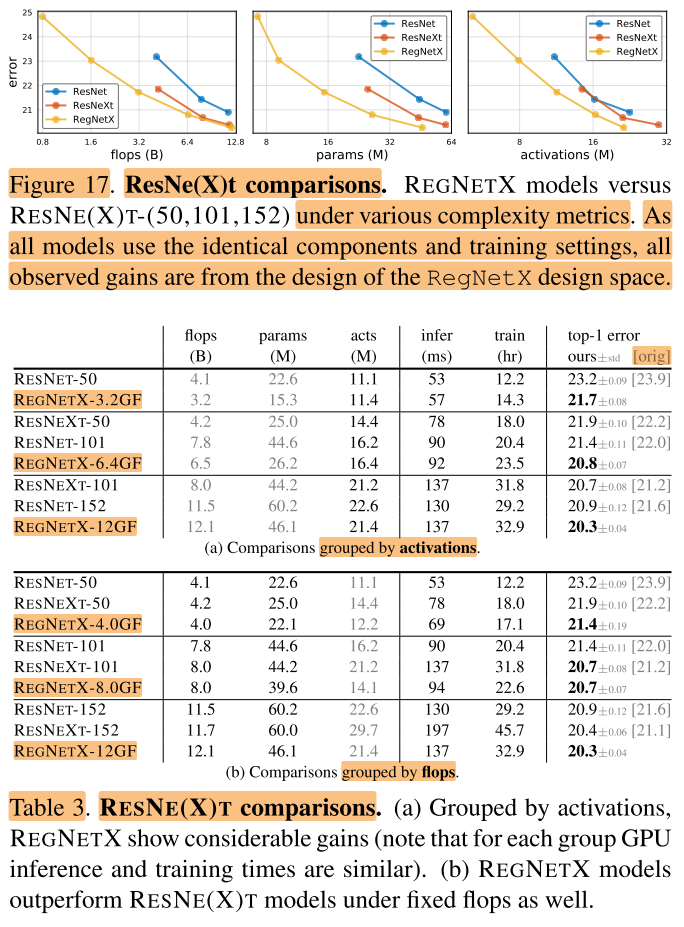
5.2 Standard Baselines Comparison: ResNe(X)t
作者将RegNet网络和标准的ResNet、ResNext网络进行对比。对比结果在图17和表3中给出。
可以发现只通过优化网络结构,RegNet可以取得巨大的提升。表3(a)在相近的activations下进行比较,表3(b)在相近的flops/params下进行比较,可以看出 \(RegNetX\) 模型性能都很好。
5.3 State-of-the-Art Comparison: Full Regime
作者将 \(EfficientNet\) 和 \(RegNetX\) 、\(RegNetY\) 进行比较,并控制两者在训练过程中参数一致,结果在图18和表4中给出。
从图18(左) 可以看出,在较低FLOPs下,EfficientNet表现比较好,但是在中等FLOPs下,RegNetY表现比EfficientNet好,在较高FLOPs下,RegNetX和RegNetY表现都比EfficientNet好。
还可以观察到,EfficientNet的activations随着FLOPs线性增长,而RegNet的activations随FLOPs的平方根增长。这导致了EfficientNet的GPU训练速度和推理速度较慢,例如RegNetX-8GF比EfficientNet的推理时间快了5倍,同时错误率更低。
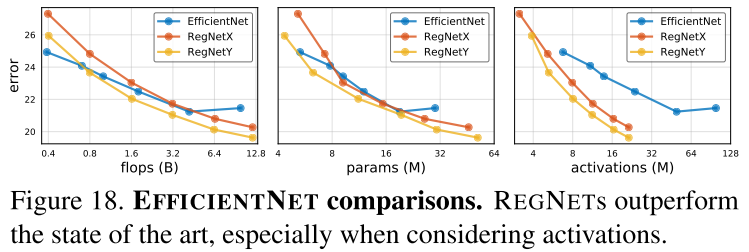
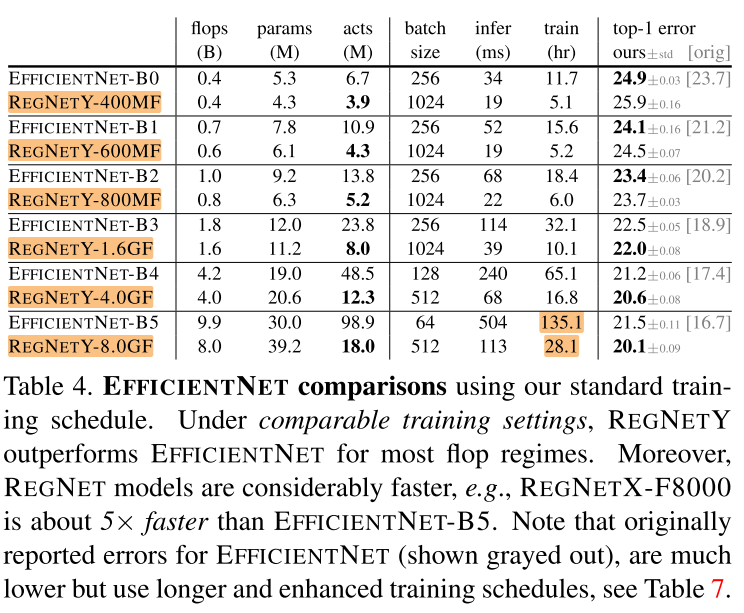
表4中的 orig

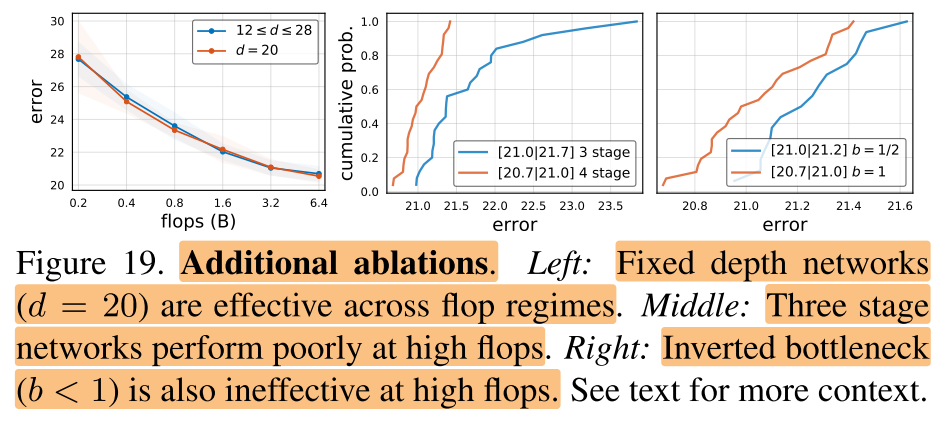
5.4 Additional Ablations
Fixed depth.
Fewer stages.
**Inverted Bottleneck. **
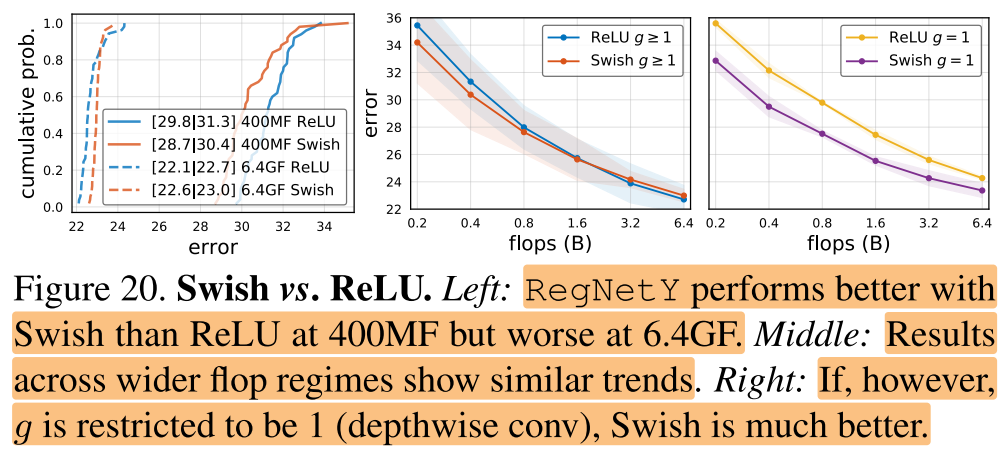
Swish vs. ReLU
最近的很多工作使用了swish激活函数,在图20中,作者对比了RegNetY在Swish and ReLU不同激励函数下的性能
图20(左中)可以看出swish激励函数在低FLOPs下表现更好,而ReLU激励函数在高FLOPs下表现更好。
图20(右)可以看出,如果g被约束到g=1(depthwise conv),那么swish函数比relu函数表现更好,也就是说swish函数和depthwise conv更加搭配。
总结
a、共享bottleneck ratio对效果无影响,\(AnyNet X_A => AnyNetX_B\)。
b、共享group width对效果无影响,\(AnyNetX_B=>AnyNetX_C\)。
c、逐步增大网络宽度能够提升效果,\(AnyNetX_C=>AnyNetX_D\)。
d、逐步增大网络深度能够提升效果,\(AnyNetX_D=>AnyNetX_E\)。
用线性函数来拟合block id与block宽度的关系
量化线性函数,添加量化参数约束,得到RegNet
| 参数 | 取值 | 规模 | 空间 |
|---|---|---|---|
| 第i个stage block 的 bottleneck ratio \(b_i\) | \(\{1,2,4\}=>\{b\}\) | 3 => 1 | =>AnyNet\(X_B\) |
| 第i个stage block 的 group width \(g_i\) | \(\{1,2,4,8,16,32\}=>\{g\}\) | 6 => 1 | =>AnyNet\(X_C\) |
| 第i个stage block 的 宽度 \(w_i\) | \(\{8,16,24,...1024\} + const(w_{i+1} ≥ w_i)\) | 128 => (≤128) | =>AnyNet\(X_D\) |
| 第i个stage block 的 数量 \(d_i\) | \(\{1,2,3,...16\} + const(d_{i+1}≥d_i)\) | 16 => (≤16) | =>AnyNet\(X_E\) |
| FLOPs | 400MF => 800MF | / | |
| epochs | 10 => 50 | / | |
| stage数 | 4 => 5 | / | |
| block类型 | X | / | |
| 分辨率 r | 224 => | / |
- 可解释性,步步递进,逐步细化子空间
- 泛化能力强,不人为引入先验知识,都是通过实验来发现规律
- 统计的方法
- 实验丰富


 浙公网安备 33010602011771号
浙公网安备 33010602011771号