2025XYCTF--Crypto--WriteUp

2025XYCTF--WriteUp

Complex_sigin

task：

from Crypto.Util.number import *
from Crypto.Cipher import ChaCha20
import hashlib
from secret import flag


class Complex:
    def __init__(self, re, im):
        self.re = re
        self.im = im

    def __mul__(self, c):
        re_ = self.re * c.re - self.im * c.im
        im_ = self.re * c.im + self.im * c.re
        return Complex(re_, im_)

    def __eq__(self, c):
        return self.re == c.re and self.im == c.im

    def __rshift__(self, m):
        return Complex(self.re >> m, self.im >> m)

    def __lshift__(self, m):
        return Complex(self.re << m, self.im << m)

    def __str__(self):
        if self.im == 0:
            return str(self.re)
        elif self.re == 0:
            if abs(self.im) == 1:
                return f"{'-' if self.im < 0 else ''}i"
            else:
                return f"{self.im}i"
        else:
            return f"{self.re} {'+' if self.im > 0 else '-'} {abs(self.im)}i"

    def tolist(self):
        return [self.re, self.im]


def complex_pow(c, exp, n):
    result = Complex(1, 0)
    while exp > 0:
        if exp & 1:
            result = result * c
            result.re = result.re % n
            result.im = result.im % n
        c = c * c
        c.re = c.re % n
        c.im = c.im % n
        exp >>= 1
    return result

bits = 128
p = getPrime(1024)
q = getPrime(1024)
n = p * q
m = Complex(getRandomRange(1, n), getRandomRange(1, n))
e = 3
c = complex_pow(m, e, n)
print(f"n = {n}")
print(f"mh = {(m >> bits << bits).tolist()}")
print(f"C = {c.tolist()}")
print(f"enc = {ChaCha20.new(key=hashlib.sha256(str(m.re + m.im).encode()).digest(), nonce=b'Pr3d1ctmyxjj').encrypt(flag)}")

'''
n = 24240993137357567658677097076762157882987659874601064738608971893024559525024581362454897599976003248892339463673241756118600994494150721789525924054960470762499808771760690211841936903839232109208099640507210141111314563007924046946402216384360405445595854947145800754365717704762310092558089455516189533635318084532202438477871458797287721022389909953190113597425964395222426700352859740293834121123138183367554858896124509695602915312917886769066254219381427385100688110915129283949340133524365403188753735534290512113201932620106585043122707355381551006014647469884010069878477179147719913280272028376706421104753
mh = [3960604425233637243960750976884707892473356737965752732899783806146911898367312949419828751012380013933993271701949681295313483782313836179989146607655230162315784541236731368582965456428944524621026385297377746108440938677401125816586119588080150103855075450874206012903009942468340296995700270449643148025957527925452034647677446705198250167222150181312718642480834399766134519333316989347221448685711220842032010517045985044813674426104295710015607450682205211098779229647334749706043180512861889295899050427257721209370423421046811102682648967375219936664246584194224745761842962418864084904820764122207293014016, 15053801146135239412812153100772352976861411085516247673065559201085791622602365389885455357620354025972053252939439247746724492130435830816513505615952791448705492885525709421224584364037704802923497222819113629874137050874966691886390837364018702981146413066712287361010611405028353728676772998972695270707666289161746024725705731676511793934556785324668045957177856807914741189938780850108643929261692799397326838812262009873072175627051209104209229233754715491428364039564130435227582042666464866336424773552304555244949976525797616679252470574006820212465924134763386213550360175810288209936288398862565142167552]
C = [5300743174999795329371527870190100703154639960450575575101738225528814331152637733729613419201898994386548816504858409726318742419169717222702404409496156167283354163362729304279553214510160589336672463972767842604886866159600567533436626931810981418193227593758688610512556391129176234307448758534506432755113432411099690991453452199653214054901093242337700880661006486138424743085527911347931571730473582051987520447237586885119205422668971876488684708196255266536680083835972668749902212285032756286424244284136941767752754078598830317271949981378674176685159516777247305970365843616105513456452993199192823148760, 21112179095014976702043514329117175747825140730885731533311755299178008997398851800028751416090265195760178867626233456642594578588007570838933135396672730765007160135908314028300141127837769297682479678972455077606519053977383739500664851033908924293990399261838079993207621314584108891814038236135637105408310569002463379136544773406496600396931819980400197333039720344346032547489037834427091233045574086625061748398991041014394602237400713218611015436866842699640680804906008370869021545517947588322083793581852529192500912579560094015867120212711242523672548392160514345774299568940390940653232489808850407256752]
enc = b'\x9c\xc4n\x8dF\xd9\x9e\xf4\x05\x82!\xde\xfe\x012$\xd0\x8c\xaf\xfb\rEb(\x04)\xa1\xa6\xbaI2J\xd2\xb2\x898\x11\xe6x\xa9\x19\x00pn\xf6rs- \xd2\xd1\xbe\xc7\xf51.\xd4\xd2 \xe7\xc6\xca\xe5\x19\xbe'
'''

analysis：

求解flag的前提条件就是求解m.re；m.im。

赛前看了一下往年的XYCTF的WP，2024年好像就有两道有关复数的RSA题型，拿到题后参考去年的复数思路去求解的。后面发现e是3，这个时候a,b的表达式是可以直接手算出来的：

\[设a = m.re,b = m.im;则c[0] \equiv a^3 - 3 ab^2(mod n);c[1]\equiv 3a^2b-b^3(modn).\\ 同时，我们有mh[0]=a_{high},mh[1]=b_{high}，两者皆缺少低128位，这个时候就可以利用二元Coppersmith攻击。 \]

exp：

# sage
import itertools

def small_roots(f, bounds, m=1, d=None):
    if not d:
        d = f.degree()

    R = f.base_ring()
    N = R.cardinality()

    f /= f.coefficients().pop(0)
    f = f.change_ring(ZZ)

    G = Sequence([], f.parent())
    for i in range(m + 1):
        base = N ^ (m - i) * f ^ i
        for shifts in itertools.product(range(d), repeat=f.nvariables()):
            g = base * prod(map(power, f.variables(), shifts))
            G.append(g)

    B, monomials = G.coefficient_matrix()
    monomials = vector(monomials)

    factors = [monomial(*bounds) for monomial in monomials]
    for i, factor in enumerate(factors):
        B.rescale_col(i, factor)

    B = B.dense_matrix().LLL()

    B = B.change_ring(QQ)
    for i, factor in enumerate(factors):
        B.rescale_col(i, 1 / factor)

    H = Sequence([], f.parent().change_ring(QQ))
    for h in filter(None, B * monomials):
        H.append(h)
        I = H.ideal()
        if I.dimension() == -1:
            H.pop()
        elif I.dimension() == 0:
            roots = []
            for root in I.variety(ring=ZZ):
                root = tuple(R(root[var]) for var in f.variables())
                roots.append(root)
            return roots

    return []

a_high = 3960604425233637243960750976884707892473356737965752732899783806146911898367312949419828751012380013933993271701949681295313483782313836179989146607655230162315784541236731368582965456428944524621026385297377746108440938677401125816586119588080150103855075450874206012903009942468340296995700270449643148025957527925452034647677446705198250167222150181312718642480834399766134519333316989347221448685711220842032010517045985044813674426104295710015607450682205211098779229647334749706043180512861889295899050427257721209370423421046811102682648967375219936664246584194224745761842962418864084904820764122207293014016
b_high = 15053801146135239412812153100772352976861411085516247673065559201085791622602365389885455357620354025972053252939439247746724492130435830816513505615952791448705492885525709421224584364037704802923497222819113629874137050874966691886390837364018702981146413066712287361010611405028353728676772998972695270707666289161746024725705731676511793934556785324668045957177856807914741189938780850108643929261692799397326838812262009873072175627051209104209229233754715491428364039564130435227582042666464866336424773552304555244949976525797616679252470574006820212465924134763386213550360175810288209936288398862565142167552
n = 24240993137357567658677097076762157882987659874601064738608971893024559525024581362454897599976003248892339463673241756118600994494150721789525924054960470762499808771760690211841936903839232109208099640507210141111314563007924046946402216384360405445595854947145800754365717704762310092558089455516189533635318084532202438477871458797287721022389909953190113597425964395222426700352859740293834121123138183367554858896124509695602915312917886769066254219381427385100688110915129283949340133524365403188753735534290512113201932620106585043122707355381551006014647469884010069878477179147719913280272028376706421104753
hint1 = 5300743174999795329371527870190100703154639960450575575101738225528814331152637733729613419201898994386548816504858409726318742419169717222702404409496156167283354163362729304279553214510160589336672463972767842604886866159600567533436626931810981418193227593758688610512556391129176234307448758534506432755113432411099690991453452199653214054901093242337700880661006486138424743085527911347931571730473582051987520447237586885119205422668971876488684708196255266536680083835972668749902212285032756286424244284136941767752754078598830317271949981378674176685159516777247305970365843616105513456452993199192823148760
hint2 = 21112179095014976702043514329117175747825140730885731533311755299178008997398851800028751416090265195760178867626233456642594578588007570838933135396672730765007160135908314028300141127837769297682479678972455077606519053977383739500664851033908924293990399261838079993207621314584108891814038236135637105408310569002463379136544773406496600396931819980400197333039720344346032547489037834427091233045574086625061748398991041014394602237400713218611015436866842699640680804906008370869021545517947588322083793581852529192500912579560094015867120212711242523672548392160514345774299568940390940653232489808850407256752

P.<x,y>=PolynomialRing(Zmod(n))

f = (a_high+x)^3-3*(a_high+x)*(b_high+y)^2-hint1
a_low , b_low=small_roots(f, [2^128,2^128],3)[0]

print("a =",a_high+a_low)
print("b =",b_high+b_low)

# -*- coding: utf-8 -*-
# @Author  : chen_xing
# @Time    : 2025/4/4 上午11:32
# @File    : exp.py
# @Software: Visual Studio Code
import hashlib
from Crypto.Cipher import ChaCha20


a = 3960604425233637243960750976884707892473356737965752732899783806146911898367312949419828751012380013933993271701949681295313483782313836179989146607655230162315784541236731368582965456428944524621026385297377746108440938677401125816586119588080150103855075450874206012903009942468340296995700270449643148025957527925452034647677446705198250167222150181312718642480834399766134519333316989347221448685711220842032010517045985044813674426104295710015607450682205211098779229647334749706043180512861889295899050427257721209370423421046811102682648967375219936664246584194224745762043102992820636089665887925419408029649
b = 15053801146135239412812153100772352976861411085516247673065559201085791622602365389885455357620354025972053252939439247746724492130435830816513505615952791448705492885525709421224584364037704802923497222819113629874137050874966691886390837364018702981146413066712287361010611405028353728676772998972695270707666289161746024725705731676511793934556785324668045957177856807914741189938780850108643929261692799397326838812262009873072175627051209104209229233754715491428364039564130435227582042666464866336424773552304555244949976525797616679252470574006820212465924134763386213550422285594849620684268131197026134044985

enc = b'\x9c\xc4n\x8dF\xd9\x9e\xf4\x05\x82!\xde\xfe\x012$\xd0\x8c\xaf\xfb\rEb(\x04)\xa1\xa6\xbaI2J\xd2\xb2\x898\x11\xe6x\xa9\x19\x00pn\xf6rs- \xd2\xd1\xbe\xc7\xf51.\xd4\xd2 \xe7\xc6\xca\xe5\x19\xbe'

key = hashlib.sha256(str(a + b).encode()).digest()
nonce = b'Pr3d1ctmyxjj'

cipher = ChaCha20.new(key=key, nonce=nonce)
flag = cipher.decrypt(enc)

print(f"flag = {flag}")

运行结果：

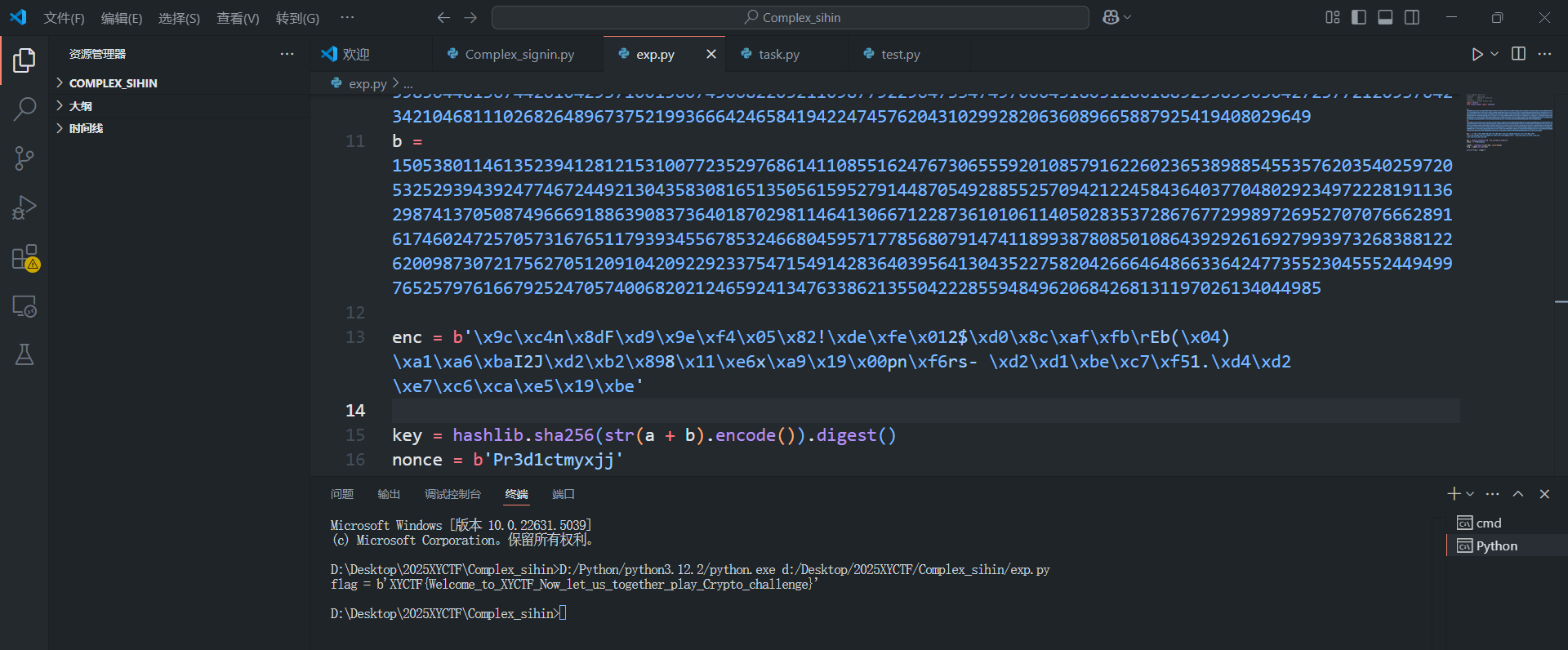
Division

task：

import random 
print('----Welcome to my division calc----')
print('''
menu:
      [1]  Division calc
      [2]  Get flag
''')
while True:
    choose = input(': >>> ')
    if choose == '1':
        try:
            denominator = int(input('input the denominator: >>> '))
        except:
            print('INPUT NUMBERS')
            continue
        nominator = random.getrandbits(32)
        if denominator == '0':
            print('NO YOU DONT')
            continue
        else:
            print(f'{nominator}//{denominator} = {nominator//denominator}')
    elif choose == '2':
        try:
            ans = input('input the answer: >>> ')
            rand1 = random.getrandbits(11000)
            rand2 = random.getrandbits(10000)
            correct_ans = rand1 // rand2
            if correct_ans == int(ans):
                with open('flag', 'r') as f:
                    print(f'Here is your flag: {f.read()}')
            else:
                print(f'The correct answer is {correct_ans}')
        except:
            print('INPUT NUMBERS')
    else:
        print('Invalid choice')

analysis：

随机数预测，翻阅资料或者deepseek。取前624次即可，我们可以每次都输入1，等号后就是我们需要的随机数分子。我们也可以随机输入分母，截取除号前面的部分，也是随机数分子。

local_test：

import random
from mt19937predictor import MT19937Predictor

# 模拟服务器生成随机数
random.seed(123)
nominators = [random.getrandbits(32) for _ in range(624)]

# 客户端预测
predictor = MT19937Predictor()
for n in nominators:
    predictor.setrandbits(n, 32)

# 生成rand1和rand2
rand1 = predictor.getrandbits(11000)
rand2 = predictor.getrandbits(10000)

# 真实值
true_rand1 = random.getrandbits(11000)
true_rand2 = random.getrandbits(10000)

assert rand1 == true_rand1 and rand2 == true_rand2  # 应通过

exp：

from pwn import *
from mt19937predictor import MT19937Predictor

conn = remote('47.93.96.189', 36972, timeout=15)
print("[+] 成功连接到服务器")

p = MT19937Predictor()
print("[+] 初始化 MT19937 预测器")

print("[*] 开始收集 624 个 32 位随机数...")
for i in range(624):
    conn.sendlineafter(b'>>> ', b'1')
    
    conn.sendlineafter(b'>>> ', b'1')
    
    response = conn.recvuntil(b'//')
    x = int(response[:-2].decode())
    
    p.setrandbits(x, 32)
    
    if (i+1) % 10 == 0 or (i+1) == 624:
        print(f"[+] 已收集 {i+1}/624 个随机数")

print("[+] 所有随机数收集完成！")

print("[*] 开始预测 rand1 (11000位) 和 rand2 (10000位)...")
rand1 = p.getrandbits(11000)
rand2 = p.getrandbits(10000)  
print(f"[+] rand1 位数: {len(bin(rand1))-2}")
print(f"[+] rand2 位数: {len(bin(rand2))-2}")

correct_ans = rand1 // rand2
print(f"[+] 计算答案: {correct_ans}")

print("[*] 提交答案...")
conn.sendlineafter(b'>>> ', b'2')
conn.sendlineafter(b'>>> ', str(correct_ans).encode())

print("[*] 接收服务器响应...")
flag = conn.recvall(timeout=10).decode()
print(flag)

conn.close()
"""
WOW
Here is your flag: XYCTF{9f9c47c3-1058-4bed-86a9-790f8c6d05e0}
"""

reed

task：

import string
import random
from secret import flag

assert flag.startswith('XYCTF{') and flag.endswith('}')
flag = flag.rstrip('}').lstrip('XYCTF{')

table = string.ascii_letters + string.digits
assert all(i in table for i in flag)
r = random.Random()

class PRNG:
    def __init__(self, seed):
        self.a = 1145140
        self.b = 19198100
        random.seed(seed)

    def next(self):
        x = random.randint(self.a, self.b)
        random.seed(x ** 2 + 1)
        return x
    
    def round(self, k):
        for _ in range(k):
            x = self.next()
        return x

def encrypt(msg, a, b):
    c = [(a * table.index(m) + b) % 19198111 for m in msg]
    return c

seed = int(input('give me seed: '))
prng = PRNG(seed)
a = prng.round(r.randrange(2**16))
b = prng.round(r.randrange(2**16))
enc = encrypt(flag, a, b)
print(enc)
"""
enc = [8795335, 8795335, 7727375, 972018, 8795335, 7727375, 6684584, 5616624, 276824, 13439941, 997187, 15923458, 3480704, 5616624, 10236061, 8100141, 5616624, 14855498, 14855498, 3480704, 997187, 2065147, 10236061, 19127338, 13439941, 2412744, 3480704, 1344784, 14855498, 8795335, 12346812, 8795335, 12346812, 19102169, 8795335, 15550692]
"""

analysis：

首先，针对于random中的函数分为显式赋值种子和隐式赋值种子，在本题中我们输入的种子会被全局隐式赋值，也就是说seed一样的前提下，本地与远程同一次运行语句x = random.randint(self.a, self.b)会生成一样的结果。但是由于我们并不能显式地为实例化对象r进行种子赋值，所以这就导致a = prng.round(r.randrange(2**16))无法预测，这从r = random.Random()这条语句运行后就已经决定了，因为它采用的是os.urandom()作为种子，其为纳秒级别，经测试，prng.round()产生的不同的随机数会在2**13时达到上限6197个。如果我们想直接爆破a,b，我们最多大概需要爆破6197*6197=38,402,809次。但是这里由于encrypt中存在漏洞(下称该6197个数字为b_probability)：

c = a * table.index(m) + b) % 19198111，而table.index(m)当m="a"时为0，同时我们知道，a,b取自这6197个数字中的两个。也就是说，如果flag中存在"a"那么就有b = c。我们通过遍历enc，如果enc与b_probability相同元素，那么该值为b。接着去求解a：

我采用的思路是首先我们把enc去重，设为enc_set，随机选两个进行作差，由于len(table) = 64，这个时候我取(a * i + b) % m ≡ enc_set[0]和(a * j + b) % m ≡ enc_set[1]，故a * (i - j) % m ≡ enc_set[0] - enc_set[1]。而-64 ≤ i - j ≤ 64。求解同余方程获得a_probability。接着遍历a_probability和table，最多为128 * 64 = 8192次。当遇到c = enc_set[i]的时候进行计数，根据数据量的范围，只有正确的a和b才能保证计数器最后的数字与enc_set长度相等 ，否则大概率只能满足使用的两个同余式。a解出之后爆破table中的字符逐一匹配enc中的值即可。

test.py：

import string
import random
from Crypto.Util.number import inverse

b_probability = []

class PRNG:
    def __init__(self, seed):
        self.a = 1145140
        self.b = 19198100
        random.seed(seed)

    def next(self):
        x = random.randint(self.a, self.b)
        random.seed(x ** 2 + 1)
        b_probability.append(x)
        return x
    
    def round(self, k):
        for _ in range(k):
            x = self.next()
        return x

r = random.Random()

prng = PRNG(0)
# prng.round(2 ** 11)
# prng.round(2 ** 12)
prng.round(2 ** 13)
# prng.round(2 ** 16)
print(len(set(b_probability))) # 6197

exp：

import string
import random
from Crypto.Util.number import inverse

class PRNG:
    def __init__(self, seed):
        self.a = 1145140
        self.b = 19198100
        random.seed(seed)

    def next(self):
        x = random.randint(self.a, self.b)
        random.seed(x ** 2 + 1)
        b_probability.append(x)
        return x
    
    def round(self, k):
        for _ in range(k):
            x = self.next()
        return x

m = 19198111

r = random.Random()

table = string.ascii_letters + string.digits

enc = [8795335, 8795335, 7727375, 972018, 8795335, 7727375, 6684584, 5616624, 276824, 13439941, 997187, 15923458, 3480704, 5616624, 10236061, 8100141, 5616624, 14855498, 14855498, 3480704, 997187, 2065147, 10236061, 19127338, 13439941, 2412744, 3480704, 1344784, 14855498, 8795335, 12346812, 8795335, 12346812, 19102169, 8795335, 15550692]

b_probability = []

prng = PRNG(0)


prng.round(2 ** 13)

b_probability = list(set(b_probability))

for c in enc:
    if c in b_probability:
        b = c
        print(f"b = {b}")

a_probability = []
enc_set = list(set(enc))

for i in range(len(table)):
    try:
        inv = inverse(i, m)
        a_probability.append((enc_set[0] - enc_set[1]) * inv % m)
        a_probability.append((enc_set[1] - enc_set[0]) * inv % m)
    except ValueError:
        continue

for a_test in a_probability:
    temp = 0
    for i in range(len(table)):
        if (a_test * i + b) % m in enc_set:
            temp += 1
            if temp == len(enc_set):
                a = a_test
                print("a =", a)
                break

flag = []
for c in enc:
    for char in table:
        if (a * table.index(char) + b) % 19198111 == c:
            flag.append(char)
            break
print("XYCTF{" + "".join(flag) + "}")
"""
b = 2065147
a = 12442754
XYCTF{114514fixedpointissodangerous1919810}
"""