Codeforces Round 1022 (Div. 2) 题解及证明
Codeforces Round 1022 (Div. 2) 题解及证明
主播很菜,四题退场,还不会 e
现在只有 ABCD 题解
声明:所有区间左闭右开,数组编号 \([0, N)\)
A. Permutation Warm-Up
难度(个人感觉):\(\star\star\)(放在 a 题思维难度偏大)
看起来非常困难。
拆解一下,
\(\sum_{i=1}^N |a[i] - i|\),
一定有 N 个数取正号,N 个数取负号。
哪些值可取呢?
结论:一定是偶数,而所有不超过最大值(马上会给出)的偶数都可取
-
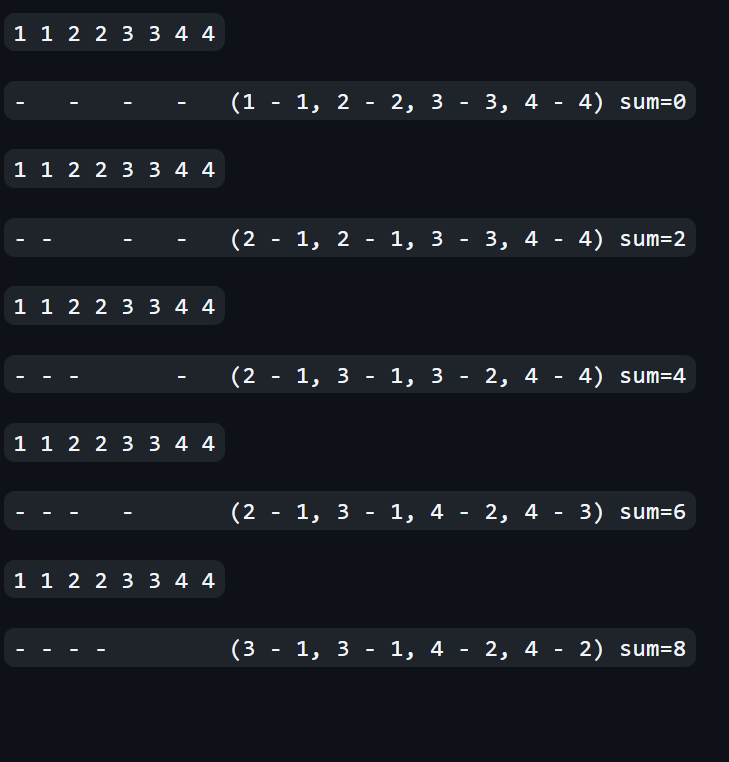
先决定数的符号,每种数有两个,先分别把一个取负号,此时为和为 0。不断将某个负号移到小 1 的数会导致和 sum += 2,每次可以通过 括号序列的方式 匹配,最终和会变为最大值。
以 N = 4 为例
![]()
-
还要还原到原数组上,我们将匹配的数连边,每个数度数为 2,所以我们的方案会形成一些环,然后把每个环变成有向的,构造 a 使得如果 u -> v,那么让 \(a[u] = v\)。
总之,0 到 最大值之间的偶数都是可取的,其中最大值即 2N 个数中,最小的 N 个取负号,即 \(max = \sum_{i=1}^N |(N + 1 - i) - i|\),答案是 \(max / 2 + 1\)。
B. SUMdamental Decomposition
难度(个人感觉):\(\star\star\)(需要分类讨论)
分类讨论 WA 了一发
总体思路是先把每个二进制位分给每个数,如果数多了就给他们分配 1 来抵消
记 p 为 popcount(x), p[i] 为 popcount(a[i]$);
-
若 \(n \le p\) 答案就是 \(x\)。这当然最优。
-
否则如果 \(n - p\) 是偶数,答案就是 \(x + n - p\),因为 \(\sum_{i=0}^{N-1} p[i] \ge x + n - p\)(前者给出 p 个,后者给出 N - p 个),
-
否则如果 \(n - p\) 是奇数,
-
2.1 如果 \(x \ge 2\),
那么先从小到大从前往后放 \(x\) 的二进制位,然后从后往前加入 1 即可。
比如 \(n = 6, x = 13\)
从小往大从前往后加入二进制位:
1 4 8
从后往前加入 1
1 4 (8+1) 1 1 1
答案是 \(x + ceil((n - p) / 2) * 2\)。这是最优的,因为 \(\sum_{i=0}^{N-1} p[i] \ge x + ceil((n - p) / 2) * 2\)(因为要求后者异或和为 0),
-
2.2 如果 \(x = 1\)
此时 \(p = 1, n\) 是偶数。我们需要让两个东西当一个1,其中最优的是 \(2 \oplus 3 = 1\)。 所以答案是 \((n - 2) + 2 + 3\)。这样做最优的原因是
不可能只多 1
(\(1 \oplus 1 \oplus ... \oplus 1 \oplus 2\) = 3)
或者多 2。
(\(1 \oplus 1 \oplus ... \oplus 1 \oplus 2\oplus 2\) = 3)
(\(1 \oplus 1 \oplus ... \oplus 1 \oplus 3\) = 3)
-
2.3 \(x = 0\)
此时 \(p = 0, n\) 是奇数。n > 1 时答案是 \((n - 2) + 2 + 3\)。
不可能只多 1
(\(1 \oplus 1 \oplus ... \oplus 1 \oplus 2\) = 2)
或者多 2。
(\(1 \oplus 1 \oplus ... \oplus 1 \oplus 2\oplus 2\) = 1)
(\(1 \oplus 1 \oplus ... \oplus 1 \oplus 3\) = 3)
特别的,\(n = 1\) 时无解。因为我们的替换方案至少要两个数。
-
C. Neo's Escape
难度(个人感觉):\(\star\star\)(思维难度适中)
结论:一种划分可行 当且仅当 每个 clone 能的管理一个 升-降(即先增后减) 的区间(这里升/降 的次数可以为 0),如 1 1 1,1 2 4,1 4 5 3 2。
证明:
\(\Leftarrow\), 即 升-将 划分都可行:将数组划分成先一些 升-降 区间,clone 按在其管理的区间的最大值处。每次找到数组中未访问最大的点,让管理它的 clone 移过去。如果这个点就是区间最大值,那么肯定没问题。否者由于上一个点更大,移动过程中一定不会访问更小点(否则存在 严格降-升 区间,但 升-降 区间中不存在这样的子区间),矛盾
\(\Rightarrow\),即 可行划分都是 升-将 划分:由于先访问大的再访问小的,相对起点同侧(即分别讨论起点左边的,起点右边的),靠近起点的一定先访问所以必须更大,也就是两侧都是相对起点(不严格)递降,即整个管理区域 升-降 区间
具体写法有两种,一种是直接遍历,\(d = 0\) 表示处于 升,\(d = 1\) 表示处于降
void solve(){
ans = 1;
bool d = 0;
for(int i = 1; i < N; i++){
if(d == 0 && !(a[i - 1] <= a[i])){
d = 1;
} else if(d == 1 && !(a[i - 1] >= a[i])){
ans++;
d = 0;
}
}
}
另一种写法是统计峰的个数
峰指先去重后,将第一个数之前,最后一个数之后安排极小值后, i 使得 \(a[i - 1] < a[i] < a[i + 1]\) 。容易说明每个峰管理一个区间,并且合起来就是整个区间。
void solve(){
ans = 0;
a.erase(std::unique(a.begin(), a.end()), a.end());
for(int i = 1; i + 1 < a.size(); i++){
ans += a[i - 1] < a[i] && a[i] > a[i + 1];
}
}
D. Needle in a Numstack
难度(个人感觉):\(\star\star\star\)(思维难度简单但范雷讨论很复杂)
思路是
-
分别找出 %k 的表 (=\(2k\) 次)
for(int i = 0; i < k; i++){ a[i % k] = query(i); } for(int i = N - k; i < N; i++){ b[i % k] = query(i); }如果 a 和 b 完全相同,那么 \(N = 2k\) 时分别是 \([0, k)\), \([k, N)\),否则不可判定。
不然就继续往下做
-
找到任意一个 a 和 b 中不同的 %k 的位,记作 diff。
-
二分出 a 中的 i 使得 \(i \% k == diff \; and \; C[i] == b[diff]\),记作 pos (\(\le ceil(log2(V=N/k)) \le 20\) 次)
-
往前走,找到第一个 i 使得 \(a[i] \% k != C[i] \; and \; b[i] \% k == C[i]\),记作 first 。(\(=k\) 次)
这个位置在 \((pos - k, pos]\) 之间,否则这个值后面第一个 \(\%k == diff\) 的位 i 比 pos 小但由于前面有个东西在 B 中,这个东西也一定在 B 中, \(C[i] == b[diff]\) 而 \(a[diff] != b[diff]\),与 pos 是最小的那个矛盾。
-
判断有没有可能相同(这个很复杂)
如果 \(first = k\), 前面一个数组一定只有 \(k\) 个数,即 \([0, k), [k, N)\)。
如果 \(first > N - k\), 后一个数组的开头一定在 \(N - k\) 及以前。如果第 \(N - k - 1\) 位有可能属于 a 也有可能属于 b,即 \(a[(N - k - 1) \% k] = b[(N - k - 1) \% k]\) 那么 \([0, N - k), [N - k, N)\) 和 \([0, N - k - 1), [N - k - 1, N)\) 都可行,输出 -1,否则分别是 \([0, N - k), [N - k, N)\)
否则 \(k < first <= N - k\),取 \([0, first), [first, N)\) 显然可行。如果第 \(first - 1\) 位有可能属于 a 也有可能是属于 b,即 \(a[(first) \% k] = b[(N - k - 1) \% k]\) 那么输出 -1,否则是唯一的。
总计 \(\le 170\) 次


 浙公网安备 33010602011771号
浙公网安备 33010602011771号