论文阅读笔记 连续学习中的EWC，DeepMind论文Overcoming catastrophic forgetting in neural networks
首先介绍下连续学习(Continuous Learning)吧。连续学习(Continuous Learning)又叫序列学习，顾名思义就是有顺序的学习任务。
参照人类，我们在遇到一个新的问题时，除非是完全陌生的领域，都会或多或少的利用之前所学的知识或技能来帮助自己更快的学习，而不是从零开始；而且在学习完新的知识或技能后，并不会完全忘记之前学过的东西。更直观的栗子：星星羽毛球打的贼溜，最近开始跟我们一起打篮球了，他学的就会比不怎么运动的东爷快，而且学完了并不会因此忘记了羽毛球怎么打。
人类是可以连续学习的。那么我们希望机器也有这个能力。
ProgressiveNN是这么解决这个问题的：
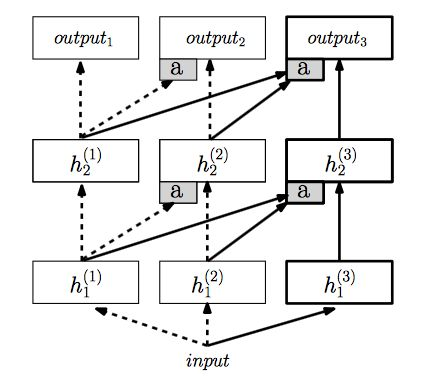
他们的方法简单暴力：对所有的之前任务的网络，保留并且fix，每次有一个新任务就新建一个网络（一列）。
而为了能使用过去的经验，他们同样也会将这个任务的输入输入进所有之前的网络，并且将之前网络的每一层的输出，与当前任务的网络每一层的输出一起输入下一层。
每次有一个新的任务，就重新添加一列，然后将前几列的输出fuse到当前列来。
比如说，如果两个任务的low level特征类似，则当前任务网络中的前几层可能完全没有用处，只需要用之前任务的输出就够了。
但是一个很明显的问题是，这个网络不能学到自己的low level feature的网络，然后使用之前网络的high level决策。因为1，当low level不一样的时候，将输入输入之前的网络就不make sense了；更重要的是，当前列的输入根本无法输入进之前列的网络，只复用高层网络根本无从谈起。
所以这里的限制就是，两个任务需要有类似的low level feature。
而Pathnet可以说是progressive nn的进阶版。
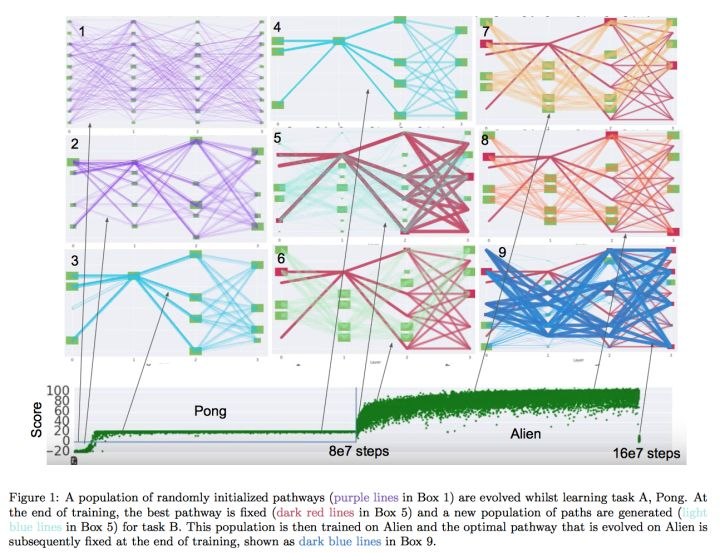
你可以把网络中每一层都看作一个模块（绿色方块），然后把构建一个网络看成搭积木。pathnet的想法就是复用积木。
一开始我们每一层都有N个候选模块，对每一个potential的网络，每一层可以使用k个模块。然后我们随机若干个网络（也就是path，如何连接这些模块），然后训练若干episodes。训练了之后，我们用遗传算法，把不好的path都淘汰，留下好的path，然后对这些path进行变异，然后继续训练。最后我们就能获得一个很好的path。（上图，从图1到图4）
注意，这个算法本身就是可以是一个独立的算法，用来训练一个任务。
而这个算法如何拓展到连续学习呢。在训练完第一个任务之后，我们将所有第一个任务path上的模块的参数都固定，然后将所有其他的模块重新初始化，然后像之前一样的训练。唯一的区别就是有些模块已经固定死了。（上图，图5到图9）
仔细一看，其实这跟progressive network非常类似，只是这里不再有列，而是不同的path。在pathnet的设定下，就不存在我之前所说无法访问高层的问题了。对一个新的任务，我们可以使用新的底层，然后用之前任务的高层。
EWC其实也是类似的想法。对之前任务学到的参数，我们应该进行保留；区别在于，ewc（elastic weight consolidation）用的是弹性的保留。
很重要的一点是，这里和pathnet和progressive nn不一样；EWC是使用一个网络来做不同的任务（而不是多个column或多个path）
我们看着这张图一步步来，首先最脑残的连续学习的方法就是，我们先训练了一个task1的网络，然后直接在task2上finetune（上图蓝色）。但是这样的问题就是，你学到了第二个任务之后，就就会基本忘记怎么做第一个任务了（这个就是catastrophic forgetting）。
然后你就想，那怎么办呢，那我就设个限制吧，在第二个任务上更新网络的时候，不能离第一个网络的参数太远，也就是相对于之前的网络参数上加了l2 regularizaiton。（上图绿色）
但是这样还不够好，然后就想到了。其实网络中有些参数是没有用的，有些参数是有用的，那我让那些重要的参数不要变太多，就更新哪些不重要的参数就行了嘛（上图红色）。然后这就是这篇文章的算法。你可以认为，就是对之前任务重要的参数，learning rate特别低，而那些不重要的，learning rate就相对高。而这个重要程度，则是使用fisher information。
他们做了analysis，用fisher information precision很好，但是有recall，因为他们只用了fisher information matrix的对角线，而没有考虑二元关系。
（上面这段摘自参考资料1的知乎专栏）
然后这个EWC，对应论文Overcoming catastrophic forgetting in neural networks就是我们今天的主角。思路大神罗若天已经讲过了（上面的摘抄），如果还不明白可以去看论文或者看参考资料2，我这里主要记录一下自己做的推导。因为论文里还是涉及了很多数学公式推导的，作为一个数学渣渣，我研究了好久…（是不是要被劝退了）。
论文中的公式1：
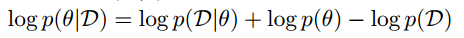
EWC的参照对象是SGD和加了相对previous task参数的L2正则。其核心思想是找到不同参数不同的重要性，对TaskA（Previous Task）重要的参数就更新幅度小一些，不重要的参数就可以多更新一些，这相对全部都加同样约束的L2正则就有了先进之处。这个重要程度则用Fisher Information来表示。费雪信息是啥呢？没关系我开始也不知道，后面需要用它的时候我会解释。
回到公式1。我们如果从概率的视角来看神经网络的训练，其实就是求条件概率$p(\theta\vert \mathcal{D})$。这个条件概率可以通过$p(\theta)$和$p(\mathcal{D}\vert\theta)$求（贝叶斯法则）。加对数就得到了公式1。
这里论文说，Note that the log probability of the data given the parameters $logp(\theta)$和$p(\mathcal{D}\vert\theta)$ is simply the negative of the loss function for the problem at hand $-L(\theta)$。
为啥呢？
首先，$logp(\theta)$和$p(\mathcal{D}\vert\theta)$这玩意儿似乎没有什么实际意义，所以不知道该咋求。所以我们需要找个东西去近似它，然后再求。那怎么近似呢？
我们看$logp(\theta)$和$p(\mathcal{D}\vert\theta)$的意义是啥。是给了$\theta$求数据集的分布。也就是说，如果$\theta$是对的，或者说在现有的$\theta$下，数据集分布越接近“正确”（现有$\theta$条件下的正确），概率就越大。或者反过来想，固定数据集，那么就是$\theta$越接近正确，这个概率就越大。（因为毕竟我们要求的是$\theta$，而条件概率$p(\mathcal{D}\vert\theta)$也可以被看做是$\theta$和D的多元函数）而$L(\theta)$的意义是这个$\theta$下的训练损失，$\theta$越接近这个数据集下正确的那个值，损失就越小，加个负号，就反过来想。
那么这两个东西的意义就是一致的了，于是就可以用这个损失去近似它。
然后论文提出了公式2，其中$D_A$,$D_B$是相互独立的，从数据集D中抽取出来的。
（相互独立意味着$p(A)p(B)=p(AB)$,$p(A\vert B)=p(A)$ 温习下相互独立和条件概率以及多个条件的条件概率？https://baike.baidu.com/item/%E6%9D%A1%E4%BB%B6%E6%A6%82%E7%8E%87)
于是有了公式2：
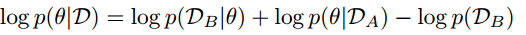
这个公式猛地有点懵逼，其实没有那么难，只是作者的记法有些晦涩，跳跃性太大了，如果这么写：
$\log p(\theta\vert \mathcal{D}_A, \mathcal{D}_B) = \log p(\mathcal{D}_B\vert \theta) + \log p(\theta\vert \mathcal{D}_A) - \log p(\mathcal{D}_B\vert \mathcal{D}_A)$
就相对容易明白一些了吧。D其实就是($D_A$,$D_B$)。
$p(\theta\vert D_A,D_B)=\frac{p(\theta,D_A,D_B)}{p(D_A,D_B)}=\frac{p(D_A)p(\theta\vert D_A)p(D_B\vert\theta,D_A)}{p(D_A)p(D_B\vert D_A)}=\frac{p(\theta\vert D_A)p(D_B\vert\theta)}{p(D_B)}$
其中最后一步$p(D_B\vert D_A)={p(D_B)$ $p(D_B\vert\theta,D_A)=p(D_B\vert\theta)$ 都是因为相互独立。
是不是就推出来啦。
公式2合理可用，那么咋用呢？
首先$logp(D_B\vert\theta)$可以用$-\mathcal{L}_B(\theta)$近似，前面说过了。
$logp(D_B)$直接归到常数里就好了。
$p(\theta\vert D_A)$咋办呢。它基本没法求，故要转换为等价的可计算的东西后再去近似计算。
论文用了Diagonalized Laplace Approximation得到了公式3：
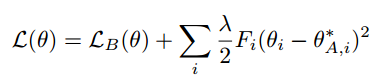
其中$F_i$是费舍尔信息矩阵的对角线元素。费舍尔信息矩阵是啥？Diagonalized Laplace Approximation是啥？
首先得学下（大神的话可以温习下）拉普拉斯近似方法。
给指个明路：
https://www.cnblogs.com/hapjin/p/8848480.html
https://blog.csdn.net/wangjian1204/article/details/49667611
https://blog.csdn.net/unixtch/article/details/77603738
如果期间对泰勒展开（多维），海森矩阵，正态分布（多维）产生了疑问：
https://baike.baidu.com/item/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83 正太分布
https://www.zhihu.com/question/25627482 泰勒展开式是啥？为啥能近似
https://zhuanlan.zhihu.com/p/33316479 多元泰勒展开式
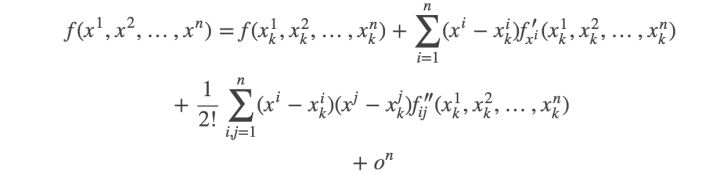
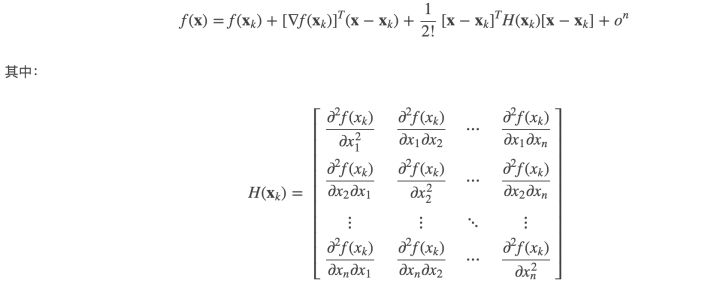
https://www.jianshu.com/p/7bf1d37751b3 梯度，雅各比矩阵，海森矩阵
https://www.cnblogs.com/emanlee/archive/2011/08/03/2126260.html 海森Hessian矩阵
费舍尔信息，费舍尔信息矩阵又是啥？
https://blog.csdn.net/lanran2/article/details/77995062 费舍尔信息为啥可以含有信息
https://www.zhihu.com/question/26561604 定义过程
是不是还没明白，看看wiki百科吧 https://en.wikipedia.org/wiki/Fisher_information
（费舍尔信息这块儿还有些推导需要整理一下）
首先，我们知道，信息量是用样本发生的概率来衡量的（$-logp_A$）。一个事件发生的概率越大，那么它的信息量就越小，说明我们可以在这条样本上学习到的东西就越少。相反如果一个事件发生的概率很小，那么我们可以认为该样本携带了很多信息。
对于随机变量$X～f(X|\theta)$,其似然函数为：
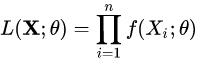
当参数$\theta$取到的值接近准确值时，似然函数的值应该很大，所以当参数w取到准确值时，似然函数的值应该取到最大值，或者（对数）似然函数的一阶导数为0。
那么，（为了方便，下面w和$\theta$混用了）其对数似然函数(省略求和符号）$log^{'}f(x|w) = \frac{{\partial{logf(x|w)}}}{\partial{w}} = \frac{{f(x|w)^{'}}}{f(x|w)}$
如果log′(x|w)非常接近于0，那么我们基本学习不到太多跟参数w有关的知识，换句话说模型基本不会更新了；相反，如果|log′(x|w)|很大，那么样本就提供了比较多的关于参数w的信息。因此，我们可以用|log′(x|w)|的平方来衡量提供的信息（information）。
这个log likelihood的一阶导数也叫，Score function ：
那么Fisher Information，用表示，的定义就是这个Score function的二阶矩（second moment）
。
其中，。因为
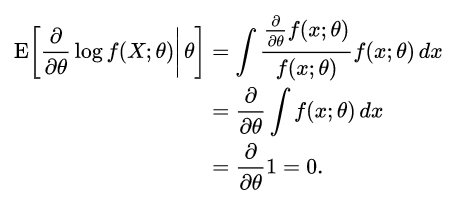
所以
If log f(x; θ) is twice differentiable with respect to θ, and under certain regularity conditions,[4] then the Fisher information may also be written as[5]
- {\displaystyle {\mathcal {I}}(\theta )=-\operatorname {E} \left[\left.{\frac {\partial ^{2}}{\partial \theta ^{2}}}\log f(X;\theta )\right|\theta \right],}
![{\displaystyle {\mathcal {I}}(\theta )=-\operatorname {E} \left[\left.{\frac {\partial ^{2}}{\partial \theta ^{2}}}\log f(X;\theta )\right|\theta \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d21830494acf6fa8b7a42febe29b2a7ead86af8)
since
- {\displaystyle {\frac {\partial ^{2}}{\partial \theta ^{2}}}\log f(X;\theta )={\frac {{\frac {\partial ^{2}}{\partial \theta ^{2}}}f(X;\theta )}{f(X;\theta )}}-\left({\frac {{\frac {\partial }{\partial \theta }}f(X;\theta )}{f(X;\theta )}}\right)^{2}={\frac {{\frac {\partial ^{2}}{\partial \theta ^{2}}}f(X;\theta )}{f(X;\theta )}}-\left({\frac {\partial }{\partial \theta }}\log f(X;\theta )\right)^{2}}
and
- {\displaystyle \operatorname {E} \left[\left.{\frac {{\frac {\partial ^{2}}{\partial \theta ^{2}}}f(X;\theta )}{f(X;\theta )}}\right|\theta \right]={\frac {\partial ^{2}}{\partial \theta ^{2}}}\int f(x;\theta )\,dx=0.}
![{\displaystyle \operatorname {E} \left[\left.{\frac {{\frac {\partial ^{2}}{\partial \theta ^{2}}}f(X;\theta )}{f(X;\theta )}}\right|\theta \right]={\frac {\partial ^{2}}{\partial \theta ^{2}}}\int f(x;\theta )\,dx=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34b6bb2ba863b0a3130736fb32d7320c433d4645)
扔了一堆链接，有空整理一下。
然后知道了Laplace Approximation，为啥论文里用的是$F_i$呢，似乎没有用别的偏导啊？
因为 EWC uses a diagonalised Laplace approximation, which ignores the off-diagonal entries of the Hessian and keeping only diagonal ones. Applied to neural networks, the diagonal assumption is the same as saying that the parameters of the network have completely independent influence on the loss function (which is of course not true, but perhaps true enough).
这个Diagonalized Laplace Approximation是啥，我也没查到更多信息，姑且现在这么用着吧。就当作是 Laplace Approximation的简化版（近似的近似）。
（先把自己的推导贴上来吧，有空再整理）
道理我都懂了，那么对于
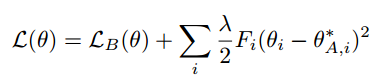
这个费舍尔信息又该咋求呢？
看看Continuous那篇论文里说的meta-learner的训练的那篇论文里有没有答案吧。
估计，是用TaskA的负损失-Loss去近似$p(\theta_A)$，即用TaskA的负损失对参数$p(\theta_A)$求二阶偏导，进而得到费舍尔信息/海森矩阵。
参考资料：
1 https://zhuanlan.zhihu.com/p/25893683 连续学习DeepMind三连
2 https://blog.csdn.net/u010195841/article/details/69257897 EWC笔记
3 https://github.com/ariseff/overcoming-catastrophic 论文EWC复现
4 https://www.inference.vc/comment-on-overcoming-catastrophic-forgetting-in-nns-are-multiple-penalties-needed-2/ 超级大牛的Comment，我的主要参考文献
