图解：如何实现最小生成树（Prim算法与Kruskal算法）

如何理解与实现最小生成树呢？Prim算法与Kruskal算法背后的思想又是怎么样的呢？一起来探索吧~

文章目录：

• 1.概念和性质
• 2.思路探索
• 3.Kruskal算法
• 4.Prim算法
• 5.代码实现

1.概念和性质

今天我们考虑的模型是加权无向图，问题是如何获取它的一幅最小生成树！首先，我们给出最小生成树的定义：

图的生成树是它的一棵含有其所有顶点的无环连通子图。一幅加权图的最小生成树（MST）是它的一棵权值（树中所有边的权值之和）最小的生成树。

如图所示：

首先，我们给出一些约定来简化问题（这并不会影响我们理解问题）

• 只考虑连通图（如果不连通的话是不存在最小生成树的）
• 边的权重可能是0或者负数
• 所有边的权重各不相同（我们给出这个假设之后对于一幅图来说只存在唯一的最小生成树，这样方便我们理解，但是如果把这个限制条件去掉，我们之前得到的算法依然有效😎）

简而言之，我们的讨论对象是一幅权重各不相同的加权无向图，任务是求最小生成树的每条边。接下来，我们一起思考如何实现这个算法！

2.思路探索

---

1）我们的任务是求得最小生成树的每条边，也就是我只要确定了这些边，自然而然也就唯一确定了最小生成树；那么，一棵最小生成树有多少条边呢？我们先来回顾一下树的两个性质：

• 用一条边连接树中的任意两个顶点都会产生一个新的环
• 从树中删去一条边将会得到两棵独立的树

因为一共有V个顶点，生成树的边恰好连接所有顶点（不多不少），所以生成树必定有V-1条边。好了，恭喜你！🙃到这里我们已经前进了一小步！

2）接下来，我说一句话你看是不是对的：

只要找到属于最小生成树的V-1条边（无论什么手段），也就解决了这个问题

你肯定会说，这不是显然的吗？对！但这个是我们向前走的基本思想。记牢了🤓

3）接下来，我们就要寻找一种条件，只要一条边满足这个条件，那么我们就能够断言这条边肯定在最小生成树中。一旦存在，我们就可以通过创造这种条件找到属于最小生成树的边，将它标记；反复创造上述条件，就可以反复地标记边；直到我们标记了V-1条边！ 你是不是惊奇地发现：我们已经成功地解决了这个问题！

4）我们的任务变成了如何寻找与制造这种条件。站在巨人的肩膀上，我们只需要理解就行了😂。这个条件，我们称之为切分定理。

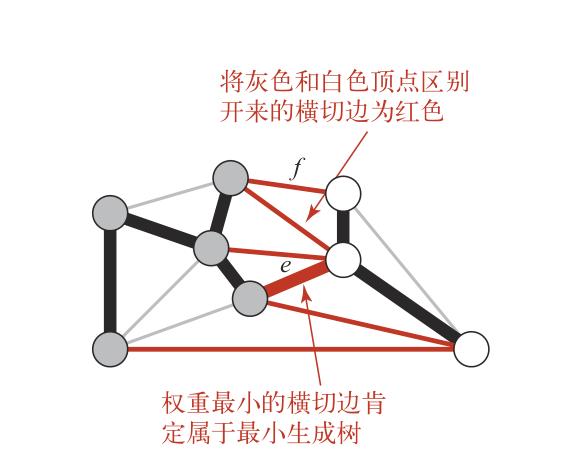
6）我们随意将一幅加权图分为两个非空的集合，横跨两个集合的一条边被称为横切边。而横切边中最短的那个必定属于最小生成树！ 如图所示：

所有的灰色顶点是一个集合，所有的白色顶点是另外一个集合，横跨两个集合的所有的边称为横切边（用红色标出）；其中权重最小的横切边必定属于最小生成树！

这个定理其实很容易想明白，因为这两个集合之间必须要存在且只能存在一条边；如果存在的不是这条最短横切边，那它就不是最小生成树了！请注意一条很重要的性质：这种划分是任意的！
——————我们随便怎么划分都无所谓！这就为处理问题带来了很强的灵活性！

7）我们随后介绍一种通用的算法思想：贪心算法（其实我们在前文已经接触过）。

使用切分定理找到最小生成树的一条边，不断重复直到找到最小生成树的所有边（V-1条即可）

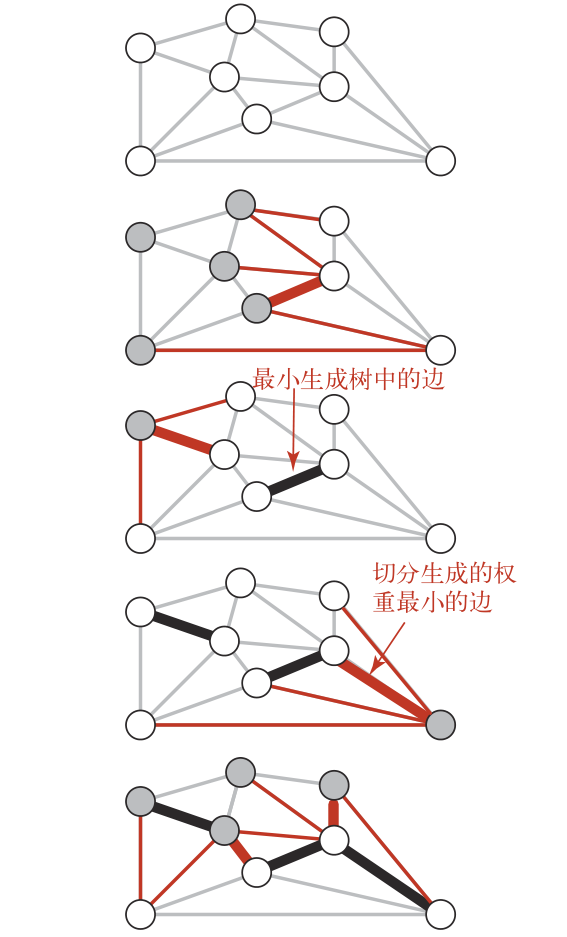
这是一幅贪心算法的执行过程，每次都是将所有顶点分成两个集合（注意：这是任意的！！），然后取最小的横切边加入最小生成树。如此反复，最终就达到了我们的目的！

8）接下来再往后，我们将真正地实现这种算法，而不是只停留在思想上（talk is cheap，show me the code！😍）

• Kruskal算法
• Prim算法地两种形式

3.Kruskal算法

1）我们接着刚才的思路继续，我们面临着两个问题：切分与找到最小横切边；对于切分，由于是随意的，所以还是很容易实现的；另一个问题：怎样很自然地找到最小的横切边呢？

2）一个比较容易想到的解决方案是：

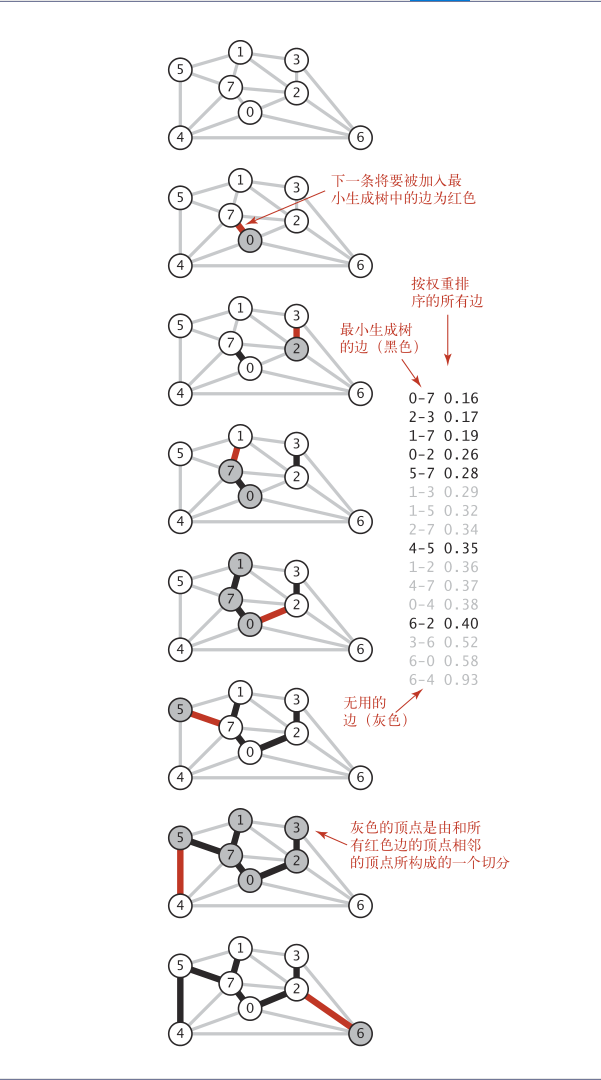
按照边的权重顺序（从小到大）处理他们；
首先，将最小的边加入最小生成树，然后从小到大依次加入边，（注意：待加入的边不能和已经加入的边构成环）；一直重复上述过程直到树中含有V-1条边为止

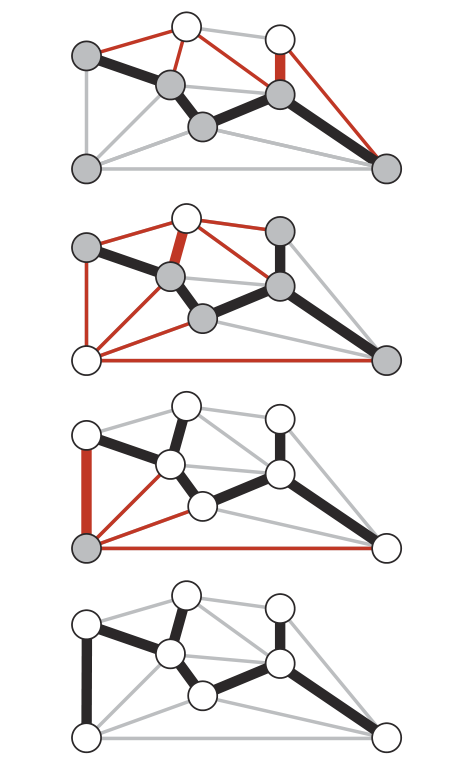
3）现在我们仔细思考一下这个方法。只要待加入的边和已经加入的边没有构成环，就说明这条边是一条横切边，同时，得益于我们加入的顺序（从小到大），我们可以确定这条待加入的边是最小横切边，那么它一定属于最小生成树，将它加入也就没有什么毛病了。来看一下下面的过程：

我们在实现的时候使用了一条优先队列来将边按照权重排序；用前几篇文章中实现的判断无向图连通性的类判断是否连通；用一条队列来保存最小生成树的所有边；就可以很容易实现Kruskal算法。

4.Prim算法

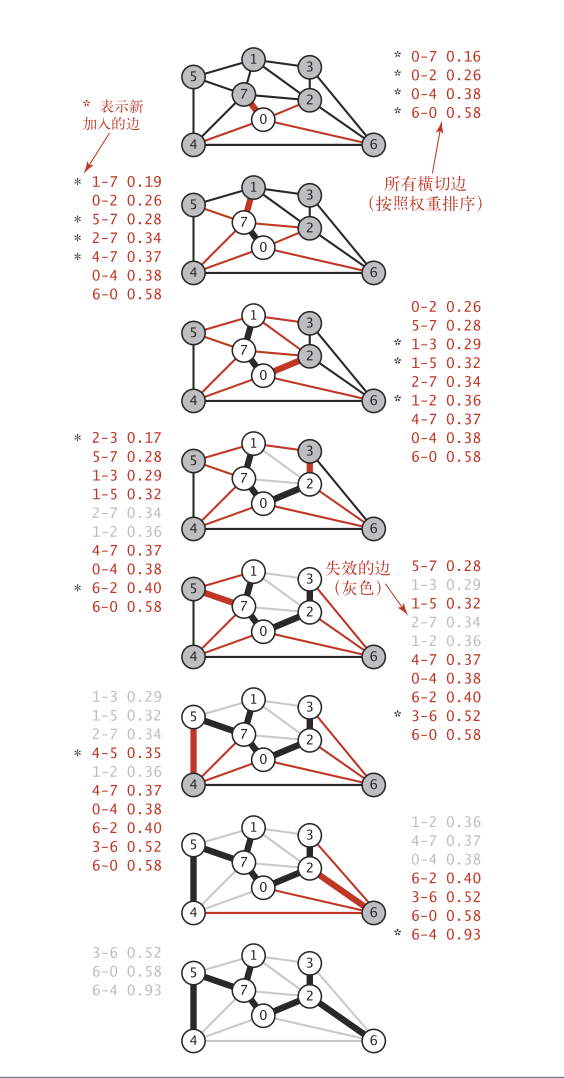
Prim算法的思想与Kruskal算法乍一看有所不同，但是最终你会发现，只是在寻找最小权重的横切边这里使用了不同的 策略罢了。

1）我们考虑这样一种方案：维护一棵生长中的树

• 初始化：将一个顶点（随意，记为A）添加到最小生成树中
• 找到与最小生成树相连的权重最小的一条边（一个顶点在树中，一个顶点不在），并将这条边和相应的顶点加入到最小生成树中
• 重复上述操作，直到所有顶点都被添加

2）这个过程比Kruskal更加简明——————与最小生成树相连的权重最小的一条边；我们把已经在树中的点记为集合A，所有没有在树中的顶点记为集合B，显然我们选择的那条边就是最小横切边！

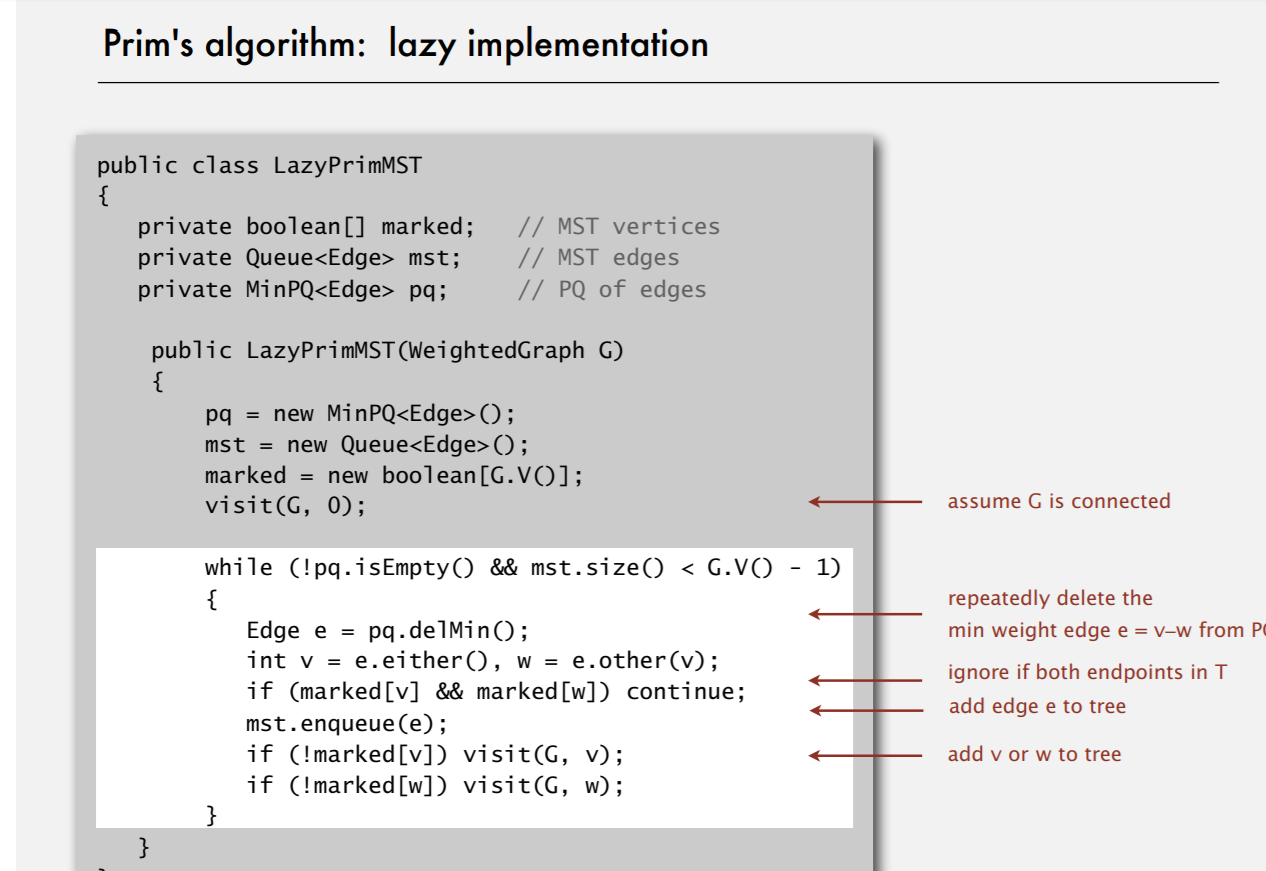
3）虽然过程比较简明，但是实现的代码却不简单，我们需要：

• 顶点。使用一个由顶点索引的布尔数组 marked[]，如果顶点 v 在树中，那么 marked[v] 的值为true
• 边。使用一条队列mst来保存最小生成树中的边
• 横切边：使用一条优先队列 MinPQ<Edge> 来根据权重比较所有边

具体的操作过程如下：

4）到这儿，我们已经实现了Prim算法，它被称为 Prim算法的延时实现 ；但是，还有可以改进的地方，我们可以通过一些改进————删除一些冗余的信息，从而得到Prim算法的即时实现。

5）但是，在这篇文章中，我们就不加以介绍了；它的思想和延时实现一致，目标同样是找到与最小生成树相连的权重最小的一条边，只不过实现方法更加灵活罢了！

5.代码实现

这次和往常不同，我并没有在文章中间掺杂算法的具体实现，我的想法是把它真正的思路讲明白（希望我讲的没有让你失望🤔）；但是，代码还是要有的，我将它们放在了这里，具体来说书籍算法4上面都有！！

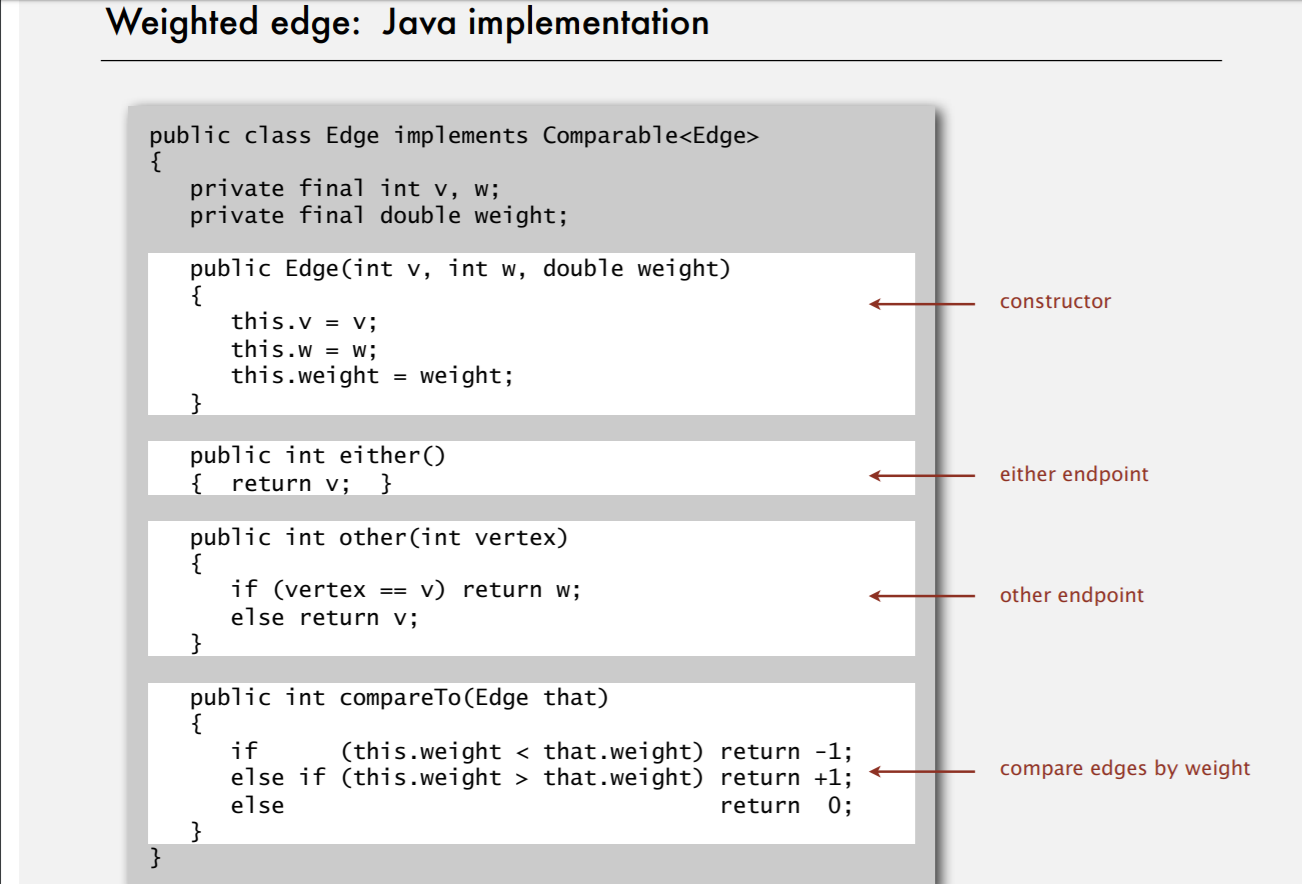
• 如何实现一个加权边
• 如何实现加权无向图
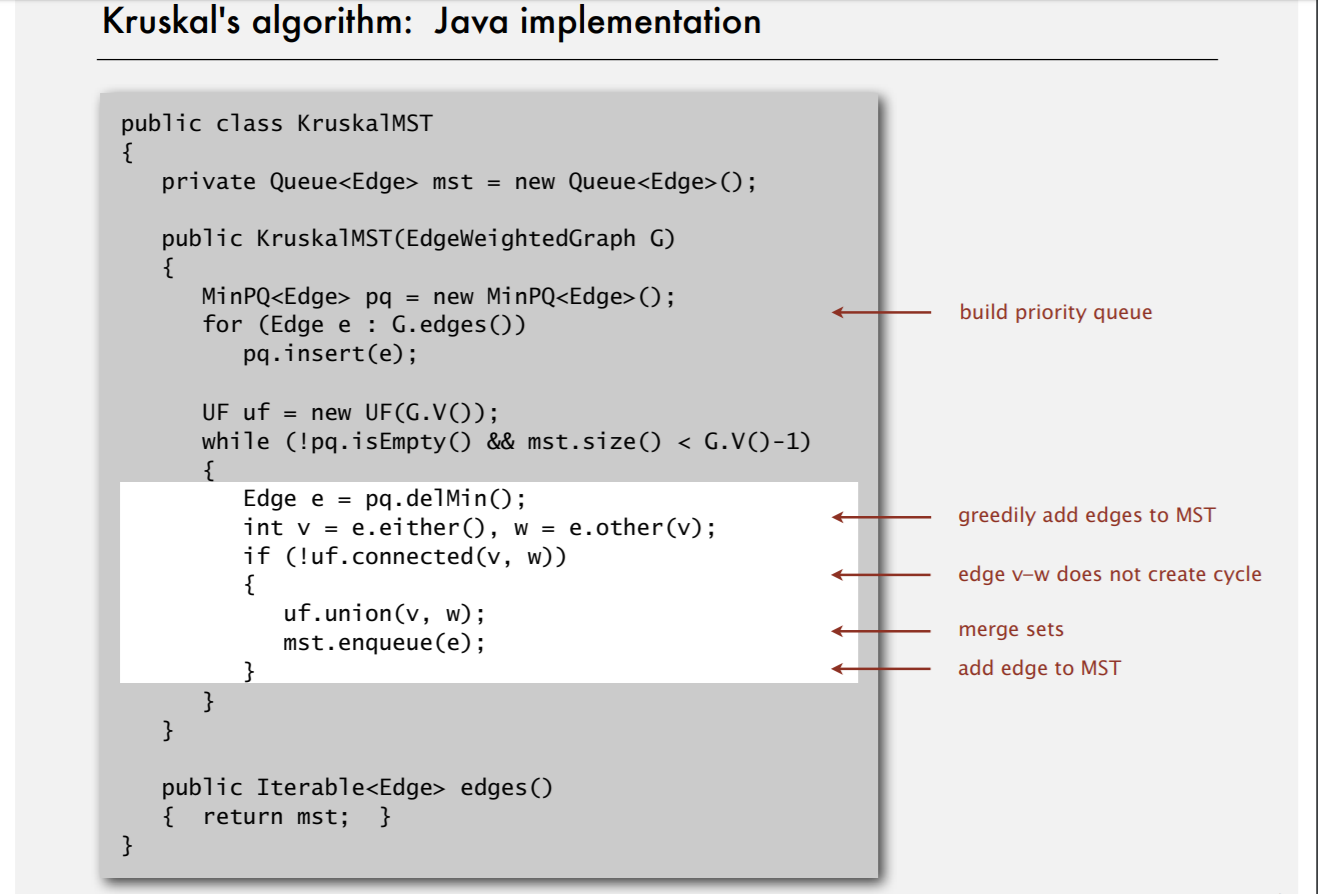
• Kruskal算法的实现
• Prim算法的实现

如何实现一个加权边

如何实现加权无向图

Kruskal算法的实现

Prim算法的实现（两张图片）

全文完