MPLR: a novel model for multi-target learning of logical rules for knowledge graph reasoning

MPLR:知识图推理逻辑规则多目标学习的新模型

摘要

大规模知识图(KGs)提供了人类知识的结构化表示。然而，由于不可能包含所有的知识，kg通常是不完整的。基于已有事实的推理为发现缺失的事实铺平了道路。本文研究了知识图上推理补全缺失事实三元组的逻辑规则学习问题。学习逻辑规则使模型具有较强的可解释性和对类似任务的泛化能力。

---

我们提出了一个名为MPLR的模型，该模型改进了现有的模型，以充分利用训练数据，并考虑了多目标场景。此外，考虑到在评价模型性能和挖掘规则质量方面存在的不足，我们进一步提出了两个新的指标来帮助解决这个问题。实验结果表明，我们的MPLR模型在5个基准数据集上的性能优于目前最先进的方法。结果也证明了指标的有效性。

本文贡献

本文在借鉴以往图论研究的基础上，首先提出了两个新的指标饱和和分叉，这两个指标有助于KG推理任务中的评价。饱和有助于间接分析学习规则的可解释性，而分叉服务是对传统度量的补充。

---

然后我们探索多目标概率逻辑推理(MPLR):神经线性规划框架的扩展，允许在多目标情况下进行推理。我们的方法重新制定了方程，并改进了实体表示和模型优化，这使它能够学习KG中的更多事实。

---

我们将这些指标应用于几个知识图基准，以便更好地理解它们的数据结构。此外，我们在这些数据集上评估了我们的模型，实验表明，我们的模型优于最先进的KG推理方法。此外，MPLR能够生成高质量的逻辑规则。

饱和度定义

宏观推理饱和度

我们将宏观推理饱和度定义为查询子图中所涉及到的三元组所占全部三元组的百分比，公式如下：

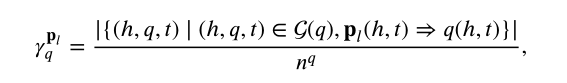
分子是查询子图中涉及到的三元组数，分母是所有三元组（所有的边）数。

微观推理饱和度

公式如下：

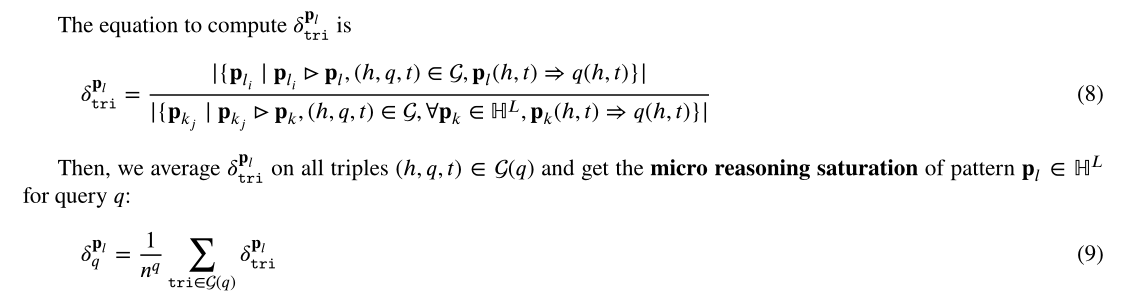
分叉

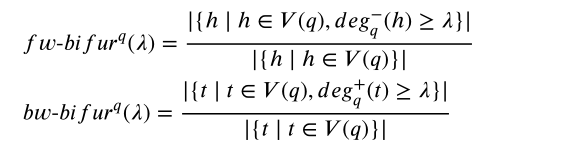
分为入度分叉和出度分叉。入度分叉指入读超过一个定值的头节点所占的百分比，出度分叉指出度超过一个定值的尾节点所占的百分比。

TensorLog

本质是在某一个关系P下的邻接矩阵,边权为1，如p为daughterOf，并且KG表示如下：

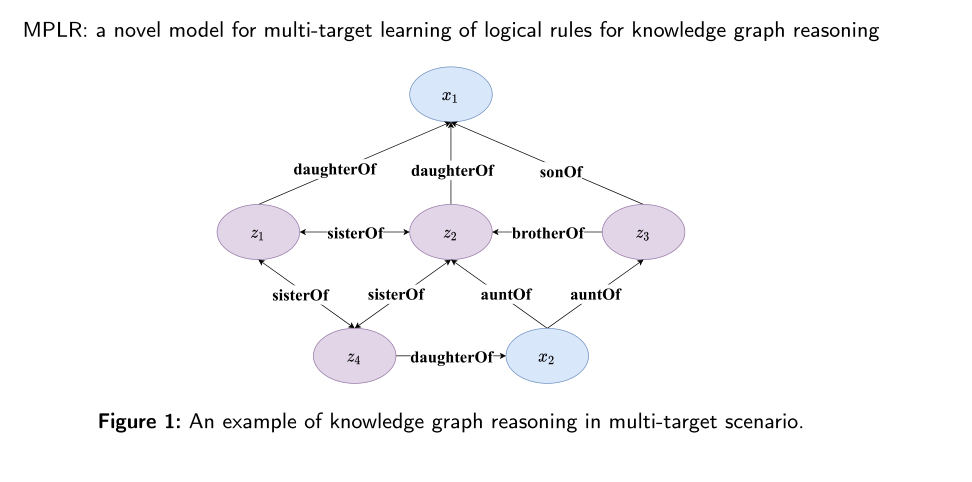
则对应的TensorLog构造为：先将节点集变成邻接矩阵的下标索引，当两个节点(标记为i,j)存在关系P，则对应的的矩阵(i,j)值为1，其余为0。对于上图所属的KG，TensorLog矩阵如下：

(x1, z1)，(x1, z2), (x2, z4)为四个daughterOf关系的三元组。

MPLR model

MPLR模型是对Neural LP模型的改进。在多目标查询中，后者需要把所涉及到的边全部从图中移除，这将很大程度上破环原图的结构。所以在MPLR模型中，我们不去掉那些相关的边，但是在计算查询分数时并不加上这些边的分数。
由于在多个查询中与同一个头节点相关的尾节点有很多个，我们采用多热编码，及对应节点位置上标为1，其他位置标为0。
模型整体结构如下：

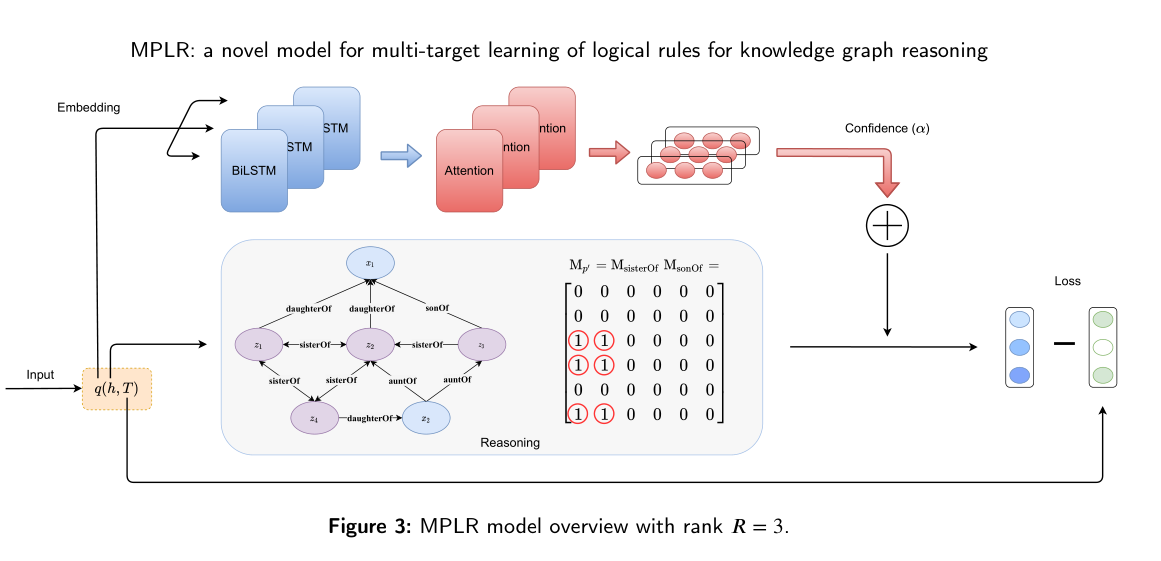
模型性能

模型测试对比结果如下：

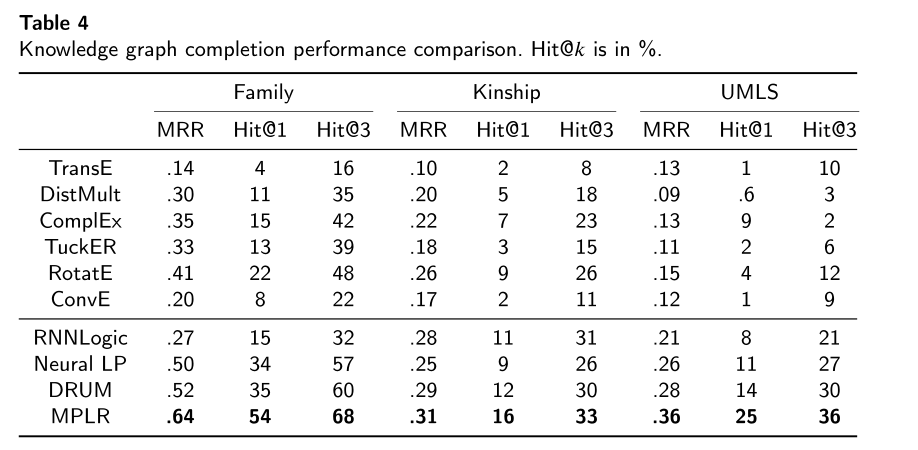
我们的MPLR在表4中列出的所有方法的数据集上的所有指标上都达到了最先进的结果，因为我们可以看到几乎所有数据集都有明显的改进。我们推测，这是由于优化使我们的模型能够一次利用更多的训练数据，以及在多目标情况下的进步。