动态规划

动态规划 Dynamic Programming

一种设计的技巧，是解决一类问题的方法

dp遵循固定的思考流程：暴力递归 —— 递归+记忆化 —— 非递归的动态规划（状态定义+转移方程）

 

斐波那契数列

暴力递归，看上去很简洁

def fib(n):
    return n if n <= 1 else fib(n-1) + fib(n-2)

 

画出递归树分析一下，可以很容易发现有很多重复计算。重叠子问题。

递归算法的时间复杂度怎么计算？子问题个数乘以解决一个子问题需要的时间。显然，斐波那契数列的递归解法时间复杂度为O(2ⁿ * 1)，暴力递归解法基本都会超时。

 

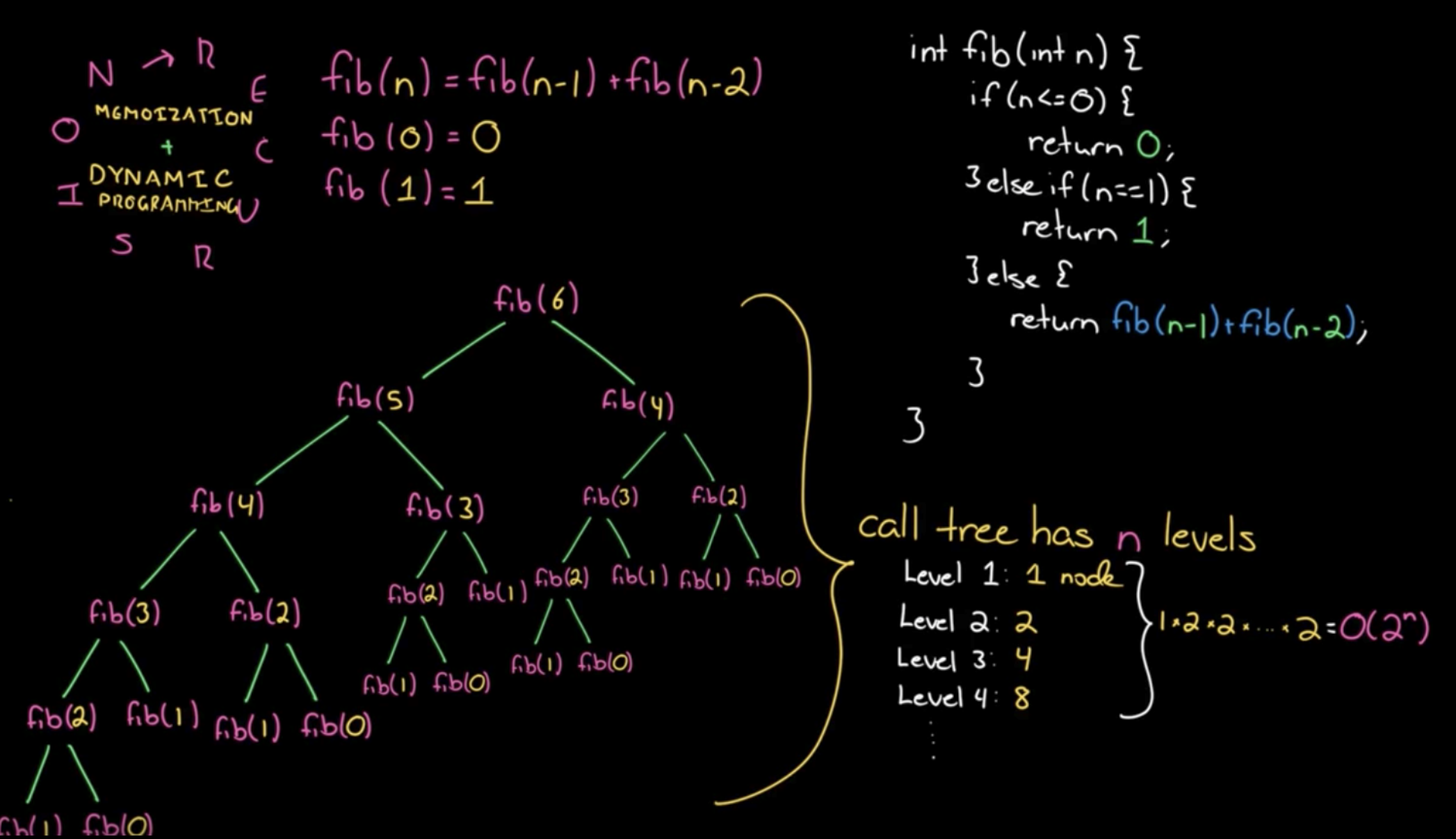
如何解决？递归 + 记忆化

仍然使用递归，不同点在于，如果重叠子问题已经计算过，就不用再算了，相当于对冗余的递归树进行了剪枝。

由于不存在重叠子问题，时间复杂度为O(n * 1)，降到线性。

class Solution:
    def Fibonacci(self, n):
        # write code here
        if n <= 1:
            return n
        memo = [-1] * (n+1)
        memo[0], memo[1]= 0, 1
        
        def helper(n, memo):
            if memo[n] >= 0:
                return memo[n]
            memo[n] = helper(n-1, memo) + helper(n-2, memo)
            return memo[n]
        
        return helper(n, memo)

 

实际上这已经和动态规划一样了，只不过这是自顶向下的。而动态规划是自底向上的。从最小的子问题一步一步向上递推，O(n)

class Solution:
    def Fibonacci(self, n):
        # write code here
        if n <= 1:
            return n
        dp = [0] * (n+1)
        dp[0], dp[1] = 0, 1
        for i in range(2, n+1):
            dp[i] = dp[i-1] + dp[i-2]
        return dp[n]

 

进一步优化空间复杂度，由于只要最后一个状态，而且状态转移只取决于相邻的状态，不需要开一维数组，直接两个变量滚动更新就行了。

class Solution:
    def Fibonacci(self, n):
        # write code here
        if n <= 1:
            return n
        dp_0, dp_1 = 0, 1
        for i in range(2, n+1):
            dp_0, dp_1 = dp_1, dp_0 + dp_1
        return dp_1

 

从一道题展开

最长公共子序列 LCS

给定长度为 m 和 n 的两个数组 x 和 y，找出最长的公共子序列（可能有多个）

x : ABCBDAB

y : BDCABA

存在3个最长公共子序列，长度为4，分别为 BDAB、BCAB、BCBA

 

1. 穷举，穷举x中的所有子序列，再检查y里面是不是也有一样的子序列

　　假设给定了一个子序列，检查它是否为 y 的子序列的复杂度？O(n)，按顺序把 y 对着给定的子序列往后捋一遍即可

　　x 有多少子序列？2^m ，每个元素都可以选或者不选。

　　所以穷举的时间复杂度，O(n2^m)，指数级

 

2. 先确定 LCS 的长度，再看看具体有哪些公共子序列达到了这个长度

　　只要考察前缀即可。定义 c[i, j] 表示 x[1...i] 和 y[1...j] 的 LCS 长度，c[m, n] 就为x 和 y 的 LCS 长度。

　   base cases: c[*, 0] = 0 且 c[0, *] = 0。此外，当 x[i] == y[j] 时，c[i, j] = c[i-1, j-1] + 1；否则 c[i, j] = max(c[i, j-1], c[i-1, j])。这里比较好理解，稍微想一下就清楚了，x[i] 和 y[j] 相等的时候，这个值可以直接算到 LCS 中，所以加1。否则的话，就看看x[i] 和 y[j] 各自算进去哪种情况的 LCS 大。

　　上面结论的一点证明：x[i] == y[j] 时，令 z[1...k] = LCS(x[1...i], y[1...j])，显然 k = c[i, j]。z[k] 就是 x[i] 同时也为 y[j] ，显然一定有 z[1...k-1] = LCS(x[1...i-1], y[1...j-1]) ，c[i-1, j-1] = k-1，即 c[i, j] = c[i-1, j-1] + 1 ；x[i] != y[j] 时的证明类似。

 

由此引出动态规划的第一个特征，最优子结构，指的是问题的一个最优解包含了子问题的最优解。

If z = LCS(x, y),  then any prefix of z is an LCS(a prefix of x ,  a prefix of y).

 

递归实现一下 LCS 计算长度

def LCS(x, y, i, j):
    """ignore base cases"""
    if x[i] == y[j]:
        c[i, j] = LCS(x, y, i-1, j-1) + 1
    else:
        c[i, j] = max(LCS(x, y, i-1, j), LCS(x, y, i, j-1))
    
    return c[i, j]

　　

考虑一下这个递归树，最坏情况下每次都要走取 max 的分支，递归树深度为 m+n，时间复杂度为 O(2^m+n)。可以发现有很多重复计算。由此引出动态规划的第二个特征，重叠子问题。

 

LCS 问题的子问题有 m*n 个，每次算好了就存下来，备忘法

def LSC(x, y, i, j):
    if c[i, j] != None:
        return c[i, j]

    if x[i] == y[j]:
        c[i, j] = LCS(x, y, i-1, j-1) + 1
    else:
        c[i, j] = max(LCS(x, y, i-1, y), LCS(x, y, i, j-1))
    
    return c[i, j]

　　

这个计算所需要的时间？O(m*n)，因为摊销之后每个子问题都只需要执行常数次计算得到结果

空间？O(m*n)，建表

 

自底向上地计算表格　　——动态规划

def lcs_length(x, y):
    if not x or not y:
        return 0
    m, n = len(x), len(y)
    dp = [[0]*(n+1) for _ in range(m+1)]
    
    for i in range(m+1):
        for j in range(n+1):
            if i == 0 or j == 0:
                dp[i][j] = 0
            elif x[i-1] == y[j-1]:
                dp[i][j] = dp[i-1][j-1] + 1
            else:
                dp[i][j] = max(dp[i-1][j], dp[i][j-1])
    
    return dp[-1][-1]

 

优化空间复杂度，比较简单的做法就是用滚动数组优化到 O(2*min(m, n)) ，因为每次都需要查看 dp 表的上一行和这一行的左边。

def lcs_length(x, y):
    if not x or not y:
        return 0
    m, n = len(x), len(y)
    if n > m:
        m, n, x, y = n, m, y, x
        
    dp = [[0]*(n+1) for _ in range(2)]
    
    pre, now = 0, 1
    for i in range(1, m+1):
        pre, now = now, pre
        for j in range(1, n+1):
            if x[i-1] == y[j-1]:
                dp[now][j] = dp[pre][j-1] + 1
            else:
                dp[now][j] = max(dp[pre][j], dp[now][j-1])
                
    return dp[now][-1]

 

在得到 LCS 长度的同时如何得到子序列？根据 dp 表回溯，走到每个位置的时候记录一下从哪里来的。整道题的答案就搞定了

def lcs_length(x, y):
    if not x or not y:
        return 0
    m, n = len(x), len(y)
    dp = [[0]*(n+1) for _ in range(m+1)]
    
    # 1:左上、2:上、3:左、4:上或左
    states = [[0]*(n+1) for _ in range(m+1)]
    
    for i in range(1, m+1):
        for j in range(1, n+1):
            if x[i-1] == y[j-1]:
                dp[i][j] = dp[i-1][j-1] + 1
                states[i][j] = 1
                
            elif dp[i-1][j] > dp[i][j-1]:
                dp[i][j] = dp[i-1][j]
                states[i][j] = 2
                
            elif dp[i-1][j] < dp[i][j-1]:
                dp[i][j] = dp[i][j-1]
                states[i][j] = 3
            else:
                dp[i][j] = dp[i][j-1]
                states[i][j] = 4
                
    lcsLength = dp[-1][-1]            
    printAllLCS(states, x, lcsLength, m, n, '')           
    return lcsLength

def  printAllLCS(states, x, lcsLength, i, j, lcs):
    """states表；只需要一个字符串就够了；LCS长度；当前位置ij；已搜索轨迹lcs"""
    if i == 0 or j == 0:
        if len(lcs) == lcsLength:
            print(lcs[::-1])  # 从后往前dfs搜索的，这里逆序输出
        return
    
    direction = states[i][j]
    if direction == 1:
        printAllLCS(states, x, lcsLength, i-1, j-1, lcs+x[i-1])
    elif direction == 2:
        # 同一行或者同一列转移过来的字符没有变化
        printAllLCS(states, x, lcsLength, i-1, j, lcs)
    elif direction == 3:
        printAllLCS(states, x, lcsLength, i, j-1, lcs)
    elif direction == 4:
        # 两个来源都有可能
        printAllLCS(states, x, lcsLength, i-1, j, lcs)
        printAllLCS(states, x, lcsLength, i, j-1, lcs)

 

 

带权项目时间计划

典型的选还是不选的问题。OPT(i) 表示一共有前 i 个任务的话，最多能挣多少钱，那么从后往前考虑，就是第i个任务选还是不选。如果不选，OPT(i) = OPT(i-1)；如果选了，就看选了第i个，再往前有几个能做，比如如果选了8，那么前面只能从5往前选，用prev(i)来表示这个索引，即prev(8) = 5。所以递推公式已经列出来了，而prev(i)是可以先确定的。

 

写出递归树可以发现这是个重叠子问题，用动态规划求解即可。

 

 

和最大的不连续子数组

给定一个数组，选出和最大的子数组，长度不限，但不能选相邻元素。例如 [4, 1, 1, 9, 1]，满足条件的和最大子数组为 [4, 9]。定义 OPT(i) 为到下标为 i 的数为止的最大不连续子数组之和。如果选了下标为 i 的数，那么前面最多能选到下标 i-2；如果不选则前面能选到 i-1

def maxSubArray(arr):
    if not arr:
        return 0
    
    n = len(arr)
    if n == 1:
        return arr[0]
    
    dp = [0]*n
    dp[0], dp[1] = arr[0], max(arr[0], arr[1])
    
    for i in range(2, n):
        dp[i] = max(dp[i-2] + arr[i], dp[i-1])
        
    return dp[n-1]

 

 

和为给定值的子数组

给定一个正整数数组和一个正整数目标值，判断能否找到一个子数组，和恰好为给定的目标值。subset(i, s)，i表示当前看第i个数字、s为目标值。对于每个当前数字，有选或不选两种可能，只要有一种满足条件即可。

出口情况：s为0，返回 true；i为0，只有当 s == arr[0] 才返回true；如果 arr[i] > s，选上一定超，只考虑不选arr[i]的情况

if s == 0:
    return True
if i == 0:
    return arr[i] == s
if arr[i] > s:
    return subset(i-1, s)

　　

递归写一下

def solution(array, s):
    if not array:
        return False
    n = len(array)
    
    def helper(arr, i, s):
        if s == 0:
            return True
        if i == 0:
            return arr[i] == s
        if arr[i] > s:
            return helper(arr, i-1, s)
        return helper(arr, i-1, s-arr[i]) or helper(arr, i-1, s)
    
    return helper(array, n-1, s)

 

动态规划写一下，显然是一个二维 dp，递归出口就是 dp 的初始化的条件

def solution(array, s):
    if not array:
        return False
    n = len(array)
    dp = [[False]*(s+1) for _ in range(n)]
    
    for i in range(n):
        dp[i][0] = True
        
    dp[0][array[0]] = True
    
    for i in range(1, n):
        for t in range(1, s+1):
            if array[i] > t:
                dp[i][t] = dp[i-1][t]
            else:
                dp[i][t] = dp[i-1][t-array[i]] or dp[i-1][t]
    return dp[-1][-1]

 

 

零钱兑换

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

暴力法，先考虑一下递归关系。 总金额为0时，f(amount) = 0；总金额不为0时，f(amount) = 1 + min{ f(amount - ci) | i 属于 [1, k] }。

解释一下，要求总金额为amount的最少硬币个数，先选一个合法可选面值的硬币，总金额变为amount - ci，总的最少硬币数等于子问题的最优解+1。

这里用到了最优子结构性质，即原问题的解由子问题的最优解构成。要符合最优子结构，子问题之间必须独立。

import sys
class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        if amount == 0:
            return -1
        ans = sys.maxsize
        for coin in coins:
            if amount < coin:  # 金额不可达
                continue
            subProblem = self.coinChange(coins, amount-coin)
            
            if subProblem == -1:  # 子问题无解
                continue
            ans = min(ans, subProblem + 1)
        
        return -1 if ans == sys.maxsize else ans

 

递归+记忆化

import sys
class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        if not coins:
            return -1
        memo = [-2] * (amount+1)   # memo[amount]表示凑到金额为amount的最少硬币数
        
        def helper(coins, amount, memo):
            if amount == 0:
                return 0
            if memo[amount] != -2:
                return memo[amount]
            
            ans = sys.maxsize
            for coin in coins:
                if amount < coin:  # 金额不可达
                    continue
                subProblem = helper(coins, amount-coin, memo)

                if subProblem == -1:  # 子问题无解
                    continue
                ans = min(ans, subProblem + 1)
            
            memo[amount] = -1 if ans == sys.maxsize else ans  # 记录本轮答案
            return memo[amount]  
        
        return helper(coins, amount, memo)

 

动态规划，按上面描述的状态方程。

import sys
class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        if not coins:
            return 0
        dp = [sys.maxsize] * (amount+1)
        dp[0] = 0
        
        for i in range(1, amount+1):
            for j in range(len(coins)):
                if i < coins[j]:
                    continue
                dp[i] = min(dp[i], dp[i - coins[j]] + 1)
            
        return -1 if dp[amount] == sys.maxsize else dp[amount]

 

 

出发到终点所有可能的路径问题

只能向右或向下，涂实的点不能走。考虑每个出发点可能的路径数，等于右边一格作为出发点的路径数+下边一格作为出发点的路径数。

暴力递归，自顶向下

 

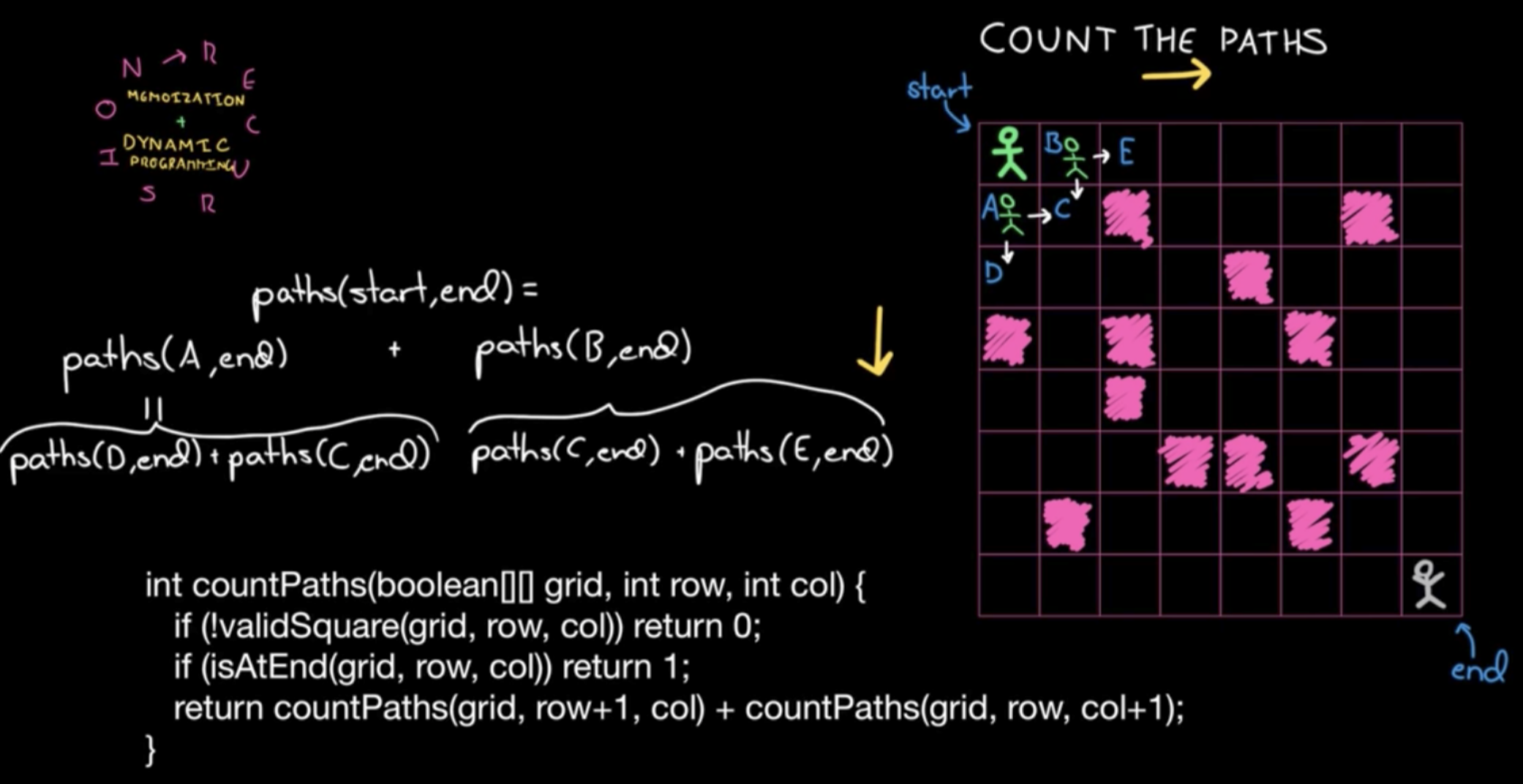
自底向上递推，如果要到达a[i, j]点，只能从它的上面或者左边经过：

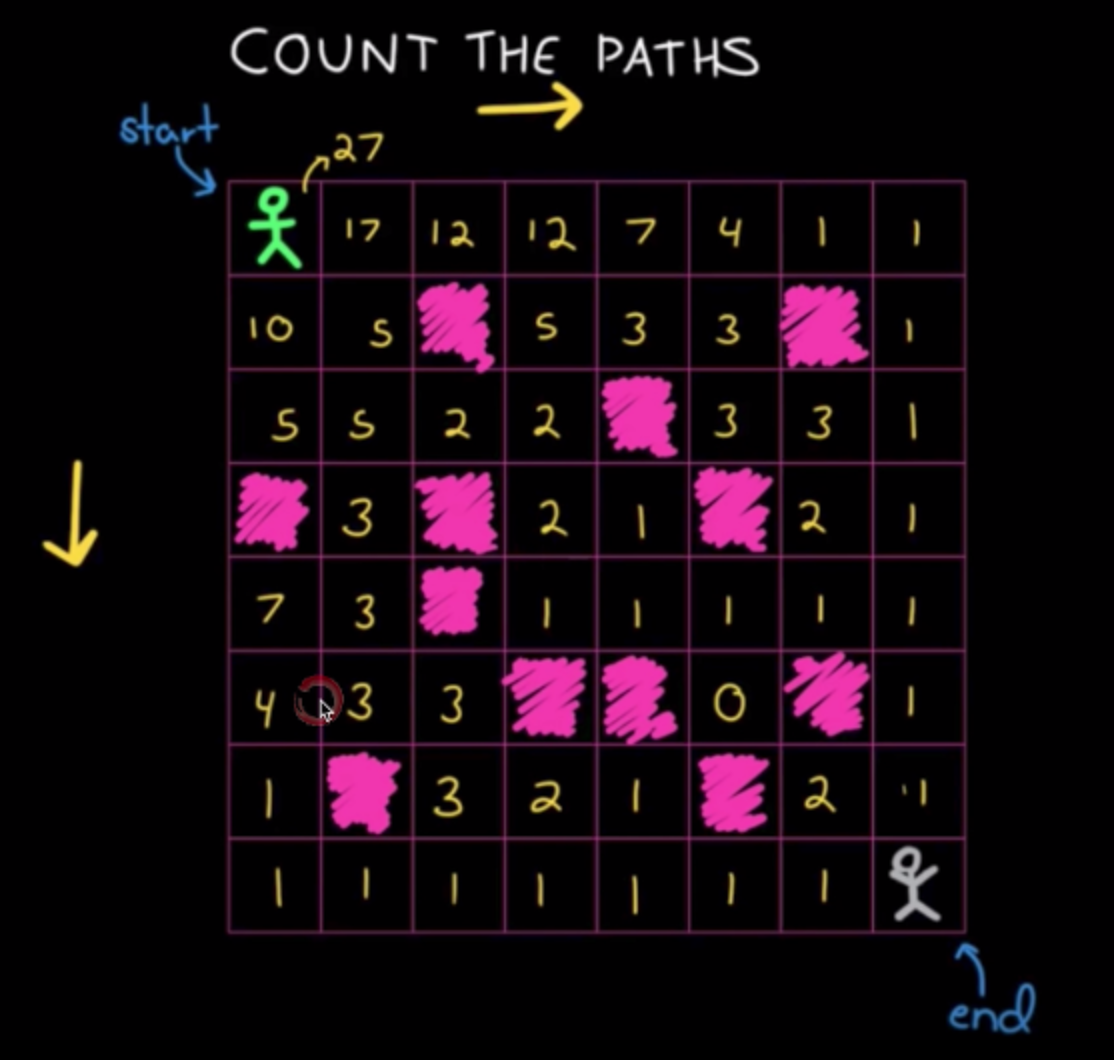
opt[i, j] = opt[i-1, j] + opt[i, j-1]

# --------------------------------------

if isValid(a[i, j]):
    opt[i, j] = opt[i-1, j] + opt[i, j-1]
else:
    opt[i, j]  = 0   # 石头

　

 

正则表达式

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

说明:

s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *。

先看不管通配符，两个普通字符串进行比较应该怎么写。然后再改成比较通用的框架，再写成递归

def isMatch(text, pattern):
    if len(text) != len(pattern):
        return False
    for j in range(len(pattern)):
        if pattern[j] != text[j]:
            return False
    return True

def isMatch(text, pattern):
    m, n = len(text), len(pattern)
    i, j = 0, 0   # 双指针 
    while j < n:
        if i >= m:  # 如果text的指针越界了但pattern的指针没有，说明没有待匹配的字符了但模式串还剩下，不匹配
            return False
        if pattern[j] != text[i]: 
            return False
        j += 1
        i += 1
    return j == n  # 最后看模式串字符是不是都匹配完了

def isMatch(text, pattern):
    if len(pattern) == 0:
        return len(text) == 0
    first_match = len(text) != 0 and text[0] == pattern[0]
    return first_match and isMatch(text[1:], pattern[1:])

 

然后处理通配符，'.' 可以匹配任意一个字符，所以判断能不能匹配的时候有两种情况，直接匹配或者用'.'匹配

def isMatch(text, pattern):
    if not pattern:
        return not text
    first_match = bool(text) and pattern[0] in {text[0], '.'}
    return first_match and isMatch(text[1:], pattern[1:])

 

再处理'*'，星号可以让之前的一个字符出现任意次数，包括0次。关键就是出现几次呢，交给递归好了，当前只可能出现0次或者1次。如果匹配前一个字符0次，那就直接从模式串的p[2:] 再匹配文本串；如果当前匹配一次，那文本串要向后移动一位，后面还需要匹配几次交给递归。

def isMatch(text, pattern):
    if not pattern:
        return not text
    first_match = bool(text) and pattern[0] in {text[0], '.'}
    if len(pattern) >= 2 and pattern[1] == '*':  # '*' 不能放首位，发现'*'
        return isMatch(text, pattern[2:]) or (first_match and isMatch(text[1:], pattern))
    # else
    return first_match and isMatch(text[1:], pattern[1:])

 

然后加上记忆化

def isMatch(text, pattern):
    memo = dict()
    def dp(i, j):
        if (i, j) in memo:
            return memo[(i, j)]
        if j == len(pattern):
            return i == len(text)
        first_match = i < len(text) and pattern[j] in {text[i], '.'}
        if j <= len(pattern)-2 and pattern[j+1] == '*':
            ans = dp(i, j+2) or (first_match and dp(i+1, j))
        else:
            ans = first_match and dp(i+1, j+1)
        memo[(i, j)] = ans
        return ans
    
    return dp(0, 0)

 

 

如何判断是不是重叠子问题：

　　1. 随便假设一个输入，画递归树

　　2. 先抽象出递归算法的框架，然后判断原问题是如何到达子问题的，看看不同的路径是不是都到达了同一个问题，如果是的话那就是重叠子问题。例如这题

def dp(i ,j):
    dp(i, j+2) # 1
    dp(i+1, j) # 2
    dp(i+1, j+1) # 3

　　

dp(i, j) 如何到达 dp(i+2, j+2)。 dp(i, j) -> #3 -> #3；或者dp(i, j) -> #1 -> #2 -> #2；或者dp(i, j) -> #2 -> #2 -> #1，所以一定存在重叠子问题，一定需要动态规划技巧来优化。

def isMatch(text, pattern):
        dp = [[False] * (len(pattern)+1) for _ in range(len(text)+1)]
         
        dp[-1][-1] = True  # 空串匹配空串
        
        for i in range(len(text), -1, -1):
            for j in range(len(pattern)-1, -1, -1):
                first_match = i < len(text) and pattern[j] in {text[i], '.'}
                if j <= len(pattern)-2 and pattern[j+1] == '*':
                    dp[i][j] = dp[i][j+2] or (first_match and dp[i+1][j])
                else:
                    dp[i][j] = first_match and dp[i+1][j+1]
                     
        return dp[0][0]

 

 

设计动态规划的通用技巧：数学归纳

最长递增子序列

给定一个无序的整数数组，找到其中最长上升子序列的长度。

定义 dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度。根据这个定义，子序列的最大长度应该是dp数组中的最大值。假设已经知道了 dp[0...i-1] 的结果，如何通过这些已知结果推出 dp[i] 呢，这个就是状态转移方程了。显然要知道 nums[i] 能不能加入到上升子序列中，就要找到前面那些结尾比 nums[i] 小的子序列，然后再把 nums[i] 接上，因为要求最大子序列，所以就接上之前的最大子序列即可。剩下的就是base case，这题 dp 数组初始化为1，因为子序列最少也要包含自己。

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums:
            return 0
        n = len(nums)
        dp = [1] * n
        for i in range(n):
            for j in range(i-1, -1, -1):
                if nums[j] < nums[i]:
                    dp[i] = max(dp[i], dp[j] + 1)
        return max(dp)

 

但这道题还有一种 O(NlogN) 的解法，但是不看答案估计很难想得出。把上面方法中内层 j 循环替换成二分。始终维护一个数组 LIS 为要求的上升子序列，对每一个 nums[i]，都插入到LIS中（二分法找到第一个比 nums[i] 大的数替换掉，因为这样尽可能多的让后面符合条件的数进来、缩一下上界。如果 nums[i] 比 LIS 所有都大就直接 append），最后 LIS 的长度即为所求。 代码在 Leetcode-动态规划 https://www.cnblogs.com/chaojunwang-ml/p/11365562.html

 

 

从最长上升子序列到信封嵌套

俄罗斯套娃信封问题

这道题是最长上升子序列的升维，要先对宽度进行升序排列，然后对宽度相同的按高度降序排序。最后对高度数组进行最长上升子序列的求解

class Solution:
    def maxEnvelopes(self, envelopes: List[List[int]]) -> int:
        if not envelopes:
            return 0
        n = len(envelopes)
        nums = sorted(envelopes, key=lambda x: [x[0], -x[1]])
        dp = [1] * n
        
        for i in range(n):
            for j in range(i-1, -1, -1):
                if nums[i][1] > nums[j][1]:
                    dp[i] = max(dp[i], dp[j] + 1)
        return max(dp)

　　

用刚才提到的二分法来优化

class Solution:
    def maxEnvelopes(self, envelopes: List[List[int]]) -> int:
        if not envelopes:
            return 0
        n = len(envelopes)
        nums = sorted(envelopes, key=lambda x: [x[0], -x[1]])
        LIS = []
        
        for i in range(n):
            if not LIS or nums[i][1] > LIS[-1]:
                LIS.append(nums[i][1])
            else:
                index = self.binarySearch(LIS, nums[i][1])
                LIS[index] = nums[i][1]
        return len(LIS)
    
    def binarySearch(self, array, target):
        """返回第一个比target大的元素索引"""
        if not array:
            return
        low, high = 0, len(array) - 1
         
        while low <= high:
            mid = low + (high-low)//2
            if array[mid] < target:
                low = mid + 1
            elif array[mid] > target:
                high = mid - 1
            else:
                return mid
        return low

 

 

 

博弈问题的思路是在二维dp的基础上使用元组分别存储两个人的博弈结果。

一堆石头用数组piles表示，piles[i]表示第i堆有多少个石头，两个人拿石头，一次拿一堆，但只能拿走最左边或者最右边。所有石头被拿完后，谁拥有但石头多谁获胜。

假设两人都很聪明，请你设计一个算法，返回先手和后手的最后得分（石头总数）之差。比如上面[1, 100, 3]，先手能获得 4 分，后手会获得 100 分，你的算法应该返回 -96。

博弈问题的通用框架。

定义dp数组，dp[i][j] = (first, second)，dp[i][j].fir 表示对于 piles[i,...,j]这部分，先手能获得的最高分数，dp[i][j].sec 表示后手能获得的最高分数

对于每个状态，可以做的选择有两个：选择最左边的还是最右边的。那么穷举状态：

for 0<=i <n:
    for  i<=j < n:
        for who in {first, second}:
            dp[i][j][who] = max(left, right)

　　

但是先手的选择会对后手有影响。面对piles[i,...,j]先手选了左边，然后面对piles[i+1,...,j]但对方先选，自己变成后手。或者先手选了右边，然后面对piles[i,...,j-1]自己后手。

dp[i][j].fir = max(piles[i] + dp[i+1][j].sec, piles[j] + dp[i][j-1].sec)  

如果作为后手，就要等先手先选择，如果对方先手选了最左边，自己先手面对piles[i+1,...,j]；

dp[i][j].sec = dp[i+1][j].fir

如果对方先手选了右边，自己先手面对piles[i,...,j-1]

dp[i][j].sec = dp[i][j-1].fir

 

那么，base case也容易确定，当i==j，也就是只有一堆的时候，先手得分为piles[i]，后手不得分0。但是 base case 在 dp table 中是斜的，而且计算dp[i][j]的时候需要dp[i+1][j] 和dp[i][j-1]，所以要斜着遍历数组。（怎么实现？按对角线斜线往下，一条一条遍历）

class Pair:
    def __init__(self, fir, sec):
        self.fir = fir
        self.sec = sec
        
def stoneGame(piles):
    if not piles:
        return 0
    n = len(piles)
    dp = [[Pair(-1, -1) for _ in range(n)] for _ in range(n)]
    
    for i in range(n):
        dp[i][i].fir = piles[i]
        dp[i][i].fir = 0
        
    # 斜着遍历
    for l in range(1, n):  # 目前遍历的是第几条斜线，第0条初始化了
        for i in range(n-l):  # dp[i][j]需要dp[i+1][j] 和dp[i][j-1]
            j = l + i  # j的坐标始终比i多l
            left = piles[i] + dp[i+1][j].sec
            right = piles[j] + dp[i][j-1].sec
            
            if left > right:
                dp[i][j].fir = left
                dp[i][j].sec = dp[i+1][j].fir
            else:
                dp[i][j].fir = right
                dp[i][j].sec = dp[i][j-1].fir
                
    return dp[0][n-1].fir - dp[0][n-1].sec

 

 

背包问题

01背包

N 件物品，容量为 C 的背包，第 i 件物品的重量为 Wi，价值为Vi。求装的最大价值

每件物品要么取要么不取。dp[i, j] 表示取到前 i 件物品，容量为 j 的最大价值，

dp[i, j] = max(dp[i-1, j],  dp[i-1, j - Wi] + Vi) i:1~n  j:0~W

 

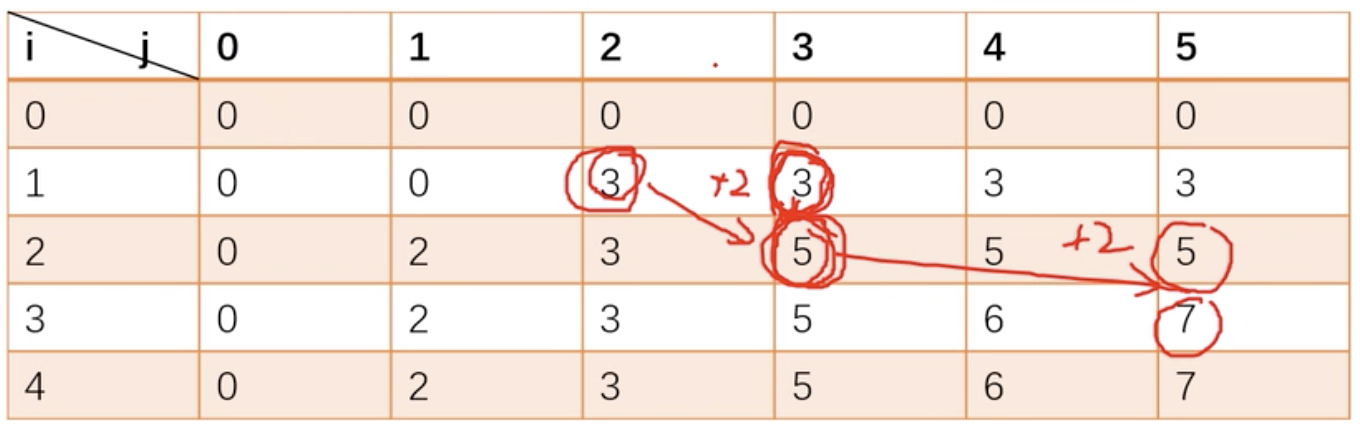
如果倒着遍历，可以用滚动数组把 dp 数组优化到一维，dp[j] = max(dp[j], dp[j-Wi]+Vi)  j:W~0

 

完全背包

N 件物品，容量为 C 的背包，第 i 件物品的重量为 Wi，价值为Vi，每件物品有无数个。求装的最大价值

每件物品可以从不取，一直取到背包满了为止。dp[i, j] 表示取到前 i 件物品，容量为 j 的最大价值，

dp[i, j] = max( dp[i-1, j - k*Wi] + k*Vi  | 0 <= k<= j//Wi  )

 

考虑一下优化，对于 dp[i, j] ，选择 k 个；等价于 dp[i, j-Wi] 选择 k-1 个，这是两个重复计算的状态。

所以把 k=0 的状态提出来，dp[i, j] = max{dp[i-1, j],  dp[i-1, j-k*Wi] + k*Vi, 1<= k <= j//Wi}

dp[i-1, j-Wi-k*Wi] + k*Vi + Vi | 0 <= k <= (j-Wi)//Wi ；对所有的 k 取 max，就等价于 dp[i, j - Wi] + Vi

所以 dp[i, j] = max( dp[i-1, j], dp[i, j - Wi] + Vi)

就得到了 O(CN) 的算法。

 

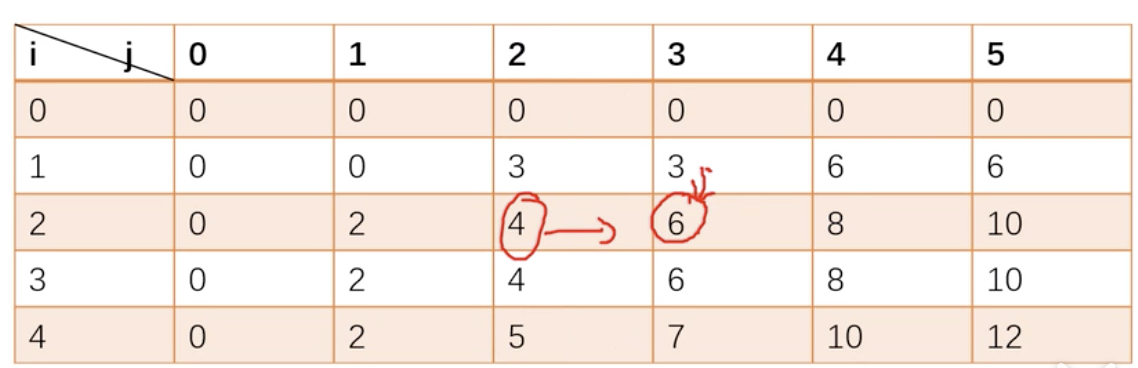
滚动数组优化，但这里要注意的是正着遍历，因为 dp[i, j - Wi] 是当前层的值。dp[j] = max(dp[j], dp[j-Wi]+Vi)  j:0～W

 

硬币兑换

仅有1分、2分、3分的硬币，将钱 N 兑换成硬币有多少种方法。N < 32768

用完全背包的思路来思考，dp[i, j] = dp[i-1, j] + dp[i, j-a[i]]；进一步优化成 dp[j] = dp[j] + dp[j-a[i]]

 

 

DP vs 回溯 vs 贪⼼

回溯(递归) — 重复计算
（没有最优子结构的话就是需要穷举所有的可能，而且不存在重复计算的问题）

贪⼼算法 — 永远局部最优
（但处处局部最优可能最后不是全部最优）

动态规划 — 记录局部最优⼦子结构 / 多种记录值（避免重复计算，只需依赖前一状态的最优值）