6. N 字形变换

题目：

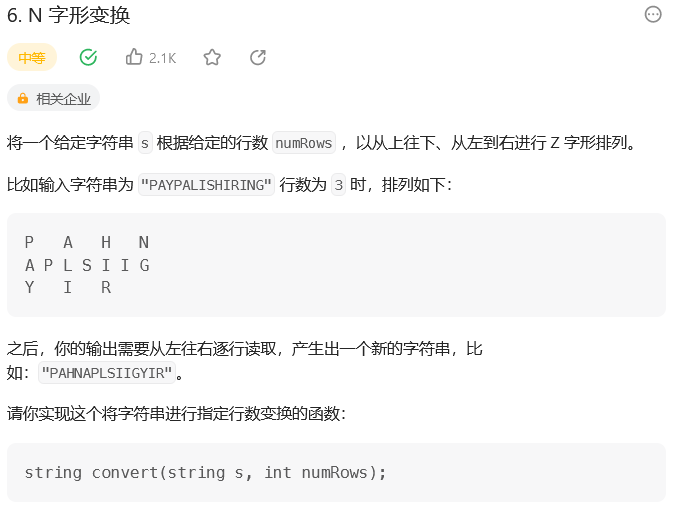
思路：

【1】模拟的方式（采用二维数组，模拟出数据的存放排列，再遍历合成）

【2】按照规律顺序的方式（根据规律逐个放置于新数组中）

代码展示：

//时间80 ms 击败 5.4%
//内存53.1 MB 击败 5.1%
class Solution {
    public String convert(String s, int numRows) {
        int len = s.length();
        String[][] tem = new String[numRows][len];

        int index = 0;
        int offset = numRows-1 > 0 ? numRows-1 : 1;
        // 从左往右遍历
        for (int col = 0;col < len;col++){
            //从上往下遍历
            for (int row = 0;row < numRows;row++){
                // 防止溢出
                if (index == len) break;

                // 列偏移
                int colDif = col%offset;
                // 行偏移
                int rowDif = row%offset;

                // 列偏移 = 0这种情况是这一列都要填数据
                // 列偏移+行偏移 % 偏移数 = 0 的情况便是之字部分
                if (colDif == 0 || (colDif+rowDif)%offset == 0){
                    tem[row][col] = String.valueOf(s.charAt(index++));
                }
            }
            // 如果字符填充完了就跳出循环
            if (index == len) break;
        }

        StringBuffer buf = new StringBuffer();
        for (int row = 0;row < numRows;row++){
            for (int col = 0;col < len;col++){
                if (tem[row][col] != null)
                    buf.append(tem[row][col]);
            }
        }

        return buf.toString();
    }
}


//时间69 ms 击败 5.10%
//内存53.5 MB 击败 5.1%
//时间复杂度：O(r⋅n)，其中 r=numRows，n 为字符串 s 的长度。
//时间主要消耗在矩阵的创建和遍历上，矩阵的行数为 r，列数可以视为 O(n)。
//空间复杂度：O(r⋅n)。矩阵需要 O(r⋅n) 的空间。
class Solution {
    public String convert(String s, int numRows) {
        if (numRows<=1) {
            return s;
        }
        int len = s.length();
        int offset = numRows - 1;
        // 当我们在矩阵上填写字符时，会向下填写 numRows 个字符，
        // 然后向右上继续填写 numRows−2 个字符，最后回到第一行，
        // 因此 Z 字形变换的周期 t=numRows+numRows−2=2numRows−2，
        // 每个周期会占用矩阵上的 1+r−2=r−1 列。
        // 因此有 n/t 个周期（n为字符串长度，最后一个周期视作完整周期,也就是说如果是有余数的话要+1），
        // 乘上每个周期的列数，得到矩阵的列数 c=(n/t)⋅(r−1)
        // [一个周期占用 r-1 列，那么 n/t个周期 占用的列 就是c]。
        int t = 2*offset;
        // 这里之所以 len + t - 1 便是为了考虑java正数相除得整数
        // 如 (3 + 3 - 1) / 3 = 1 而 (4 + 3 - 1) / 3 = 2 (相当于向上取整的操作)
        int colNum = (len + t - 1) / t * offset;
        String[][] tem = new String[numRows][colNum];

        int index = 0;
        // 从左往右遍历
        for (int col = 0;col < colNum;col++){
            //从上往下遍历
            for (int row = 0;row < numRows;row++){
                // 防止溢出
                if (index == len) break;

                // 列偏移
                int colDif = col%offset;
                // 行偏移
                int rowDif = row%offset;

                // 列偏移 = 0这种情况是这一列都要填数据
                // 列偏移+行偏移 % 偏移数 = 0 的情况便是之字部分
                if (colDif == 0 || (colDif+rowDif)%offset == 0){
                    tem[row][col] = String.valueOf(s.charAt(index++));
                }
            }
            // 如果字符填充完了就跳出循环
            if (index == len) break;
        }

        StringBuffer buf = new StringBuffer();
        for (int row = 0;row < numRows;row++){
            for (int col = 0;col < colNum;col++){
                if (tem[row][col] != null) {
                    buf.append(tem[row][col]);
                    index--;
                }
                //如果字符塞完了，就应该停下来
                if (index == 0) break;
            }
        }

        return buf.toString();
    }
}


//时间1 ms击败100%
//内存42.7 MB击败52.53%
class Solution {
    public String convert(String s, int numRows) {
        if (numRows<=1) {
            return s;
        }
        char[] chars = s.toCharArray();
        int index=0;
        char[] newChars = new char[chars.length];
        for (int level = 0; level < numRows; level++) {
            // 这里的精髓在于 i= i + 2*(numRows - 1)
            // 如第一行的表现（可自行画图），这就是能精准的获取下一个字符的位置
            for (int i = level; i<chars.length; i= i + 2*(numRows - 1)) {
                newChars[index++] = chars[i];
                // 因为第一行和最后一行是没有之字的部分的。故跳过
                if (level==0 || level == numRows-1) {
                    continue;
                }
                // 之字部分的填充
                int deep = numRows - level;
                // 要判断不溢出
                if (i + 2*(deep - 1) < chars.length) {
                    newChars[index++] = chars[i + 2*(deep - 1)];
                }
            }
        }
        return new String(newChars);
    }
}