剑指 Offer II 104. 排列的数目（377. 组合总和 Ⅳ）

题目：

 

 

  

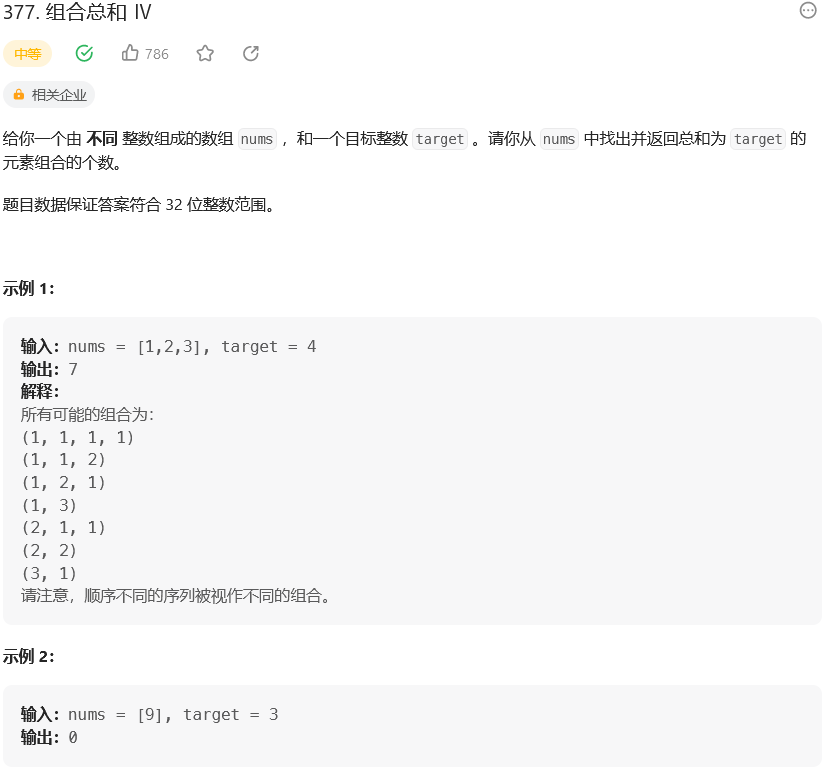
思路：

【1】动态规划的方式：

本质上和  剑指 Offer II 103. 最少的硬币数目（322. 零钱兑换） 这道题十分相似
类似于多少不同金额的硬币凑成了对应的钱
和我们这道选择数值，组合成对应的数值
那么选择的话就是对应的F(N)
如果是【1,2,3】，4
那么F(4) = F(4-1)+F(4-2)+F(4-3);
而且这里存在一个问题就是N不能小于0，因为如果是【1,2,3,5】，目标是4，那么就不能选择5是一个道理。
同理和跳台阶的想法是一样的。

【2】回溯的方式

【3】对于进阶的问题

如果给定的数组中含有负数，则会导致出现无限长度的排列。
如【1，-1】，目标0
那么存在
1-1=0
1+1-1-1=0
1+1+1-1-1-1=0
1+1+1+1-1-1-1-1=0
....
存在无限长度
所以如果允许负数出现，则必须限制排列的最大长度，避免出现无限长度的排列，才能计算排列数。

 

 

 

代码展示：

回溯的方式：

//时间0 ms击败100%
//内存38.8 MB击败45.30%
class Solution {
    private int[] nums;
    private int[] memo;
    public int combinationSum4(int[] nums, int target) {
        this.nums = nums;
        int n = nums.length;
        memo = new int[target + 1];
        Arrays.fill(memo, -1);
        return dfs(target);
    }

    public int dfs(int c){
        if(c == 0) return 1;
        if(memo[c] != -1) return memo[c];
        int cnt = 0;
        for(int i = 0;i < nums.length;i++){
            if(nums[i] <= c){
                cnt += dfs(c - nums[i]);
            }
        }
        return memo[c] = cnt;
    }
}

 

动态规划的方式：

//时间1 ms击败98.6%
//内存38.9 MB击败36.93%
//时间复杂度：O(target×n)，其中 target 是目标值，nnn 是数组 nums 的长度。
//需要计算长度为 target+1 的数组 dp 的每个元素的值，对于每个元素，需要遍历数组 nums 之后计算元素值。
//空间复杂度：O(target)。需要创建长度为 target+1 的数组 dp。
class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target+1];
        dp[0]=1;
        for(int k = 1 ; k<dp.length;k++){
            dp[k]=0;
        }
        for(int i = 1; i <= target; i++){
            for (int n : nums){
                if (n <= i) dp[i] += dp[i-n];
            }
        }
        return dp[target];
    }
}