剑指 Offer II 043. 往完全二叉树添加节点（919. 完全二叉树插入器）

题目：

 

 

 

思路：

【0】满二叉树和完全二叉树的理念

 

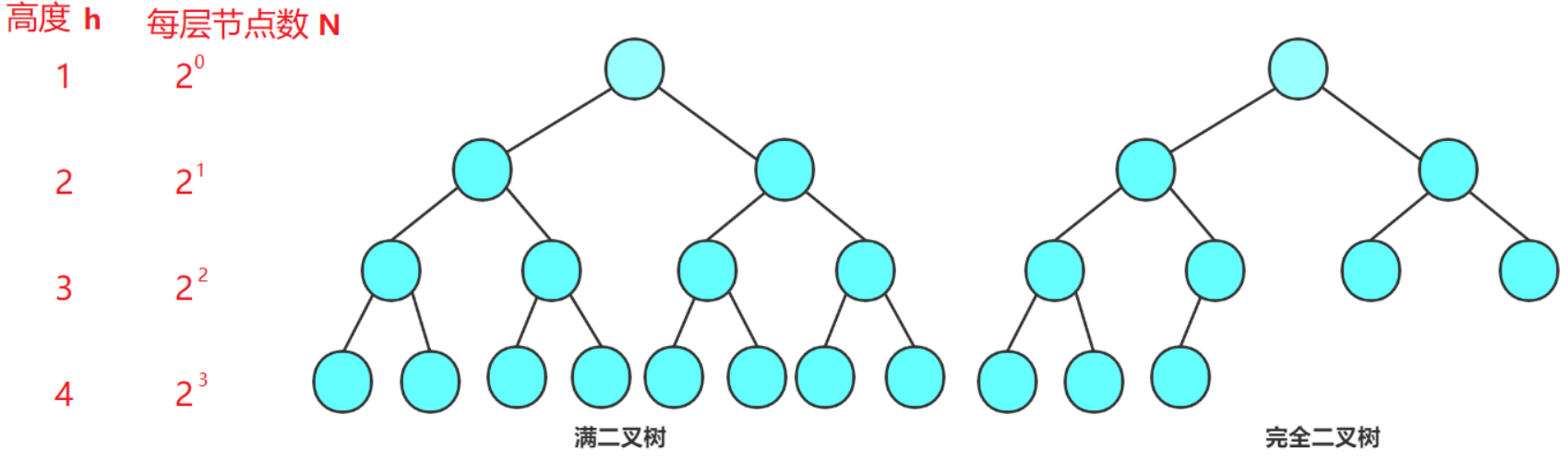
满二叉树
①所有叶子节点都在最后一层
②所有分支节点都有两个孩子

完全二叉树
①前n-1层为满的
②最后一层不满，但最后一层从左往右是连续的 

实际上若是用数组来表示
[1,2,3,4,5,6,7,8]
那么当要插入9的时候如何找到9的父节点
已知[1,2,3,4,5,6,7,8,9]下标为8
而且根据二叉树的 父节点为x，那么左子节点为2x，右子节点为2x+1
由于下标是从0开始的，那么1的左节点2下标是1，右结点3下标是2
则1/2=0,(3-1)/2=0.刚好满足(在java中整数相除不会保留小数)。
所以偶数应该先减1再除以二即可以找到父节点的下标
如(8-1)/2=3，故父节点是4

 

【1】队列的方式

【2】二进制表示的方式

代码展示：

二进制表示的方式：

//时间14 ms击败54.55%
//内存41.9 MB击败75.17%
//时间复杂度：初始化 CBTInserter(root) 需要的时间为 O(n)，其中 n 是给定的初始完全二叉树的节点个数。
//空间复杂度：初始化 CBTInserter(root) 需要的空间为 O(n)。
//如果使用优化方法，空间可以降低到 O(log⁡n)。其它所有函数调用都只需要 O(1) 的空间。
class CBTInserter {
    int cnt;
    TreeNode root;

    public CBTInserter(TreeNode root) {
        this.cnt = 0;
        this.root = root;

        Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
        queue.offer(root);
        
        while (!queue.isEmpty()) {
            ++cnt;
            TreeNode node = queue.poll();
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
    }

    public int insert(int val) {
        ++cnt;
        TreeNode child = new TreeNode(val);
        TreeNode node = root;
        int highbit = 31 - Integer.numberOfLeadingZeros(cnt);
        for (int i = highbit - 1; i >= 1; --i) {
            if ((cnt & (1 << i)) != 0) {
                node = node.right;
            } else {
                node = node.left;
            }
        }
        if ((cnt & 1) != 0) {
            node.right = child;
        } else {
            node.left = child;
        }
        return node.val;
    }

    public TreeNode get_root() {
        return root;
    }
}

 

队列的方式（重点在于，初始化的时候按层次遍历的方式，把子节点每天满的塞入到队列里面，等需要插入新节点的时候从队列拿出，如果子节点位置满了则从队列移除）：

//时间13 ms击败100%
//内存42.1 MB击败56.76%
//时间复杂度：初始化 CBTInserter(root) 需要的时间为 O(n)，其中 n 是给定的初始完全二叉树的节点个数。
//insert(v) 和 get_root() 的时间复杂度均为 O(1)。
//空间复杂度：O(n+q)，其中 q 是 insert(v) 的调用次数。
//在调用了 q 次 insert(v) 后，完全二叉树中有 n+q 个节点，其中有一半的节点在队列中，需要 O(n+q) 的空间。
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class CBTInserter {
    Queue<TreeNode> candidate;
    TreeNode root;

    public CBTInserter(TreeNode root) {
        this.candidate = new ArrayDeque<TreeNode>();
        this.root = root;

        Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
            if (!(node.left != null && node.right != null)) {
                candidate.offer(node);
            }
        }
    }

    public int insert(int val) {
        TreeNode child = new TreeNode(val);
        TreeNode node = candidate.peek();
        int ret = node.val;
        if (node.left == null) {
            node.left = child;
        } else {
            node.right = child;
            candidate.poll();
        }
        candidate.offer(child);
        return ret;
    }

    public TreeNode get_root() {
        return root;
    }
}

/**
 * Your CBTInserter object will be instantiated and called as such:
 * CBTInserter obj = new CBTInserter(root);
 * int param_1 = obj.insert(v);
 * TreeNode param_2 = obj.get_root();
 */