剑指 Offer II 066. 单词之和（677. 键值映射）

题目：

 

 

 

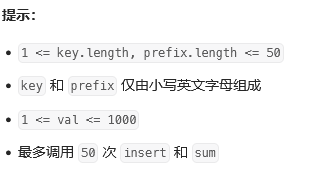
思路：

【1】暴力破解的方式

【2】前缀哈希映射的方式（这种方式和ES的原理有点相似，就是进行分词，每一个分词都叠加上对应的数据）

【3】字典树的方式

直接在前缀对应的 Trie 的每个节点存储该前缀对应的值：
1）insert 操作：原理与前缀哈希映射一样，我们首先求出前缀对应的值的改变 delta，我们直接在 Trie 节点上更新键 key 的每个前缀对应的值。
2）sum 操作: 我们直接在前缀树上搜索该给定的前缀对应的值即可，如果给定的前缀不在前缀树中，则返回 0。 
当然在实际中我们也可以在 Trie 的节点只存储键 key 对应的 val, 每次求 sum 时利用 DFS 或者 BFS 遍历前缀树的子树即可。

 

【4】说明，暴力破解在数量少的时候其实相对更快，因为其实不占用什么空间，如果说查找多的，其实理论上前缀哈希映射是最快的，因为采用的是空间换时间的本质，直接通过映射就可以拿到了，但是耗费的空间也是最多的，每个词都需要拆分而且还不能重复利用（如 ac，和ab，这两块的其实就不能有重复的部分）。而字典树的本质上是折中，节约点空间，但是拿的时候耗费的时间不如前缀哈希映射那么快，但是基于是树，其实也是指数的时间复杂度，其实也是相对很快，但是（如 ac，和ab）其实a的部分就可以用同一个节点表示，对于新加入的如果之前有的节点其实都是可以重复拿来用的。

 

代码展示：

字典树的方式：

//时间10 ms击败100%
//内存41.4 MB击败48.73%
//时间复杂度：insert 操作时间复杂度为 O(N)，其中 N 是插入的字符串 key 的长度。
//sum 操作时间复杂度为 O(N)，其中 O(N) 为给定的查询字符的长度，需要在前缀树中搜索给定的前缀。
//空间复杂度：O(CNM)，其中 M 表示 key-val 键值的数目，N 表示字符串 key 的最大长度，C 为常数。
class MapSum {
    class TrieNode {
        int val = 0;
        TrieNode[] next = new TrieNode[26];
    }

    TrieNode root;
    Map<String, Integer> map;

    public MapSum() {
        root = new TrieNode();
        map = new HashMap<>();
    }
    
    public void insert(String key, int val) {        
        int delta = val - map.getOrDefault(key, 0);
        map.put(key, val);
        TrieNode node = root;
        for (char c : key.toCharArray()) {
            if (node.next[c - 'a'] == null) {
                node.next[c - 'a'] = new TrieNode();
            }
            node = node.next[c - 'a'];
            node.val += delta;
        }
    }
    
    public int sum(String prefix) {
        TrieNode node = root;
        for (char c : prefix.toCharArray()) {
            if (node.next[c - 'a'] == null) {
                return 0;
            }
            node = node.next[c - 'a'];
        }
        return node.val;
    }
}

 

前缀哈希映射的方式：

//时间10 ms击败100%
//内存41.2 MB击败72.92%
//时间复杂度：insert 操作时间复杂度为 O(N)，其中 N 是插入的字符串 key 的长度，我们需要把字符串的所有前缀都在哈希表中插入一次。sum 操作时间复杂度为 O(1)。
//空间复杂度：O(MN)，其中 M 表示 key-val 键值的数目，N 表示字符串 key 的最大长度，由于我们需要用哈希表存储所有的 key 的前缀，每个字符串 key 最多有 N 个前缀，因此空间复杂度为O(MN)。
class MapSum {
    Map<String, Integer> map;
    Map<String, Integer> prefixmap;

    public MapSum() {
        map = new HashMap<>();
        prefixmap = new HashMap<>();
    }
    
    public void insert(String key, int val) {
        int delta = val - map.getOrDefault(key, 0);
        map.put(key, val);
        for (int i = 1; i <= key.length(); ++i) {
            //至于substring底层采用的是Arrays.copyOfRange
            String currprefix = key.substring(0, i);
            prefixmap.put(currprefix, prefixmap.getOrDefault(currprefix, 0) + delta);
        }
    }
    
    public int sum(String prefix) {
        return prefixmap.getOrDefault(prefix, 0);
    }
}

 

暴力破解的方式：

//时间10 ms击败100%
//内存41.5 MB击败33.34%
//时间复杂度：insert 操作时间复杂度为 O(1)。sum 操作时间复杂度为 O(NM)，其中 N 是插入的 key 的数目，M 是给定前缀 prefix 的长度。
//空间复杂度：O(NM)，其中 N 是插入的 key 的数目，M 是字符串 key 的最大长度。
class MapSum {
    Map<String, Integer> map;
    /** Initialize your data structure here. */
    public MapSum() {
        map = new HashMap<>();
    }
    
    public void insert(String key, int val) {
        map.put(key,val);
    }
    
    public int sum(String prefix) {
        int res = 0;
        for (String s : map.keySet()) {
            //startsWith() 方法用于检测字符串是否以指定的前缀开始
            if (s.startsWith(prefix)) {
                res += map.get(s);
            }
        }
        return res;
    }
}

/**
 * Your MapSum object will be instantiated and called as such:
 * MapSum obj = new MapSum();
 * obj.insert(key,val);
 * int param_2 = obj.sum(prefix);
 */