Python: 2D integration. Compare of rectangle, Simpson and SciPy methods 

 1 import numpy as np
 2 import matplotlib.pyplot as plt
 3 import math
 4 
 5 from mpl_toolkits.mplot3d import Axes3D
 6 
 7 xmin=-5
 8 xmax=5
 9 ymin=-5
10 ymax=5
11 N=1000
12 X=np.linspace(xmin,xmax,N)
13 Y=np.linspace(ymin,ymax,N)
14 X, Y = np.meshgrid(X, Y)
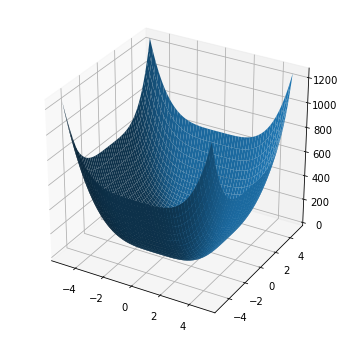
15 Z = X**4 + Y**4
16 
17 fig = plt.figure(figsize=(6,6))
18 ax = fig.add_subplot(111, projection='3d')
19 
20 # Plot a 3D surface
21 ax.plot_surface(X, Y, Z)
22 
23 plt.show()
24 
25 plt.figure()
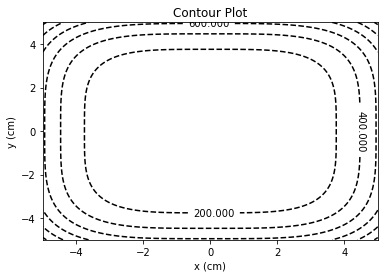
26 cp = plt.contour(X, Y, Z, colors='black', linestyles='dashed')
27 plt.clabel(cp, inline=True, 
28           fontsize=10)
29 plt.title('Contour Plot')
30 plt.xlabel('x (cm)')
31 plt.ylabel('y (cm)')
32 plt.show()

 1 for j in range(N):
 2     for i in range(0,N):
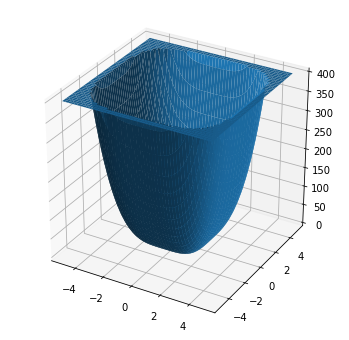
 3         if Z[i,j] > 400:
 4             Z[i,j] = 400  # replace the data greater than 400 with 400
 5             
 6 fig = plt.figure(figsize=(6,6))
 7 ax = fig.add_subplot(111, projection='3d')
 8 
 9 # Plot a 3D surface
10 ax.plot_surface(X, Y, Z)

 1 # The rectangles method
 2 vol_whole = ((xmax-xmin)**2)*400
 3 def rectangle(X,Y,N):
 4     d = X[1]-X[0]
 5     vol = 0
 6     for i in range(0,N):
 7         vol += Y[i]
 8     vol *= d
 9     return vol
10 
11 s = np.zeros(N)
12 for i in range(0,N): # integrate in x surface first
13     s[i] = rectangle(X[i,:],Z[i,:],N) # s is the surface area
14 vol = rectangle(Y[:,0],s,N) # integrate in y surface. This volume is the part under the water surface, not the water volume
15 
16 vol_true = vol_whole - vol # you should use whole volume under 400 to minus the volume under the water surface
17 print('volume by rectangle is: ', vol_true)
volume by rectangle is:  19696.675605448814
 1 # Simpson’s method
 2 def simps(X,Y,N):
 3     d = X[1]-X[0]
 4     val_a = 0
 5     val_b = 0
 6     for i in range(N):
 7         if i ==0 or i == N-1:
 8             pass
 9         else:
10             if i % 2 == 1:
11                 val_a += 4*Y[i]
12             else:
13                 val_b += 2*Y[i]
14     return (d/3)*(Y[0]+Y[N-1]+val_a+val_b)
15 
16 s = np.zeros(N)
17 for i in range(N): # integrate in x surface first
18     s[i] = simps(X[i,:],Z[i,:],N) # s is the surface area
19 vol = simps(Y[:,0],s,N) # integrate in y surface
20 
21 vol_true = vol_whole - vol
22 print('volume by Simpson is: ', vol_true)
volume by Simpson is:  19803.484672329087
 1 # SciPy
 2 import scipy.integrate as integrate
 3 
 4 vol_whole = ((xmax-xmin)**2)*400
 5 dx=X[0,1]-X[0,0]
 6 dy=Y[1,0]-Y[0,0]
 7 s=np.zeros(N)
 8 for i in range(N):
 9     s[i]=integrate.simps(Z[:,i],dx=dx)
10     Volume_Simpson=integrate.simps(s,dx=dy)
11 vol = vol_whole - Volume_Simpson
12 print('volume by Scipy is: ', vol)
volume by Scipy is:  19776.795765649047
posted @ 2020-12-19 01:44  cfdchen  阅读(151)  评论(0)    收藏  举报