人工智能
损失函数
损失函数是验证学习成果,判断预测结果是否准确。
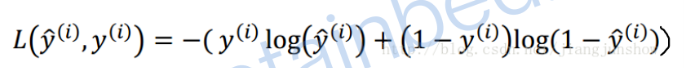
损失函数运算后得出的结果越大,那么预测就与实际结果的偏差越大,即预测精度越不高。理论上你可以用上面的公式作为损失函数。
努力使损失函数的值越小就是努力让预测的结果越准确。
成本函数
上面对单个训练样本我们定义了损失函数。下面的公式用于衡量预测算法对整个训练集的预测精度。其实就是对每个样本的“损失"进行累加,然后求平均值。这种针对于整个训练集的损失函数我们称它为成本函数(cost function)。它的计算结果越大,说明成本越大,即预测越不准确。
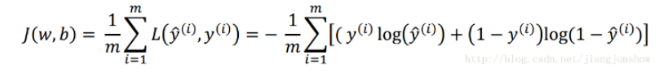
损失函数的作用就是衡量模型模型预测的好坏。再简单一点说就是:损失函数就是用来表现预测与实际数据的差距程度。换一种说法就是衡量两个分布之间的距离:其中一个分布应当是原始分布,或者正确的分布(ground truth),而另一个分布则是目前的分布,或者模型拟合的分布(prediction)。
梯度下降
在前面的文章中,我们已经知道,预测得是否准确是由w和b决定的,所以神经网络学习的目的就是要找到合适的w和b。通过一个叫做梯度下降(gradientdescent)的算法可以达到这个目的。梯度下降算法会一步一步地改变w和b的值,新的w和b会使损失函数的输出结果更小,即一步一步让预测更加精准。
逻辑回归: z = dot(w,x) + b= (x1 * w1 + x2 * w2 + x3 * w3) + b。
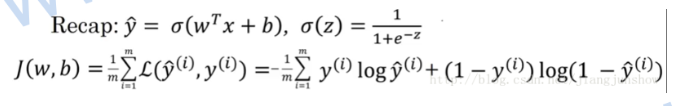
上面的公式是我们之前学到的逻辑回归算法(用于预测),以及损失函数J (用于判断预测是否准确)。结合上面两个公式,输入x 和实际结果 y 都是固定的,所以损失函数其实是一个关于w和b的函数(w和b是变量)。所谓"学习"或“训练神经网络",就是找到一组w和b,使这个损失函数最小,即使预测结果更精准。

w' = w - r * dw
梯度下降算法就是重复的执行上面的公式来不停的更新w的值。新的w的值(w')等于旧的w减去学习率 r 与偏导数 dw 的乘积。
计算图
一个人工智能学习任务的核心是模型的定义以及模型的参数求解方式,对这两者进行抽象之后,可以确定一个唯一的计算逻辑,将这个逻辑用图表示,称之为计算图。计算图表现为有向无环图,定义了数据的流转方式,数据的计算方式,以及各种计算之间的相互依赖关系等。
神经网络的计算是由一个前向传播以及一个反向传播构成的。先通过前向传播计算出预测结果以及损失; 然后再通过反向传播计算出损失函数关于每一个参数(w、b)的偏导数,并对这些参数进行梯度下降,然后用新的参数进行新一轮的前向传播计算,这样来回不停地进行前向传播反向传播计算来训练(更新)参数使损失函数越来越小使预测越来越精准。
1.2.6 计算逻辑回归的偏导数
逻辑回归前向传播
如下图所示,在逻辑回归的前向传播过程中,第一步我们要先计算出z,第二步计算出预测值y或a,最后计算出损失函数L。(下图中假设只有两个特征 x 和 x2 )
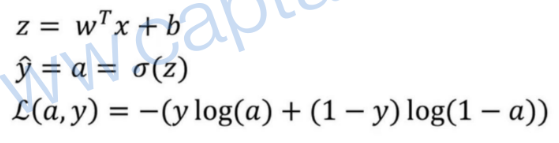
如何求反向传播?
1.求dL/da = -(y/a)+(1-y)/(1-a)
2.求dL/dz = dL/da * da/dz = -(y/a)+(1-y)/(1-a) * a(1-1)= a-y
3.dw1 = x1dz, dw2=x2dz, db = dz。
w1' = w1 - r * dw1,
1.2.7向量化

上面这段代码中最关键的一行是 np.dot(A, B.T)。dot 执行了一个向量乘法运算,等价于上面的循环代码。
向量化人工智能算法

w之前是一个列向量,转置后成为行向量。x(i) 列向量 。

特征工程
1.多热编码
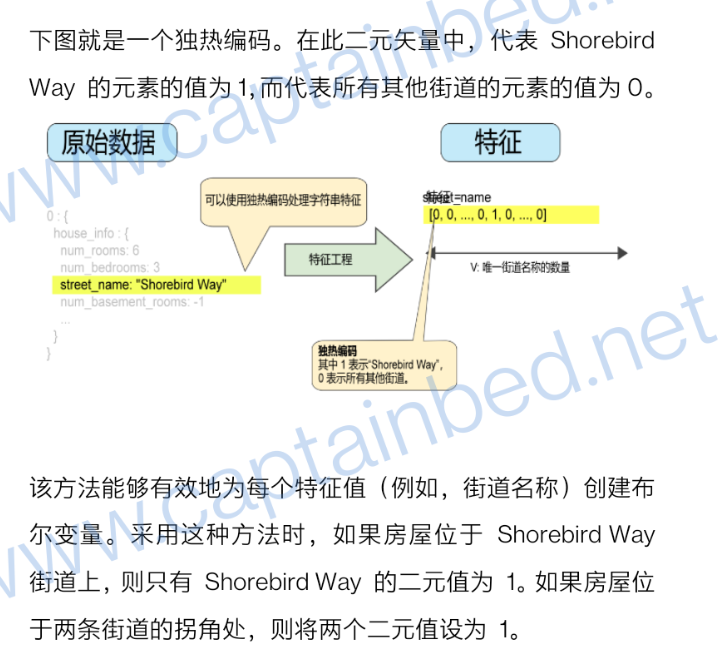
2.稀疏表示法
一个特征向量,其中的大多数值都为О或为空。例如,某个向量包含一个为1的值和一百万个为О的值,则该向量就属于稀疏向量,反之就是密集向量。
下面我们以上面两种方式来表示句子“Dogs wag tails."。如下表所示,密集表示法将使用约一百万个单元格;稀疏表示法则只使用3个单元格:
|
单元格编号(密集表示法) |
单词 | 出现次数 |
| 0 | a | 0 |
| 1 | ... | 0 |
| 2 | dogs | 1 |
| 3 | wag | 1 |
| 4 | tails | 1 |
| 1000000 | ... | 0 |
| 单元格编号(稀疏表示法) | 单词 | 出现次数 |
| 140899 | dogs | 1 |
| 162876 | wag | 1 |
| 982136 | tails | 1 |
浅层神经网络
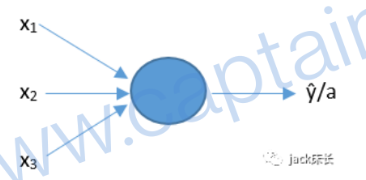
上面这个唯一的神经元,其实负责执行了如下运算。
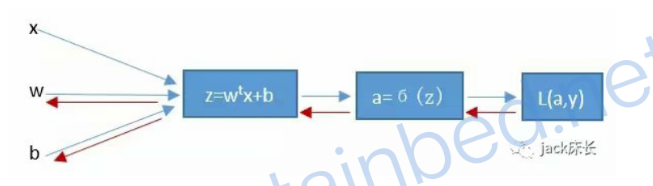
这个神经元通过对x, w,b进行运算,得出z,然后再由z得出a。
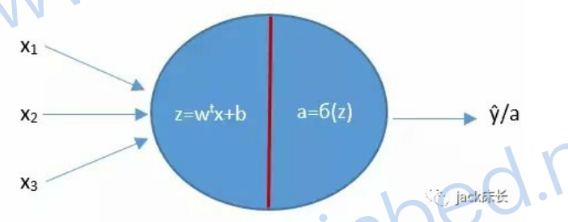
a就是预测结果,我们通过a和真实的标签y就可以构建一个损失函数L来计算出损失。同时我们可以从损失函数开始反向传播回到这个神经元来计算出w和b相对于损失函数的偏导数/梯度,以便进行梯度下降,然后再次进行前向传播,这样不停地反复来优化w和b...




 浙公网安备 33010602011771号
浙公网安备 33010602011771号